电容式传感器的特点及工作原理解析

1 引言

用电测法测量非电学量时，首先必须将被测的非电学量转换为电学量而后输入之。通常把非电学量变换成电学量的元件称为变换器；根据不同非电学量的特点设计成的有关转换装置称为传感器，而被测的力学量（如位移、力、速度等）转换成电容变化的传感器称为电容传感器。

从能量转换的角度而言，电容变换器为无源变换器，需要将所测的力学量转换成电压或电流后进行放大和处理。力学量中的线位移、角位移、间隔、距离、厚度、拉伸、压缩、膨胀、变形等无不与长度有着密切联系的量;这些量又都是通过长度或者长度比值进行测量的量，而其测量方法的相互关系也很密切。另外，在有些条件下，这些力学量变化相当缓慢，而且变化范围极小，如果要求测量极小距离或位移时要有较高的分辨率，其他传感器很难做到实现高分辨率要求，在精密测量中所普遍使用的差动变压器传感器的分辨率仅达到1～5 μm数量级;而有一种电容测微仪，他的分辨率为0.01 μm，比前者提高了两个数量级，最大量程为100±5 μm，因此他在精密小位移测量中受到青睐。

对于上述这些力学量，尤其是缓慢变化或微小量的测量，一般来说采用电容式传感器进行检测比较适宜，主要是这类传感器具有以下突出优点：

（1）测量范围大其相对变化率可超过100%;

（2）灵敏度高如用比率变压器电桥测量，相对变化量可达10-7数量级;

（3）动态响应快因其可动质量小，固有频率高，高频特性既适宜动态测量，也可静态测量;

（4）稳定性好由于电容器极板多为金属材料，极板间衬物多为无机材料，如空气、玻璃、陶瓷、石英等;因此可以在高温、低温强磁场、强幅射下长期工作，尤其是解决高温高压环境下的检测难题。

2 原理及应用

电容传感器的工作原理是利用力学量变化使电容器中其中的一个参数发生变化的方法来实现信号变换的。根据改变电容器的参数不同，电容传感器可有3类：

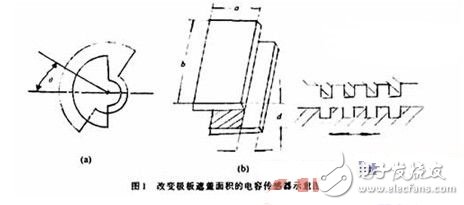
2.1 改变极板遮盖面积的电容传感器

图1是3种这类传感器的原理图，图1（a）中是利用角位移来改变电容器极板遮盖面积。假定当2块极板完全遮盖时的面积为S0，两极板间的距离为d，极板间介质的介电常数为ε。当忽略边缘效应时，该电容器的电容量为：

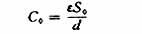
如果其中一块板极相对另一极板转过θ角，则极板间的相互遮盖面积为：

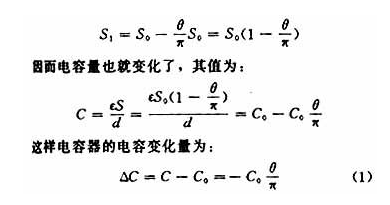
可见，此电容量的变化值和角位移成正比，以此用来测量角位移。

图1（b）中是利用线位移来改变电容器极板的遮盖面积的。如果初始状态极板全部遮盖，则遮盖面积S0=ab，当2块极板相对位移x时，则极板的遮盖面积变为S1=b（a-x）。在介电常数和极板距离不变时，电容量分别为：

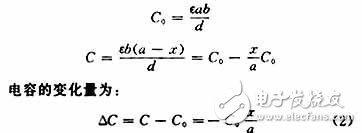
可见，此电容量的变化值和线位移x成正比，用他来测量各类线位移。

图1（c）所示电容变换器是图1（b）所示电容器的变种。采用这种锯齿形电极的目的在于提高传感器的灵敏度。若锯齿数为n，尺寸如图1（b）所示不变，当运动齿相对于固定齿移动一个位移x时，则可得：

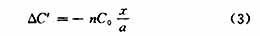
比较式（2）和式（3）可见，灵敏度提高了n倍。

2.2 改变介质介电常数的电容传感器

图2是2种改变介质介电常数的电容式传感器的原理图。图2（a）常用来检测液位的高度，图2（b）常用来检测片状材料的厚度和介电常数。

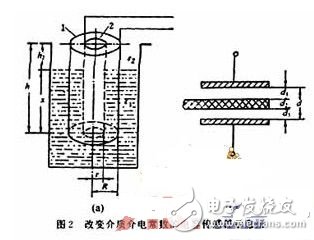
图2（a）中由圆筒1和圆柱2构成电容器两极，假定部分浸入被测量液体中（液体应不能导电，若能导电，则电极需作绝缘处理）。这样，极板间的介质由2部分组成：空气介质和液体介质，由此而形成的电容式料位传感器，由于液体介质的液面发生变化，从而导致电容器的电容C也发生变化。这种方法测量的精度很高，且不受周围环境的影响。总电容C由液体介质部分电容C1和空气介质部分电容C2两部分组成：

x — 电容器浸入液体中的深度;

R — 同心圆电极的外半径;

r — 同心圆电极的内半径;

ε1 — 被测液体的介电常数;

ε2 — 空气的介电常数。

当容器的尺寸和被测介质确定后，则h，R，r，ε1和ε2均为常数，令：

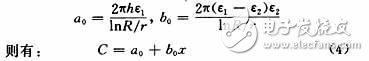
这说明，电容量C的大小与电容器浸入液体的深度x成正比。

图2（b）是在一个固定电容器的极板之间放入被测片状材料，则他的电容量为：

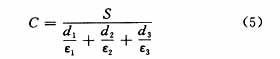
式中：S — 电容器的遮盖面积;

d1 — 被测物体上侧至电极之间的距离;

d2 — 被测物体的厚度;

d3 — 被测物体下侧至电极之间的距离;

ε1 — 被测物体上侧至电极之间介质的介电常数;

ε2 — 被测物体的介电常数;

ε3 — 被测物体下侧至电极之间介质的介电常数。

由于d1+d3=d-d2，且当ε1=ε3时，式（5）还可写为：

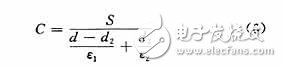
式中d — 两极板之间的距离。

显然，在电容器极板的遮盖面积S，两极板之间的距离d，被测物体上下侧至电极之间介质的介电常数ε1和ε3确定时，电容量的大小就和被测材料的厚度d2及介电常数ε2有关。如被测材料介电常数ε2已知，就可以测量等厚教材料的厚度d2;或者被测材料的厚度d2已知，就可测量其介电常数ε2。这就是电容式测厚仪和电容式介电常数测量仪的工作原理。

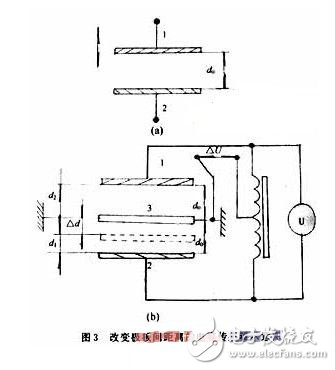
3改变极板间距离的电容传感器

图3是这类传感器的原理图，图3（a）由2块极板构成，其中极板2为固定极板，极板1为与被测物体相连的活动极板，可上下移动。当极板间的遮盖面积为S，极板间介质的介电常数为ε，初始极板间距为d0时，则初始电容C0为：

当活动极板1在被测物体的作用下向固定极板2位移Δd 时，此时电容C为：

当电容器的活动极板1移动极小时，即Δd《

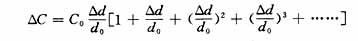
这时电容器的变化量ΔC才近似地和位移Δd成正比。其相对非线性误差为：

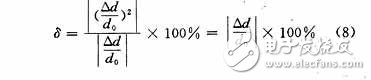
显然，这种单边活动的电容传感器随着测量范围的增大，相应的误差也增大。在实际应用中，为了提高这类传感器灵敏度、提高测量范围和减小非线性误差，常做成差动式电容器及互感器电桥组合结构，如图3（b）所示。两边是固定的电极板1和2，中间由弹簧片支承的活动极板3。2个固定极板与互感器两端及交流电源U相连接，活动极板连接端子和互感器中间抽头端子为传感器的输出端，该输出端电压ΔU随着活动极板运动而变化。若活动极板的初始位置距2个固定极板的距离均为d0，则固定极板1和活动极板3之间 ，固定2和活动极板3之间的初始电容相等，若令其为C0。当活动极板3在被测物体作用下向固定极板2移动Δd时，则位于中间的活动极板到两侧的固定极板的距离分别为：

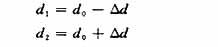
由上述推导可知，活动极板和2个固定极板构成电容分别为：

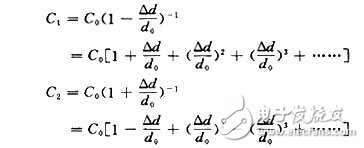
当他们做成差动式电容器及互感器电桥组合结构时，其等效电容为：

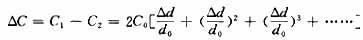
虽然电容的变化量仍旧和位移Δd成非线性关系，但是消除了级数中的偶次项，使线性得到改善。当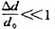时（在微小量检测中，如线膨胀测量等，一般都能满足这个条件），略去高次项，得：

比较式（9）和式（7）可见，灵敏度提高了1倍。

比较式（10）和式（8）可见，在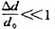1时，非线性误差将大大下降。