

执行节点分析时的特殊情况介绍
描述
当我们在设计电子威廉希尔官方网站 时,了解流过元件的电流量或威廉希尔官方网站 中特定节点在其工作的关键点存在多少电压始终是很重要的。使用基尔霍夫威廉希尔官方网站 定律可以完成任一测量。允许我们找到这些值的两种分析类型是网格分析和节点分析。如果我们试图在一个点(节点)找到电压,那么我们可以使用基尔霍夫电流定律(KCL)进行节点分析。
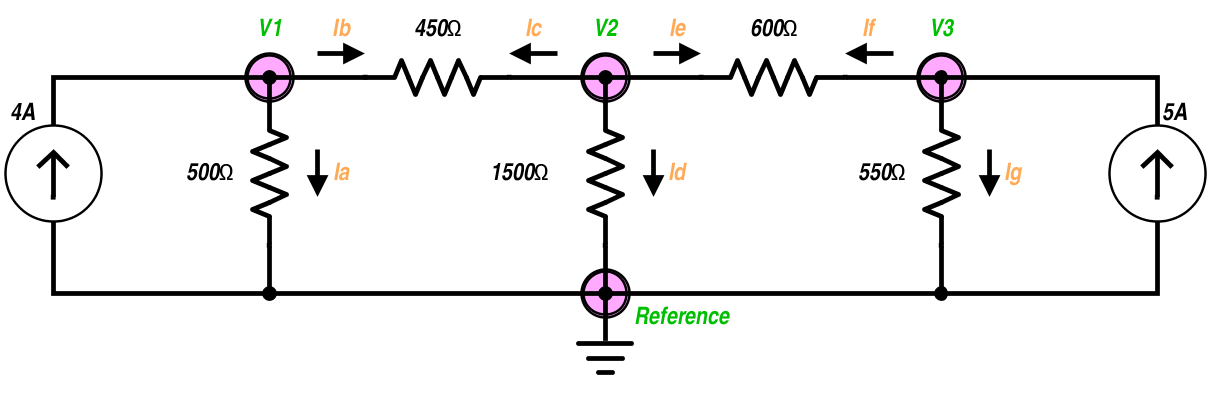
此原理图中的每个特定节点(V1,V2和V3)都有3个连接。 KCL声明每个节点的所有分支电流之和为零。我们可以用它来通过以下方法找到每个节点的电压:
首先,我们有一个具有最低电位的参考节点,称为地。选择该威廉希尔官方网站 中的地是因为它是具有最低电压的共同点。接下来,我们为每个电压未知的节点分配一个变量。这由V1,V2和V3处的圆圈标记。第三,应用KCL形成每个未知电压的等式。
对于节点V1:
电流Ia和Ib :
$$ Ia $$ = $$ \ frac {V1} {500Ω} $$和$$ Ib = \ frac {(V1-V2)} {450Ω} $$
这是因为通过电阻器的电压是两个节点之间的电位差。由于V1是唯一直接连接到4安培电流源的节点,因此$$ Ia + Ib = 4安培$$。
将所有这些放在一起:
$$ \ frac { V1} {500Ω} + \ frac {(V1-V2)} {450Ω} = 4安培$$。
这可以改写为:
$$ V1(\ frac) {1} {500Ω} + \ frac {1} {450Ω}) - V2(\ frac {1} {450Ω})= 4安培$$。
对于节点V2:
Ic从V2指向V1,因此我们将450Ω电阻分支写为:$$ \ frac {(V2-V1)} {450Ω} $$。
Id简单地说:$$ \ frac {V2} {1500Ω} $$。
即从V2流向V3并记为:$$ \ frac {(V2-V3)} {600Ω} $$。
请记住,KCL要求所有3个分支的总和为零。这意味着$$ Ic + Id + Ie = 0 $$。
作为一个公式,它被组合为:
$$ \ frac {(V2-V1)} { 450Ω} + \ frac {V2} {1500Ω} + \ frac {(V2-V3)} {600Ω} = 0 $$。
线性方程的一个更友好的形式是:
$$ - V1(\压裂{1} {450})+ V2(\压裂{1} {450} + \压裂{1} {1500} + \压裂{1} {600}) - V3(\ frac {1} {600})= 0 $$。
节点V3与节点V1的结构相同,只有不同的值。
Ig是:$$ \ frac { V3} {550Ω} $$。
如果(eye-eff,而不是iff。英语嘲笑我们!)是:$$ \ frac {(V3-V2)} {600Ω} $$。
两个电阻都来自5安培电流源,使得If If + Ig = 5 A $$。
放在一起,我们有:
$$ \ frac {(V3-V2)} {600Ω} + \ frac {V3} {550Ω} = 5 A $$。
为计算而兴奋,等式为:
$$ - V2(\压裂{1} {600})+ V3(\压裂{1} {550} + \压裂{1} {600})= 5 $$
第四步也是最后一步是解决方程组。有计算器可以解决线性方程组。 Matlab和GNU Octave是可以执行此功能的PC程序。用铅笔,纸和20分钟的时间;我们可以用代数解决这个“老派”。然而,我们不妨使用更快,更可靠的方法,所以让我们选择www.wolframalpha.com的在线选项。
我们的三个最终方程可以组合在一起:
$$ v1(\ frac {1} {500} + \ frac {1} {450} - v2(\ frac {1} {450})= 4 $$,
$$ - v1(\ frac {1} {450})+ v2(\ frac {1} {450} + \ frac {1} {1500} + \ frac {1} {600}) - v3(\ frac {1} { 600})= 0 $$,
$$ - V2(\压裂{1} {600})+ V3(\压裂{1} {550} + \压裂{1} {600}) = 5 $$。
虽然这在数学上是正确的,但WolframAlpha基本上回复了“呵呵”。
为了使公式更加合适,让我们用“*”代替乘法:
$$ v1 *(\ frac {1} {500} + \ frac {1} {450} -v2 *(\ frac {1} {450})= 4 $$,
$$ - v1 *(\ frac {1} {450})+ v2 *(\ frac {1} {450} + \ frac {1} {1500} + \ frac {1} {600 }) - v3 *(\ frac {1} {600})= 0 $$,
$$ - v2 *(\ frac {1} {600})+ v3 *(\ frac {1 } {550} + \ frac {1} {600})= 5 $$。
解决方案有点乱,因为
$$ \ underline {v1 = \ frac { 3159000} {1697}} $$。
但是点击网页上的近似表格e将产生:
$$ \ underline {v1 = 1,861.5} $$,$$ \ underline {v2 = 1,736.9} $$和$$ \ underline {v3 = 2,265.5} $$。
要检查这一点,请将从两个电源流入威廉希尔官方网站 的功率与电阻器消耗的功率进行比较。节点V1具有1,861.5伏特,4安培等于7,446瓦特。在5安培时,电压为2,265.5伏,节点V3的功率为11,327.5瓦。电阻器以下列速率产生热量:450Ω34.5瓦,500Ω6,930.36瓦,1500Ω2011.21瓦,600Ω467.7瓦,550Ω9,331.8瓦。功率为18,773.5瓦。由于四舍五入问题,功耗为18,773.57瓦。要么我们设计了世界上最强大的烤箱,要么我们的电流应该少一点这个例子!
特殊情况:电压源和超级节点。
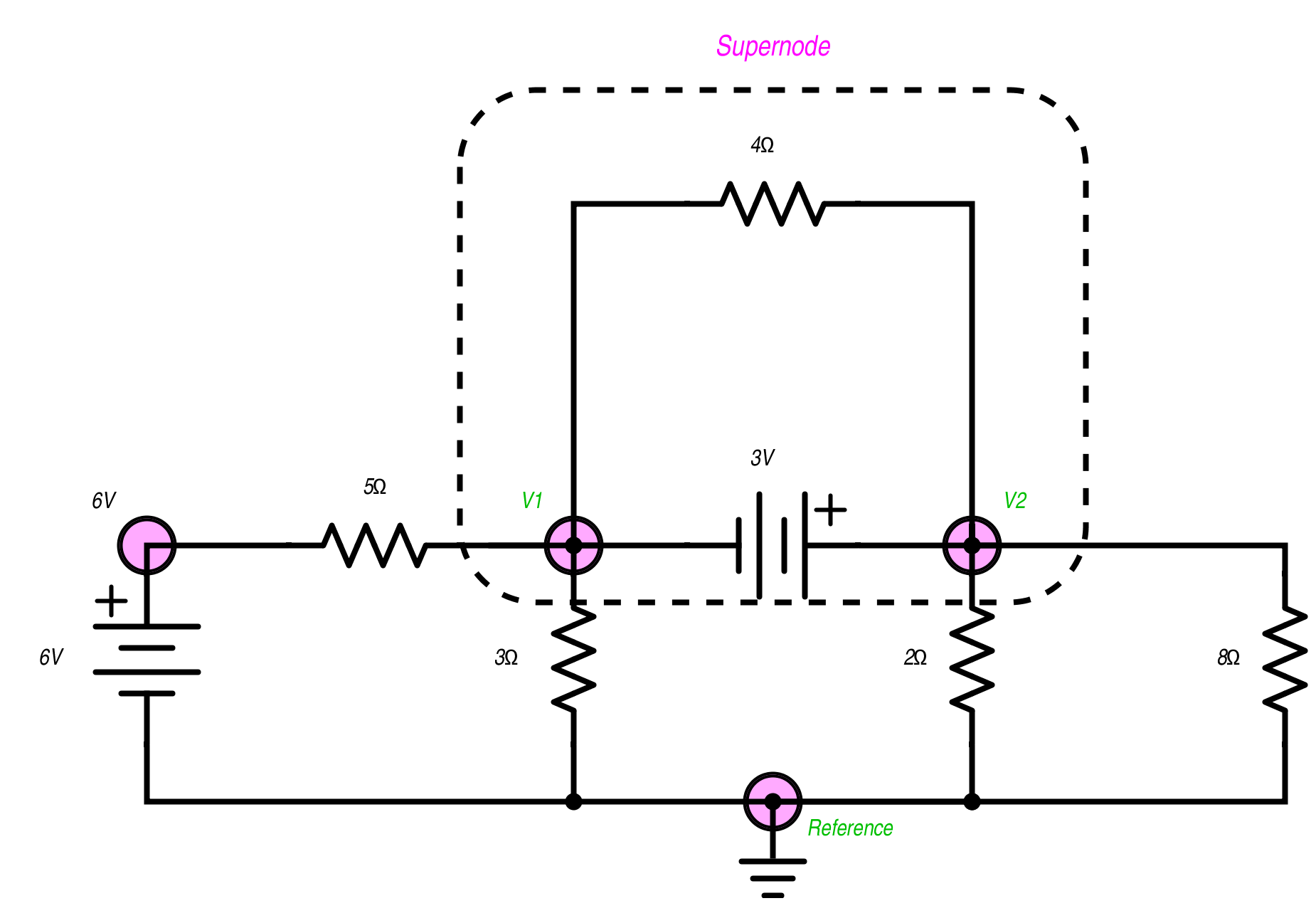
增加电压源是一种特殊情况。这里我们有一个6伏电源和3伏电源。 3伏电源位于两个非参考节点之间,形成一个超级节点。
查找参考节点的过程与上一个例子中的过程相同。
现在情况有所改变位。 6V节点不需要KCL,因为我们已经知道该位置的威廉希尔官方网站 是6伏。超级节点没有它看起来那么糟糕,我们只需要添加一个KVL方程。 3伏电池的V2侧具有比V1侧更高的电压电位,因此我们将使用的KVL是$$ V2-V1 = 3V $$。
其余威廉希尔官方网站 的KCL是:
$$ \ frac {(V1-6v)} {5Ω} + \ frac {V1} {3Ω} + \ frac {V2} {2Ω} + \ frac {V2} {8Ω} = 0 $$。
您可能已经注意到此示例中的数学运算并不那么混乱。我们选择除以阻力而不是乘以倒数。无论哪种方式都是完全有效的。
嘿! 4Ω电阻怎么样?没有人想被排除在外!那么,4Ω电阻是封装协议的一部分。它被视为超级节点的一部分,不必作为单独的等式考虑在内。幸运的是我们!
我们可以在线性方程中添加一些括号,使事情更加清晰,并将它们输入到WolframAlpha页面中:
$$ v2-v1 = 3 $$,$$ \ frac {(v1-6)} {5} + \ frac {(v1)} {3} + \ frac {(v2)} {2} + \ frac {(v2)} {8} = 0 $$。
瞧,我们发现:$$ \ underline {V1 = -0.5827} $$和$$ \ underline {V2 = 2.4173} $$作为我们的答案。
尽管看起来很复杂,节点分析是许多威廉希尔官方网站 仿真程序的基础,也是理解威廉希尔官方网站 中交叉点电压的基石。
- 相关推荐
- 元件
- 电子威廉希尔官方网站
-
#硬声创作季 威廉希尔官方网站 分析与测试:2-4.2特殊情况下节点电压方程的列写方法Mr_haohao 2022-10-28
-
电工技术: 节点电压法的特殊情况之一#电工学习电子 2022-11-13
-
电工技术: 节点电压法的特殊情况之三#电工学习电子 2022-11-13
-
电工技术: 节点电压法的特殊情况之二#电工学习电子 2022-11-13
-
回路电流法特殊情况分析处理(2)#威廉希尔官方网站未来加油dz 2023-09-04
-
节点电压法特殊情况分析处理#威廉希尔官方网站未来加油dz 2023-09-04
-
节点电压法特殊情况分析处理2(1)#威廉希尔官方网站未来加油dz 2023-09-04
-
节点电压法特殊情况分析处理2(2)#威廉希尔官方网站未来加油dz 2023-09-04
-
节点电压法特殊情况分析处理3#威廉希尔官方网站未来加油dz 2023-09-04
-
Zigbee在大数量节点应用中的问题研究2009-05-26 475
-
执行机构和定位驱动器介绍2017-10-24 663
-
Dropout如何成为SDR的特殊情况2018-08-15 3787
-
在特殊情况下,封装压电陶瓷可倒置使用2020-09-10 776
-
什么情况下不能用节点电压法2024-08-06 1028
全部0条评论

快来发表一下你的评论吧 !

