

PCB传输线中的共模信号是怎么回事
描述
本文是我们差分对系列的第一部分。它由我们的设计和装配部门总经理Atar Mittal撰写。
在第一部分中,我们将讨论:
- 单端线
- 差分对线
- 耦合系数
- 差分和共模信号
- 差分和奇数模式信号
单端线
在我们的PCB传输线系列中,我们确定单端传输线可以建模如下:
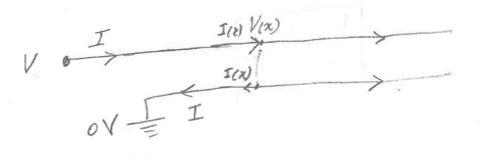
之间的关系线上任何一点的电压和电流由下式给出:
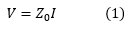
其中'Z0'是线路的特征(或瞬时)阻抗。对于无损或几乎无损的线,我们看到'Z0'由下式给出:

其中'L0'和'C0'分别是线的每单位长度(pul)的电感和电容。
差分对线
一对线可以建模如下:
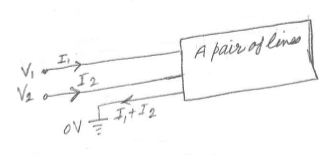
我们在此假设该对的两条线是相同且均匀的。并且它们在整个生产线上具有相同的分离。这些正是指定为差分对的一对线的特性。
当我们有一对彼此靠近的线时,可以说在线存在电流2将在线路1中感应出一些电压,线路1中的电流将在线路2中感应出一些电压。因此,线路1的电压'V1'不仅取决于线路1中的电流'I1'(通过阻抗'Z0')第1行)。它还将依赖于线2中的电流'I2'通过线1和线2之间的耦合或互阻'Zm'。这种情况可以用下面的等式表示:

其中'Zse'是第1行的特征阻抗,'Zm'是第1行和第2行之间的相互或耦合阻抗。
两条线之间的耦合
类似于第2行(差分对),与第1行相同,我们可以写出以下等式:/p>

互阻抗'Zm'是由于两条线之间的耦合而产生的。最重要的耦合剂是'Lm',互感脉冲和'Cm',第1和第2行之间的突变电容脉冲。
更紧密的是两条线相互连接,耦合更大它们之间。实际上,如果线之间的间隔'S'减小,则所有三个参数的值 - 'Lm','Cm'和'Zm' - 增加。
等式(3)和( 4)对于线1上的任何点和线2上的对应点都是如此。对于均匀的差分对,'Zse'和'Zm'在差分对的每个位置具有相同的值。
耦合系数
由于'Zm'提供从一条线耦合到另一条线的信号电压的大小,对于通过其自己的'Zse'贡献的信号,我们可以将比率'Zm/Zse'定义为差分对的两条线之间的耦合系数:

差分和共模信号
奇数和偶数模式
让'V1'和'V2'成为信号电压和'I1'和'I2'是差分对的两条线中的信号电流,其特征在于阻抗'Zse'和'Zm'。我们知道这六个量通过等式(3)和(4)相关。
信号电压'V1'和'V2'的差异称为差分信号'Vdiff'。其中一半也称为奇模式信号:

'V1'的平均值'V2'称为共模信号'Vcom'。它也被称为偶模式信号:

从5和6开始,我们可以用'Vdiff'表示'V1'和'V2' 'Vcom'如下:

这些等式表示任意两个任意信号值的普遍事实'V1'和'V2'总是表示为并因此根据公共(或偶数)模式信号和差分(或奇数)模式信号进行分析。
此外,等式(7a) (7b)还允许我们认为'V'或'V''中'V'或'V''信号的一部分是“偏置”,差分模式(或奇数模式)信号'+ Vodd'和'-Vodd'骑行导致'V1'和'V2'。这种观点是差分信号分析最重要的方面。
传播时变信号
此时,我们继续进行概念分析,让我们记住,使用传输线 - 单端或差分 - 是将时变信号 - 通常是高速数字信号或高频模拟信号 - 从一个地方传播到另一个地方。它是构成信息的时变信号。静态电压和电流没有任何信息。
因此,看看上面的等式(7a)和(7b),我们需要强调'Vcom'(或'Veven')只是一种偏见差分对的两条线上的电压。主信号是差分信号('V1-V2')。其中一半添加到第1行,通常称为正线。它由信号名称中的后缀“+”或“P”标识。从线2中减去另一半,通常称为负线,并在其上的信号名称中用后缀' - '或'N'标识,以在信号发送器端构成'V1'和'V2'。
目的地
在目的地,两条线路进入差分接收器的输入端,检测到差异('V1 - V2')在两条线上的信号幅度作为真实信号。因此,在此过程中拒绝任何共模信号 - 故意交流偏压和/或共模噪声。
这种抑制共模信号的能力以及差分信号中的任何共模噪声使其远远优越单端信令,没有办法将噪声与实际信号分开。
说完这个,我们可能会认为我们需要更深入地分析差分或奇数模式忽略共同模式。但是,我们不要忘记,当信号在线路上传播时,它们会怀疑各种噪声会叠加在它们上面。这可能会不利地影响信号完整性。因此,虽然差分对线对信号的差分(即奇数)部分的响应是我们主要关注的问题,但我们还必须分析差分对对公共(或偶数)模式信号的响应。
差分和奇数模式信号
我们现在将分析差分对,当我们只发送奇数模式信号时 - 没有任何共同点模式部分。
在这种情况下,由于'Vcom = Veven = 0',我们来自(7a)和(7b):

由于这些行是相同的,我们将'I2 = -I'使'I1 + I2 = 0'。因此,返回路径中的电流将为零。
等式(3)或(4)现在给出:

我们像往常一样,将'Vodd/Iodd'的比率定义为线的奇模阻抗:

现在'Zm = K.Zse'其中'K'是耦合系数。
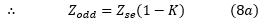
由此可见,奇模阻抗小于单线的单端阻抗'Zse'且大于'Zm'(或“两对”之间的耦合),'Zodd'与'Z0'的关系较小。
在下一篇文章中,我们将讨论差分阻抗和偶数或共模。
- 相关推荐
- pcb
- 华强pcb线路板打样
-
PCB信号传输线的特性阻抗控制2012-03-31 0
-
信号传输线及其特性阻抗2018-02-08 0
-
PCB传输线参数2018-09-03 0
-
PCB传输线之SI反射问题的解决2018-09-21 0
-
PCB传输线原理2018-11-23 0
-
什么是传输线?PCB的传输线结构是如何构成的?2021-06-29 0
-
高速PCB设计中传输线的概念及结构分析2019-12-16 6981
-
你知道pcb的传输线是怎么回事吗2020-02-28 2730
-
高速PCB设计中传输线你都有了解吗2019-12-17 3287
-
PCB传输线原理_PCB传输线参数2020-03-12 3650
-
PCB板上多长的走线才是传输线?2020-11-06 5982
-
pcb的传输线结构分析方法2023-08-04 541
-
传输线的类型有哪些?PCB上什么样的线才是传输线?2023-09-28 3807
-
什么是传输线?什么是信号完整性分析?为什么传输线要测试差分信号?2023-10-23 807
-
PCB的传输线结构2024-01-15 412
全部0条评论

快来发表一下你的评论吧 !

