

PCB传输线中的差分对是怎样的一情况
描述
在查看差分阻抗以及偶数或共模之后,我们现在深入研究差分对的物理参数。
我们将讨论:
线路电感和电容
案例1:奇数模式
案例2:偶数模式
单端阻抗
两个串扰相关参数
差分对的详细分析线电感和电容的分析
使用以下威廉希尔官方网站 模型对无损单端传输线进行分析,得到无穷小的长度'delta x':

这里,'L'和'C'分别是线路每单位长度的电感和电容。经过分析,我们得出一条点的线的特征(或瞬时)阻抗由下式给出:
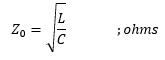
传播延迟'Pd '给出了:
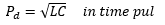
我们现在可以将上述模型和结果应用于差分对线路的电感和电容分析参与其中。我们假设这样的线条使得导体电阻('R'')和介电电导('G'')可以忽略阻抗和传播延迟的目的。这将是感兴趣的实际频率的情况。
下图给出了差分对线的无限小长度的威廉希尔官方网站 模型:
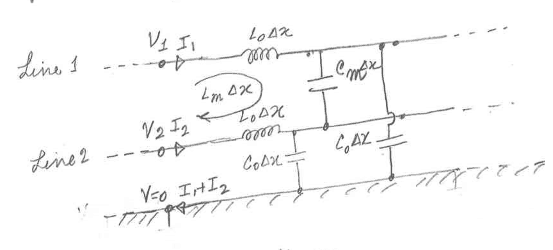
这里'L0'和'C0'分别取决于每单位长度每条线的电感和电容。 'Lm'是第1行和第2行之间每单位长度的互感。'Cm'是第1行和第2行之间每单位长度的电容。
情况1:奇数模式(纯差分信号)
这里'V2 = -V1'和'I2 = -I1'。因此,没有电流在返回路径中流动。 'Cm delta x'可以被认为是两个电容器,每个电容器的值为“2Cm delta x”,其中心点为零电位。 (这是因为两个相等电容之间的电位分压。)因此,奇数模式下的等效威廉希尔官方网站 变为:
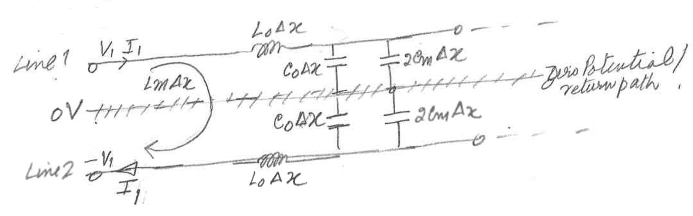
让我们来看看线路1(第2行情况完全相似)。
第1行的感应电压由两部分组成。一个归因于'I',流过'L0 delta x'。另一个是由于'I2 = -I1',流过'Lm delta x'。这些可以等效地表示为由于'I',流过'(L0-Lm)delta x'。因此,奇数模式中线1的每单位长度的有效电感,由'Lodd'表示,将由下式给出:
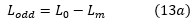
有效电容在第1行和零电位线之间是'(C0 + 2Cm)delta x'。因此,每单位长度的奇模线电容是:
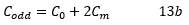
根据定义,类似于在单端线的情况下得到的结果,奇模特征阻抗由下式给出:
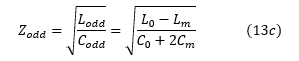
奇模信号的每单位长度传播延迟由下式给出:
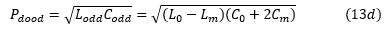
这是纯单位信号差分部分的单位长度传播延迟。此处还要记住的是,奇数模式或纯差分信号的电磁波主要存在于两条线之间的空间内和周围。并且它们受参考或地平面的影响相对较小。
情况2:偶模式(纯共模信号)
在这种情况下,'V2 = V1'并且由于该对中的两行是相同的,'I1 = I2'。由于'V1 = V2',两条线之间的电容'Cm'对两条线中的电流没有影响。因此可以忽略它,导致以下等效威廉希尔官方网站 :
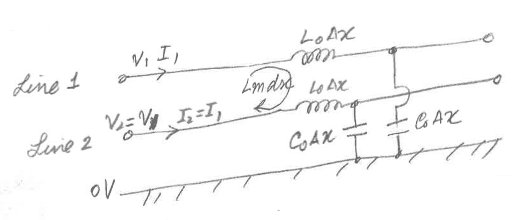
让我们看一下第1行(第2行的情况相同)。
第1行的感应电压将由'I1'贡献,流入'L0 delta x'。并且通过'I2 = I1'',流入'Lm delta x'。这相当于说'I1'流过'(L0 + Lm)delta x'。因此,偶数模式下任一行的每单位长度的有效电感将为:
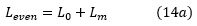
均匀模式下任一行的每单位长度有效电容将是:

因此,任一行的偶模阻抗将由下式给出:
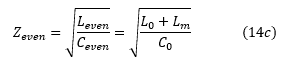
偶模信号的每单位长度的传播延迟由下式给出:
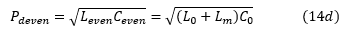
等式(13c)和(14c)清楚地表明' Zeven'比'Zodd'更重要。从理论上讲,还知道'Lm'小于'L0','Cm'小于'C0'。
'Zse ','Zm'和'K'用'L0','C0','Lm','Cm'
使用等式(12),(13)和(14) ),我们有:
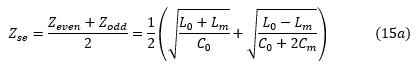
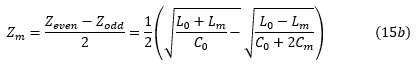
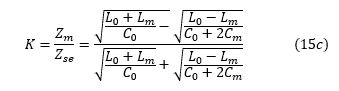
关于'Zse'的一些词
'Zse'是存在两条线的任一条中的单端阻抗另一条线。当没有第二条线时,它与单条线的单端阻抗不完全相同。第二条线的存在稍微降低了阻抗。两条线越耦合(或越接近),'Zse'将变得更少。
重要的是要注意,如果两条线之间的耦合是'Zse',则变化不大。不高。或者,如果我们可以使两条线之间的间隔大于信号层和最近的地面/参考平面之间的导体宽度或介电高度的最大值。
。如果间隔大于信号层和最近参考平面之间的介电高度,则“Zse”相对相同。
此外,'Zse'不接近'L0/C0'但更接近'L0/(C0 + Cm)'。乍一看似乎令人惊讶,但情况确实如此。
定义一些新术语并不合适:
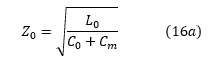
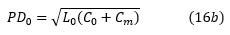
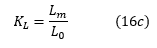
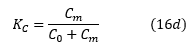
'KL'和'KC'可以分别称为电感和电容耦合系数。使用这些,我们可以将等式(15)写成:
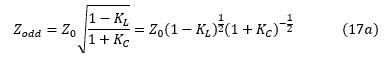
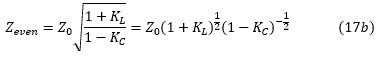
自'KL'和'KC'小于1,并且对于大多数实际案例将明显小于1,我们只能保留一阶项,以便:
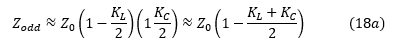
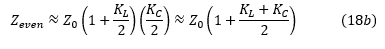
如果我们将方程(18a)与(8a)和(18b)与(10a)进行比较,很容易得出结论:
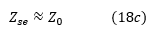
并且:
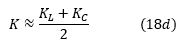
值得一提的是,在大多数带状线差分对的实际情况中,归纳如果信号层上方和下方的PCB材料的介电常数几乎相等,则耦合系数'KL'和电容耦合系数'KC'几乎相等。
两个串扰相关参数
在这里,我们还要定义另外两个参数,NEXT和FEXT:
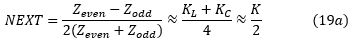
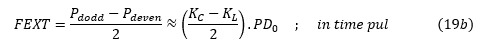
NEXT被称为最近的串扰系数。 FEXT称为远端串扰系数。这些参数在串扰分析中是重要的,当两条附近的线路中,一条是主信号线而另一条线是安静的线路,我们希望在该线路上确定由于主线路上的信号电压而引起的串扰电压。我们将在下一篇关于串扰分析的文章中详细阐述这一点。
-
传输线的特性阻抗分析2009-09-28 0
-
PCB传输线之SI反射问题的解决2018-09-21 0
-
PCB传输线原理2018-11-23 0
-
高速PCB布线差分对走线2018-11-27 0
-
什么是传输线?PCB的传输线结构是如何构成的?2021-06-29 0
-
PCB设计之实例解析传输线损耗2022-11-10 0
-
PCB传输线SI传输问题怎样解决2019-10-13 3149
-
PCB传输线中的差分对是怎样的2019-09-11 6876
-
PCB传输线原理_PCB传输线参数2020-03-12 3609
-
PCB板上多长的走线才是传输线?2020-11-06 5940
-
差分信号的传输与种类介绍2023-04-13 4980
-
什么是传输线?为什么传输线要测试差分讯号?2023-09-25 1392
-
传输线的类型有哪些?PCB上什么样的线才是传输线?2023-09-28 3707
-
什么是传输线?什么是信号完整性分析?为什么传输线要测试差分信号?2023-10-23 766
-
高速差分讯号传输理论2024-08-08 725
全部0条评论

快来发表一下你的评论吧 !

