

关于RNN和LSTM基础知识了解
人工智能
描述
一、RNN
递归神经网络(RNN)被提出用来处理80年代的输入序列时间信息。1993年,神经历史压缩器系统解决了“非常深度学习”任务,该任务需要及时展开RNN中的1000多个后续层。如图1所示,在传统的建模活动(例如前馈神经网络)中,我们显然会看到固定输入大小到固定输出大小的固定网络。在前馈神经网络的包围下,我们得到图1.b以揭示RNN的可区分性。
RNN能将输入动态更改为包含多个输入向量,每时间段一个,并且每个向量可以有很多列。
对于图2所示的RNN网络,假设输入序列为{x1,x2,…xt},则隐藏层节点的相应时间向量为H={ h1,h2,…ht },并且输出节点分别对应于Y={ y1,y2…yt },其中xi ,hi,yi(i=1,2…t)是神经网络相应层大的节点向量。
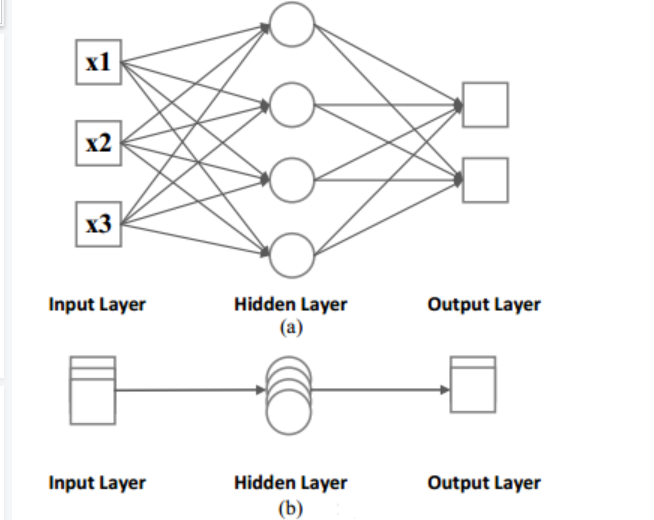
图1 前馈神经网络
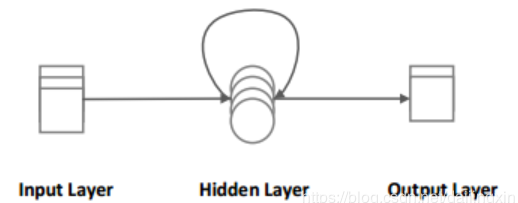
图2 递归神经网络(RNN)
在普通的前馈神经网络中,前向传播公式如下:

在前馈神经网络的RNN中,前向传播公式如下:

其中Wxh制是输入层和隐藏才能够之间的权重矩阵,bh是隐藏层的偏差矢量。Why是隐藏层和输出层之间的权重矩阵,by是输出层的偏差矢量。Whh图是隐藏层上一时刻与下一时刻之间的权重矩阵。σ是sigmoid()的激活功能。
由于RNN迭代复用隐藏层,导致RNN可以有效的保留序列的时间信息。如图1所示,一般的神经网络结构是从输入层到隐藏层再到输出层,并且每次的输出都与之前和之后的输入无关。如图2所示,RNN将在隐藏层中循环多路复用,因此它可以有效的保存序列的时间信息,并且每次输出的结果都受到所有先前输入的影响。
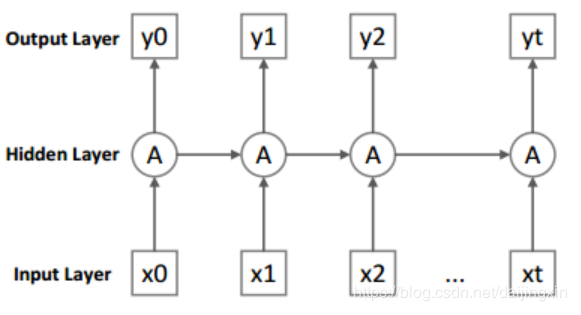
图3递归神经网络的发展
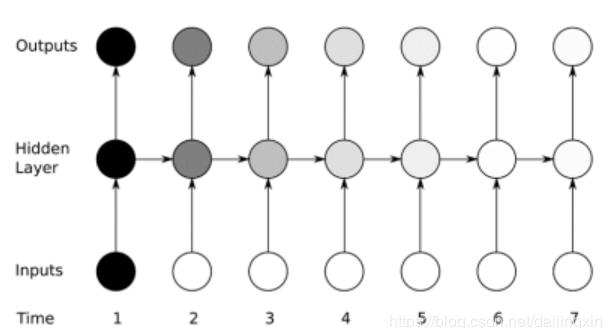
图4 消失梯度问题
在图3中,扩展了RNN的结构以解释RNN的隐藏层复用。除第一层外,RNN还将前一次隐藏层的结果与最新的输入一起用作当前时间的输入,从而影响后续的结果,同时是达到了保存序列时间信息的目的。
但是众所周知,RNN存在“消失梯度问题”。如图4所示,当梯度变得太大或者太小并且难以对输入数据集的结构中的长期依赖关系(10个时间步或更多)进行建模是就会出现这个问题。
二、 LSTM
为了克服RNN的“消失梯度问题”,Hochreiter和Schmidhuber于1997年提出了具有RNN架构的长短期记忆(LSTM)网络。
如图5所示,LSTM和其它神经网络模型之间的区别在于其独特的LSTM单元。当它与LSTM结合使用时,在不同时间阶段传播的LSTM的ht参数传输内部存储器状态Ct。尽管LSTM单元有很多改进的结构,但是它们都没有将模型的预测准确性进一步提升。 在图5中,从左到右的四个部分是忘记门,输入门,单元门和输出门。
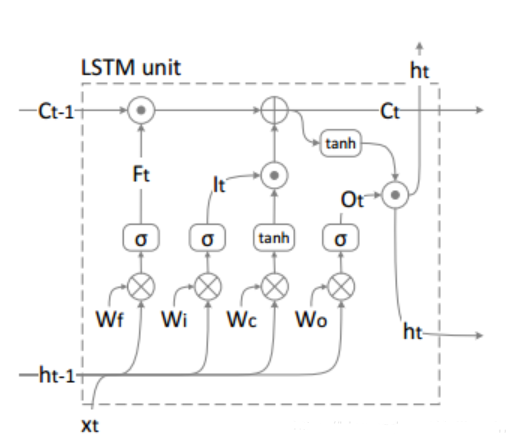
图5 长短期记忆网络单元
每个门对应的输入时ht-1,xt和它们对应的权重矩阵。 忘记门负责选择性地忘记存储在原始单元中的先前状态,以避免“消失梯度问题”。 输入门和单元门的结果相乘并加到先前的单元Ct-1上。最后,为了计算当前的输出ht ,我们使用了当前的单元门结果与出出门结果。使用到的相关公式如下:
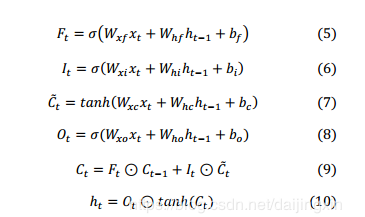
Ft、It、Ct和Ot分别是四个门各自的输出结果。W是从相应的输入到对应的门。例如,Wxy是相应的输入层到斜门的权重,并且Whi从上一刻就隐藏了起来。从层到输入门的权重bf,bi,bc和bo是四个门的偏置矢量,⊙是两个矢量或矩阵点乘法。σ和tanh()是常用的激活函数。
-
嵌入式系统基础知识2016-03-03 702
-
FPGA也能做RNN2018-07-31 0
-
介绍关于编程的基础知识2021-07-27 0
-
红外基础知识2011-11-02 909
-
放弃 RNN 和 LSTM 吧,它们真的不好用2018-04-25 20603
-
RNN及其变体LSTM和GRU2018-06-30 16505
-
循环神经网络(RNN)和(LSTM)初学者指南2019-02-05 959
-
一种具有强记忆力的 E3D-LSTM网络,强化了LSTM的长时记忆能力2019-09-01 11053
-
循环神经网络LSTM为何如此有效?2021-03-19 2873
-
RNN以及LSTM2022-03-15 1898
-
关于mos管的基础知识2023-01-29 4498
-
关于MOS管的基础知识2023-05-23 1547
-
如何理解RNN与LSTM神经网络2024-07-09 668
-
LSTM神经网络与传统RNN的区别2024-11-13 393
-
RNN与LSTM模型的比较分析2024-11-15 630
全部0条评论

快来发表一下你的评论吧 !

