删除二叉搜索树中的节点

今天分享的题目来源于 LeetCode 第 450 号问题：删除二叉搜索树中的节点。虽然它的难度是中等，但实际上很好理解，请往下看！

题目描述

给定一个二叉搜索树的根节点root和一个值key，删除二叉搜索树中的key对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；

如果找到了，删除它。

说明：要求算法时间复杂度为 O(h)，h 为树的高度。

示例:

root = [5,3,6,2,4,null,7] key = 3     5    /    3   6  /     2   4   7 给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。     5    /    4   6  /      2       7 另一个正确答案是 [5,2,6,null,4,null,7]。     5    /    2   6            4   7

题目解析

在二叉搜索树上删除一个节点，这道题目有一个隐含的条件，就是树上节点的值不重复。

另外题目还要求时间复杂度需要保证 O(h) 这里的 h 表示的是二叉树的高度。

其实这个题目是分成两个步骤的，第一个是找到对应的节点，第二个是删除节点。

因为是二叉搜索树，对于树上每个节点来说，其右子树的节点都要大于其左子树的节点，那么要找对应节点，我们可以从根节点开始，一路比较，大的话就去右边找，小的话就去左边找，这样每次我们都往下，可以保证时间复杂度是 O(h)。

当我们找到了要删除的节点，在删除这一步就会有很多的细节，主要是因为我们需要调整余下的结构，以维持二叉搜索树的性质。

针对这个问题，我们可以分情况讨论：

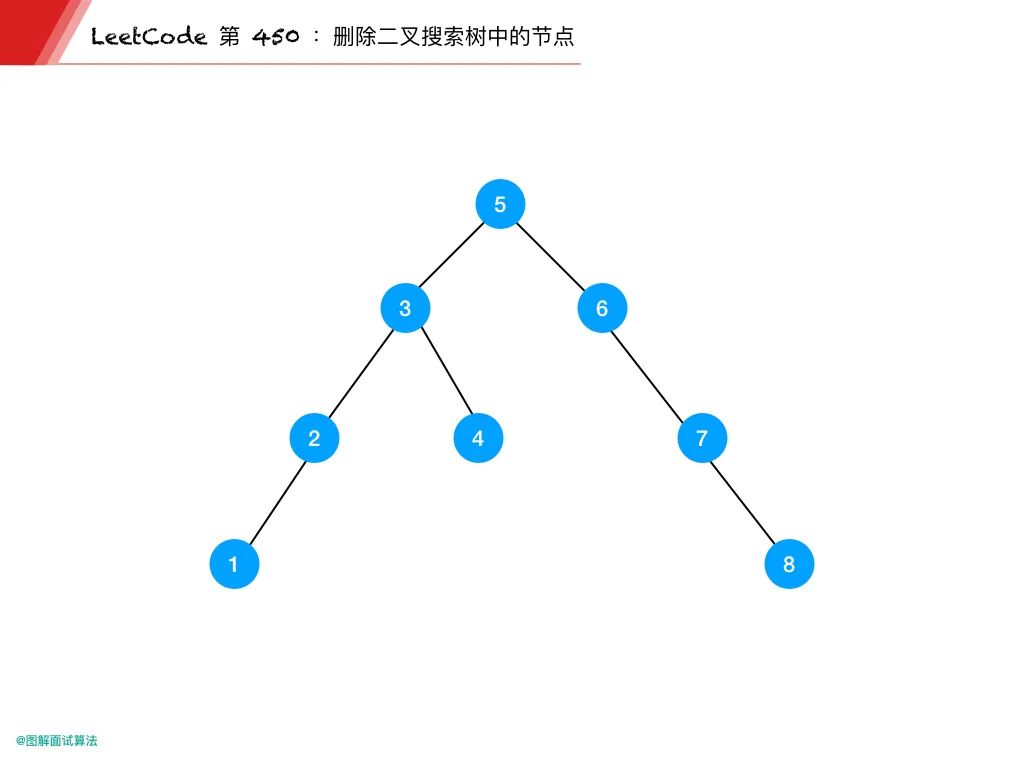
        5        /        3   6      /         2   4   7    /            1           8

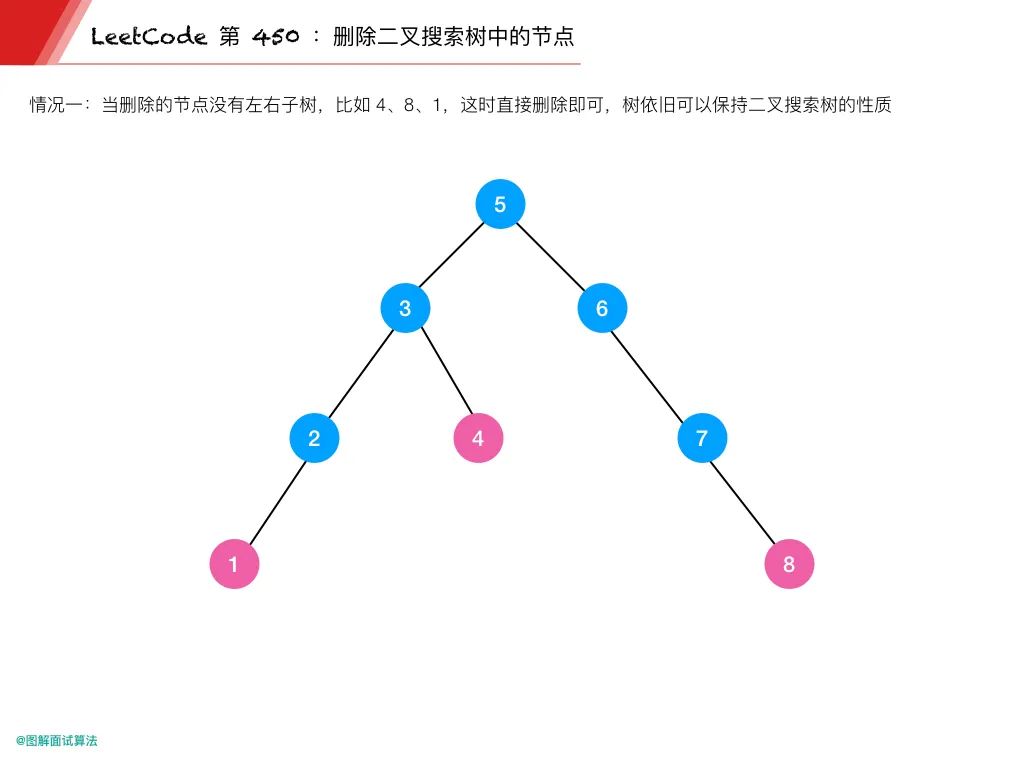
情况 1：当删除的节点没有左右子树，比如上图的 4、8、1
    这时直接删除即可，树依旧可以保持二叉搜索树的性质

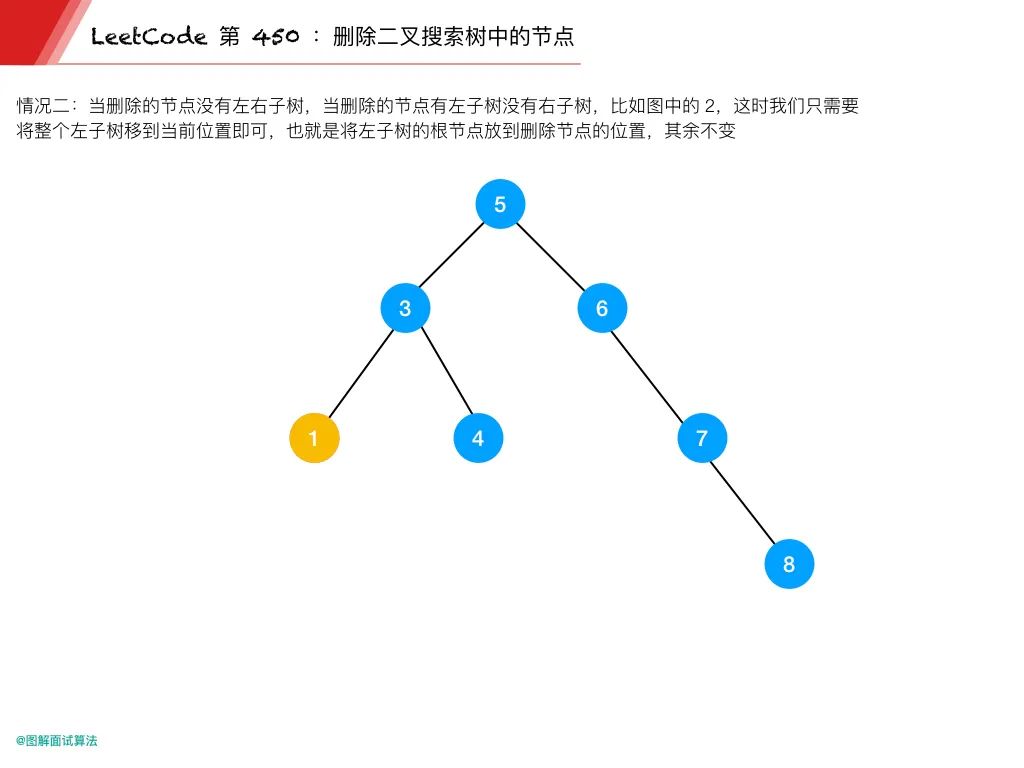
情况 2：当删除的节点有左子树没有右子树，比如上图的 2
    这时我们只需要将整个左子树移到当前位置即可
    也就是将左子树的根节点放到删除节点的位置，其余不变

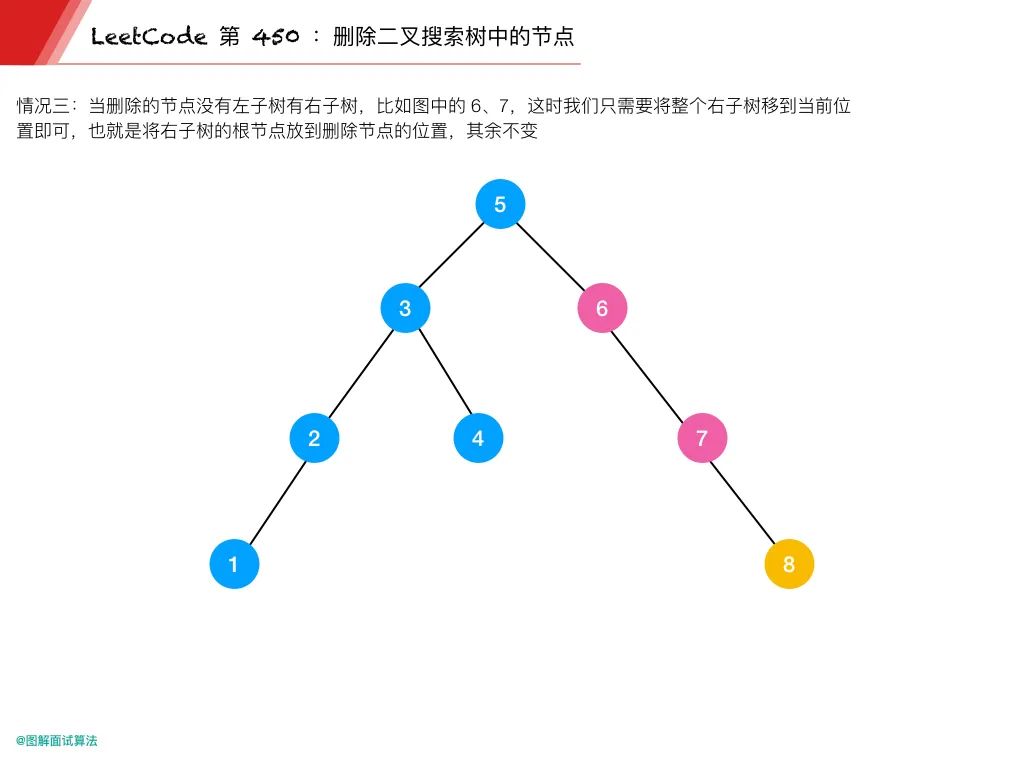
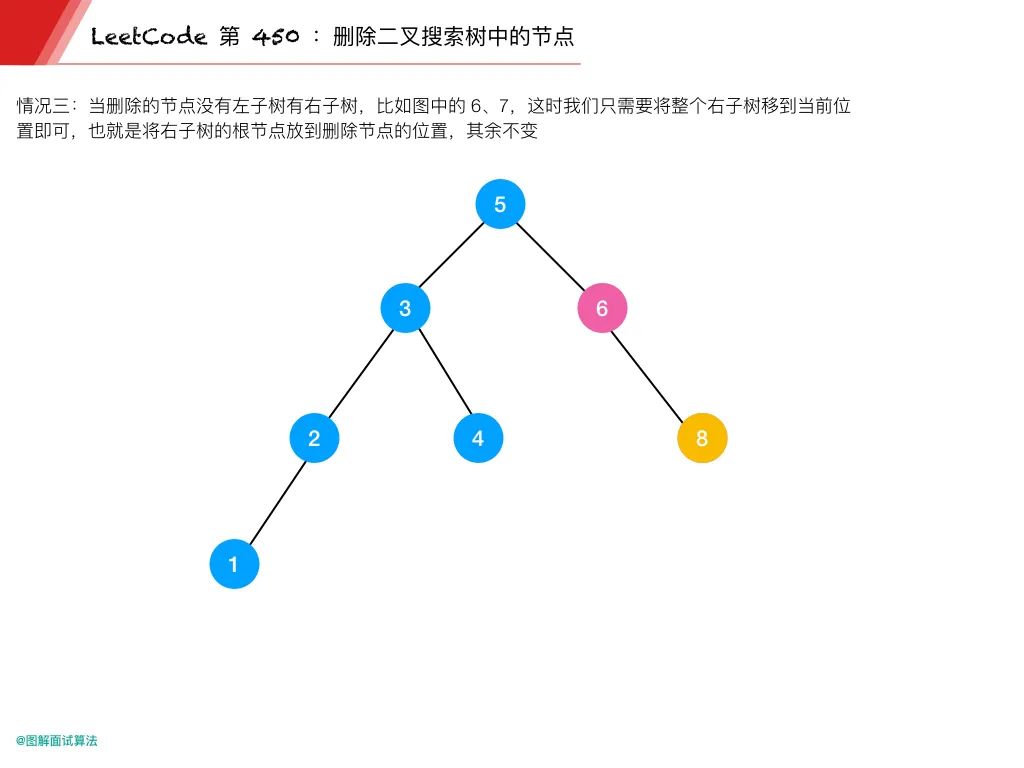
情况 3：当删除的节点没有左子树有右子树，比如上图的 6、7
    这时我们只需要将整个右子树移到当前位置即可
    也就是将右子树的根节点放到删除节点的位置，其余不变

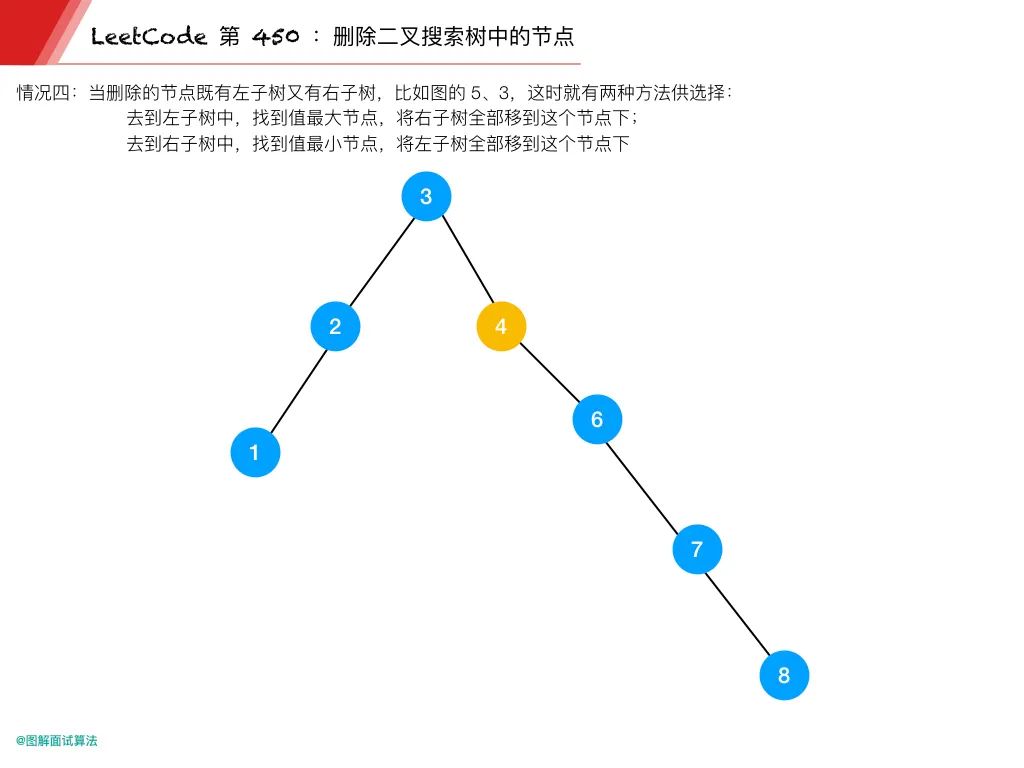
情况 4：当删除的节点既有左子树又有右子树，比如上图的 5、3
    这时就有两种方法供选择：
        去到左子树中，找到值最大节点，将右子树全部移到这个节点下
        去到右子树中，找到值最小节点，将左子树全部移到这个节点下

通过上面的讨论分析，我们有了大致的思路。在实现方面，我们可以借助递归来巧妙地达到删除对应节点的目的。

图片描述

参考代码

//五分钟学算法 public TreeNode deleteNode(TreeNode root, int key) {     if (root == null) {         return null;     }     // 当前遍历到的节点大于要找的节点，去左边继续找     if (root.val > key) {         root.left = deleteNode(root.left, key);     }     // 当前遍历到的节点小于要找的节点，去右边继续找     else if (root.val < key) {         root.right = deleteNode(root.right, key);     }      // 找到要删除的节点，进行删除操作     else {         // 情况 1 & 2         if (root.right == null) {             return root.left;         }          // 情况 3         if (root.left == null) {             return root.right;         }         // 去到删除节点的右子树，找到值最小的节点         TreeNode rightSmallest = root.right;         while (rightSmallest.left != null) {             rightSmallest = rightSmallest.left;         }         // 将删除节点的左子树全部移到这个节点下         rightSmallest.left = root.left;         // 返回右子树的根节点，放到当前删除节点的位置         return root.right;     }     return root; }