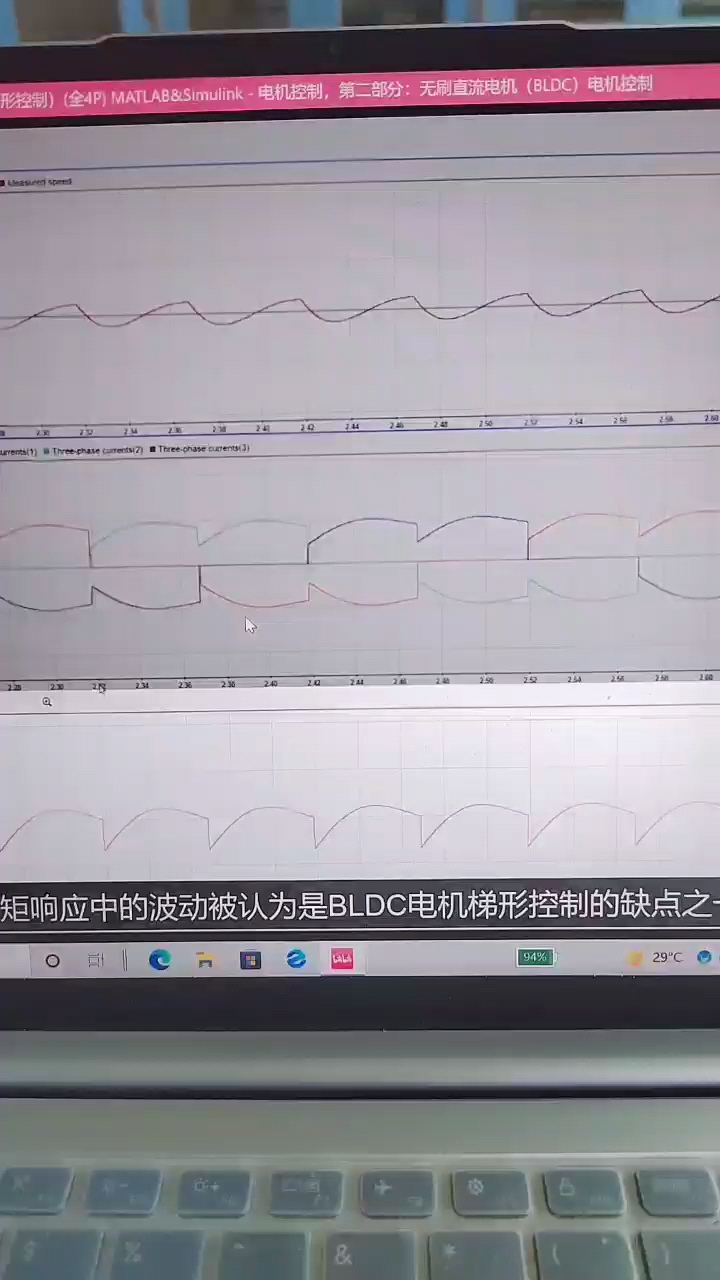
扬兴科技
企业
扬兴科技
企业


 森木磊石
企业
森木磊石
企业

 ICer消食片
ICer消食片
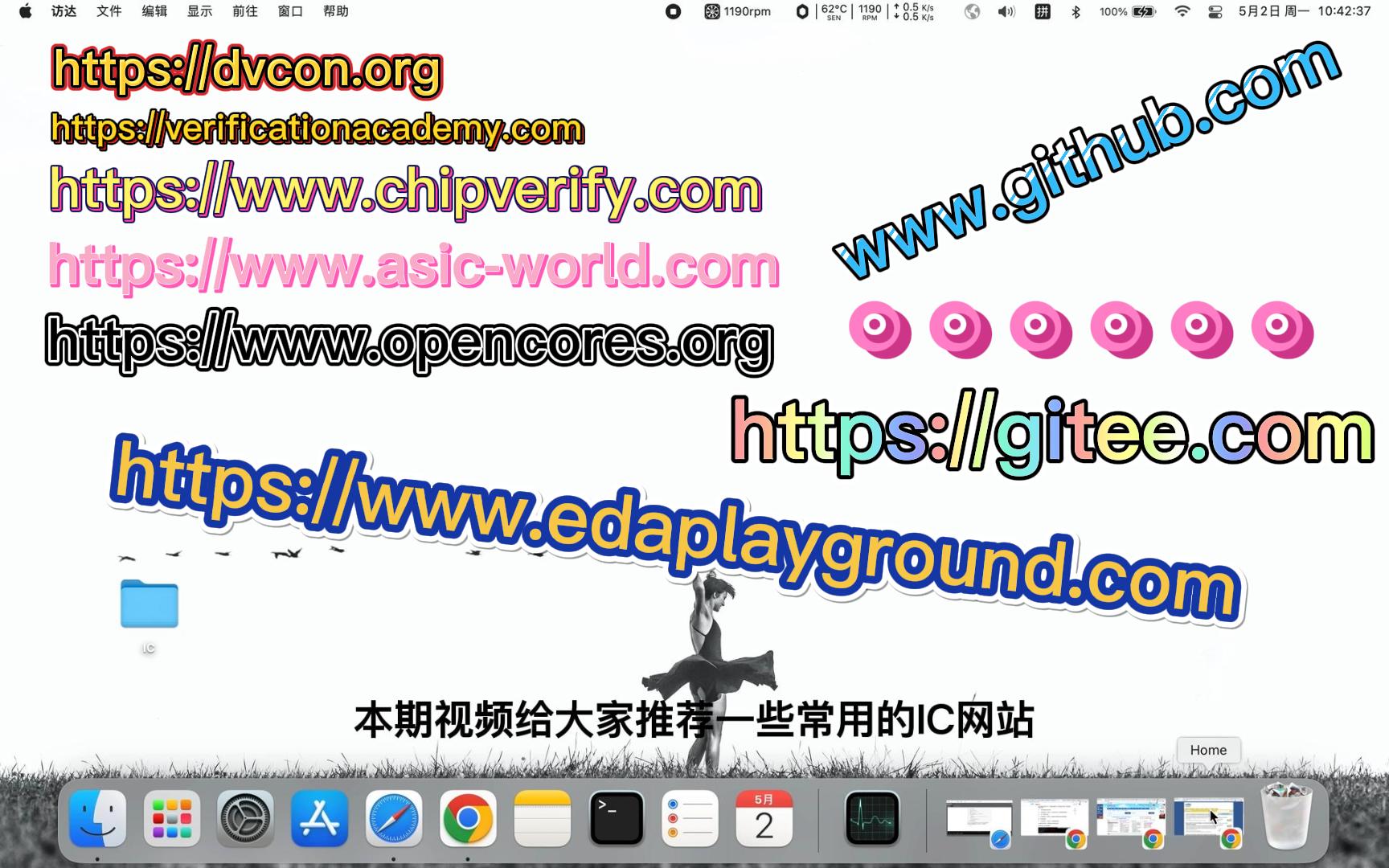

 工程师看海
专栏
工程师看海
专栏
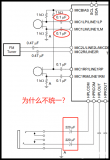
 Felix分析
专栏
Felix分析
专栏

 飞凌嵌入式
企业
飞凌嵌入式
企业

 花茶晶晶
专栏
花茶晶晶
专栏

 经纬恒润
企业
经纬恒润
企业

 亿佰特物联网应用专家
企业
亿佰特物联网应用专家
企业

 eeDesigner
专栏
eeDesigner
专栏

 Felix分析
专栏
Felix分析
专栏

 电子发烧友网官方
电子发烧友网官方


 电子发烧友网官方
电子发烧友网官方


 章鹰观察
专栏
章鹰观察
专栏

 Monika观察
专栏
Monika观察
专栏


 Simon观察
专栏
Simon观察
专栏

 Simon观察
专栏
Simon观察
专栏

 北汇信息POLELINK
企业
北汇信息POLELINK
企业

 jf_74264200
jf_74264200