

检测不到信号,是加点噪声,还是滤除噪声?
电子说
描述
在信号分析过程中,噪声常被认为是令人讨厌的东西,因为噪声的存在降低了信噪比,影响了有用信息的提取。然而在某些特定的非线性系统中,噪声的存在能够增强微弱信号的检测能力,这种现象被学者们称为 随机共振[1] 。
近期发表在Nature Communication上的一篇“ 硫化钼光电检测器中的随机共振[2] ”文章,作者 Akhil Dodda就在文章综述部分热情介绍了随机共振在很多领域中的现象。
比如一种体型硕大的白鲟依靠它的长长鼻子上的电感受器来探知水中的浮游生物水蚤发出的微弱电信号来进行捕食。这在河砂泛滥、浑浊昏暗的河道内对于白鲟的生存很重要。动物行为学家发现,水里增加的随机噪声会增加白鲟对水蚤感知的距离[3] 。当然如果噪声强度超过一定阈值白鲟自己也会晕头转向。同样得益于噪声共振的还有小龙虾 。
噪声共振在人类康复治疗中也得到应用,比如对 听觉治疗[4] 、 触觉感知 、 身体平衡控制 等方面。
为什么在传感器和信号处理应用中,随机共振(这个名词来自于别的领域)应用却很少呢?Akhil Dodda总结道:这是因为用于改善信号接收和处理的传统方式(锁相放大器、低噪音放大器等)现在占主导地位并还具有很大的潜力,所以人们常常忽略来自于其他领域的新的思想。
但是在万物互联(IoT)的现在数量巨大的物联设备对于传感器和通讯设备的低功耗和高灵敏度的需求日益提高,随机共振就给低功耗、弱信号检测提供了新的思路。
Akhil Dodda在论文中介绍了他们制作的基于二硫化钼(MoS~2~)制作的二维光电检测材料,与传统的传感器相比,它所需要的能量和空间非常小,可以在物联网应用中找到广泛的应用。
▲ 基于MoS2二维材料进行微弱蓝光信号检测
论文后半部分给出了使用随机共振方式如何提高了MoS~2~检测信号灵敏度及其指标。相比于基于硅材料的光电管,这种传感器功耗在检测同样光信号的情况下降低了四个数量级(2.8微焦 →470皮焦)。也许你对于材料和传感器不感兴趣,但是通过论文的前半部分的介绍,可以了解随机共振在工程中的具体应用。
下面的框图显示了随机共振帮助检测信号的系统组成:一个非线性阈值检测器件;一个被检测窄带(相关信号)弱信号,比如周期正弦号;一个随机信号源。
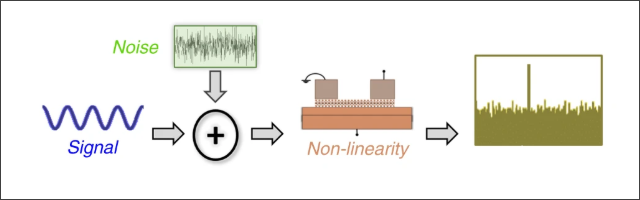
▲ 随机共振(Stochastic Resonance)信号检测示意图
在没有噪声的情况下,如果被检测信号幅值很小,低于传感器检测门限,系统无法感知信号的存在。
在传感器输入增加噪声之后,信号部分时刻的值就会突破检测器的阈值,检测器就输出相应的时间信号。再对输出信号进行频谱分析,就可以检测出弱信号对应的频率分量的存在。
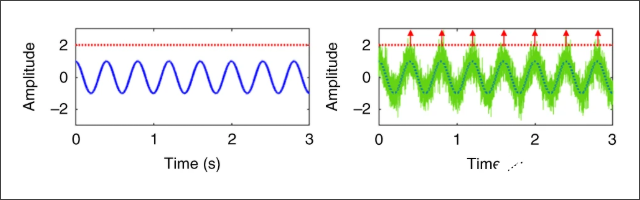
▲ 增加噪声后可以被检测处的正弦波分量
在 Stochastic resonance in MoS 2 photodetector | Nature Communications[2] 论文中,被检测的光信号是2.5Hz的方波信号(如下图信号b)。它所引起光传感器输出电流波形如下图的C,对应的信号频谱如下图的D。信号采样频谱为200Hz。
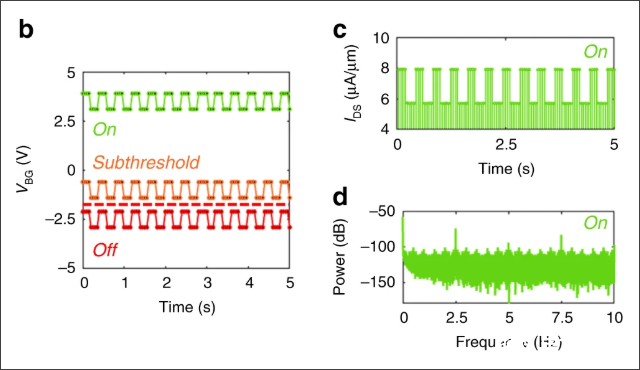
▲ 被检测信号是方波信号(b)
当信号的幅值超过传感器的阈值时,可以在采集到的数据中看到信号的波形以及对应的频谱(下图左)。如果信号很弱,幅值低于传感器的阈值。则采集到的电流则是随机的信号,频谱中也不包含方波周期信号的频谱(下图右)。
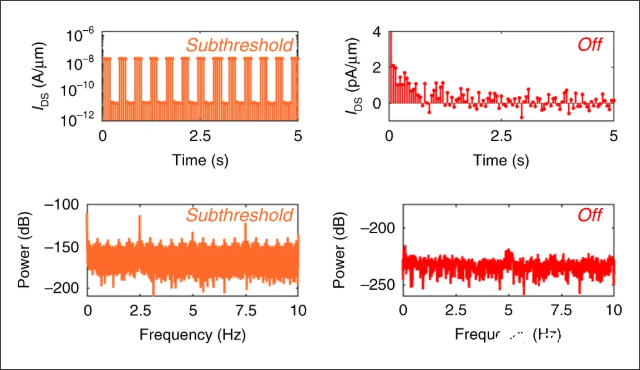
▲ 两种场效应传感器不同阈值下检测信号波形和频谱
为了说明噪声的作用,论文作者设置了光信号的幅值低于传感器的阈值,然后再逐步添加高斯白色噪声。随着高斯噪声的增加,就会在采集到的传感器输出信号中检测到方波信号的频谱。
当添加的噪声信号达到一定数值时,检测到的信号强度与噪声的比值(信噪比:SNR)会达到一个最大值。随后随着噪声的幅值增加,信噪比也会降低。
下面显示了不同噪声叠加下,型号的波形与检测信号频谱的波形。
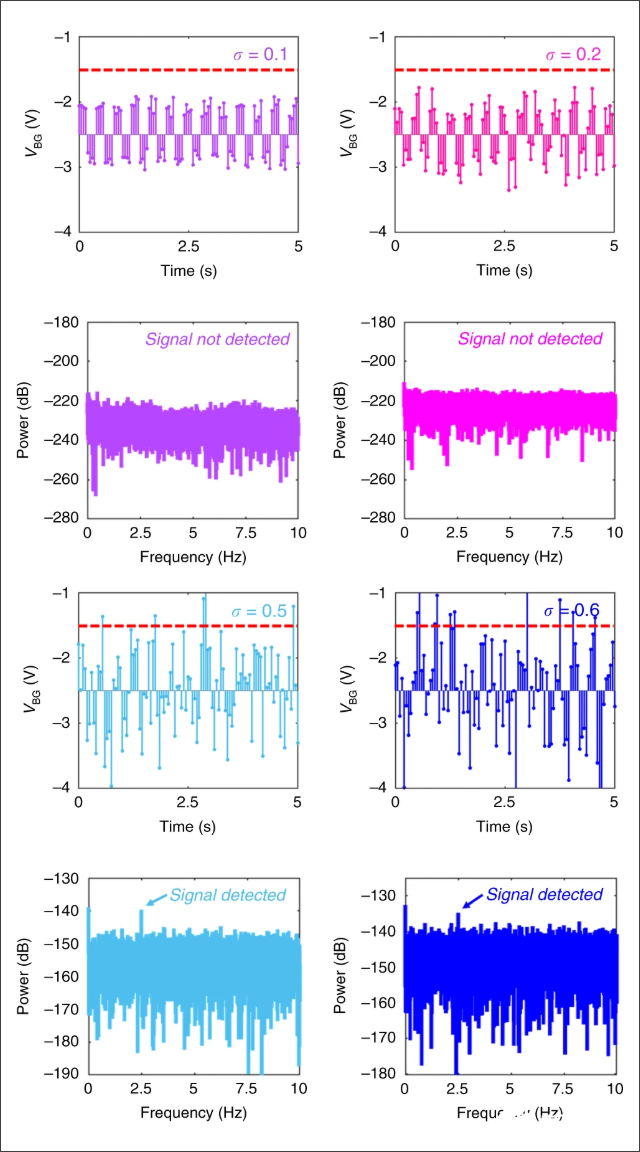
▲ 从上往下逐步增加噪声所对应的信号检测频谱
由于叠加的是白色噪声,所以随着采集信号的时间(数据量)的增加,信号检测的信噪比也会提高。论文就结合添加噪声强度和检测时间两个参数,通过仿真给出检测到的信噪比的分布。可以看到,提高检测的信号的质量,需要确定合适的添加噪声的强度,以及尽可能增加检测的时间。
▲ 噪声幅值采样时间对信号检测的影响
增加检测时间是传统的方式,但会增加检测所需要到能量。添加恰当的噪声来提高检测质量可以不用付出额外的能量代价。但问题来了:在实际应用中该如何确定合适的噪声添加量呢?
就像 精度不够,噪声来凑[5] 那样利用噪声来提高测量信号的精度,应用信号是缓变的低频信号(相当于窄带信号),与前面噪声共振论文中要求检测信号是一个周期(窄带、相关信号)信号一样,在统计意义上可以通过后期处理与噪声信号进行分离。并不是在所有情况下都可以应用噪声共振,它的两个必要条件是:
系统中存在非线性过程;
检测的信号具有很强的统计特性(缓变、窄带、或者其他可以进行稀疏采样的特性)
如果不满足,噪声共振就会变成噪声捣乱了。
作者:卓晴
来源:TsinghuaJoking
-
噪音监测模块噪声传感器 # 立杆噪声传感器# 噪音监测# 噪音报警仪# 噪声检测仪# 工业级噪音模块噪声模块pingao141378 2022-07-12
-
[14.1.1]--14.1.1学习视频:噪声参量未知时的信号检测jf_75936199 2023-03-09
-
引入输入滤波器来滤除噪声设计2018-07-05 0
-
如何滤除DC / DC设计中的噪声2018-07-24 0
-
ADC输入噪声面面观:噪声是利还是弊?2018-12-06 0
-
噪声主要在0hz到1000hz之间,有效信号也在0hz到1000hz之间,能否用软件算法提取有效信号而滤除噪声呢?2019-09-28 0
-
噪声调频信号检测方法2011-05-11 4261
-
精通信号处理设计小Tips(8):检测淹没在噪声中的信号2014-01-06 7476
-
从电容滤除噪声谈电容滤波半径2020-12-04 4734
-
使用MATLAB实现LS滤波器滤除ECG信号噪声的实验说明2020-11-13 1426
-
如何将高频噪声从信号中滤除掉?2022-12-09 3532
-
信号放大器还是噪声放大器?2023-02-28 1030
-
噪声是高频信号还是低频信号?2023-09-19 4036
-
相位噪声定义 相位噪声来源 相位噪声对信号的影响2024-01-29 1049
全部0条评论

快来发表一下你的评论吧 !

