

排序算法里面的另外一种排序算法:归并排序!
电子说
描述
今天继续给大家分享排序算法里面的另外一种排序算法:归并排序!
一、归并排序:
1、归并排序操作的核心思想:
a、确定分界点:mid=(l+r)/2
b、递归排序左边和右边(排完左右两边的数,就会成为两个有序的序列了)
c、归并(把上面的两个有序序列合并成一个有序的序列,用一个简单的词来说,就是合二为一!)
2、举例:
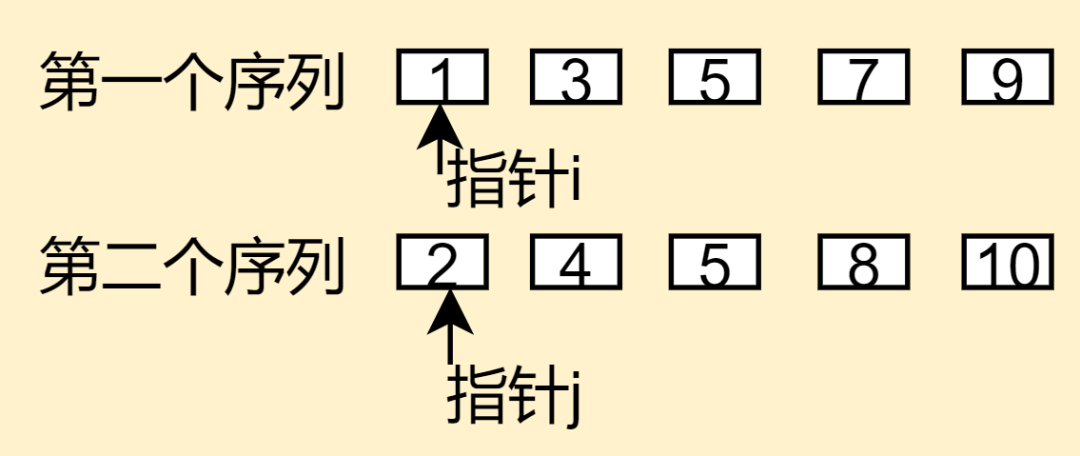
比如上图我们有两组已经排好的序列数字,我们要进行第三步合并,该如何进行呢?思路如下:
a、这里先定义一个空的数组res,它主要是为了临时存放合并序列排序好的数字;我们从图中可以看到,第一个序列指针i指向数字1,第二序列指针j指向2,这个时候我们要比较两个数字的大小,小的数字就放到临时数组res里面去,这里我们明显知道数字1小于2,所以把1放到临时数组res里去
b、然后指针i往下移动,如下图所示,再次进行比较,明显发现指针j指向的数字2更小,把它放到res里面去,然后指针j往下移动,指针i不动,后面依次类推
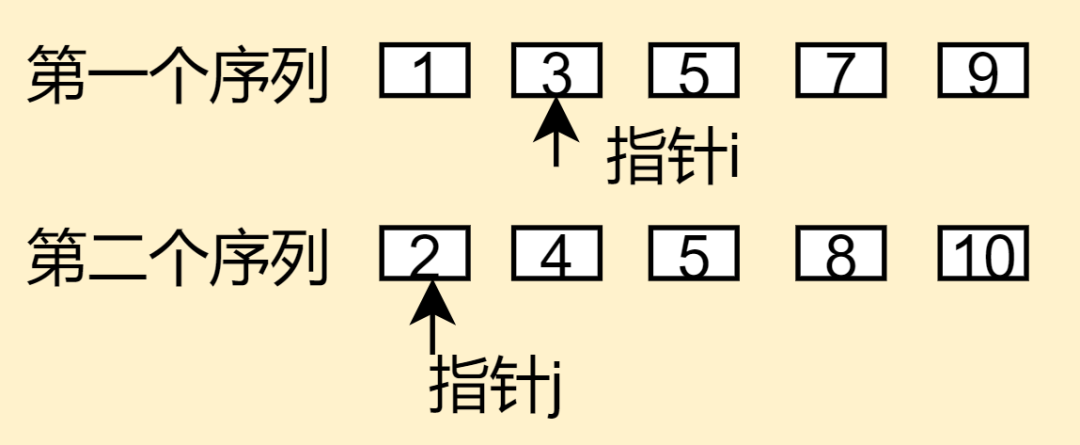
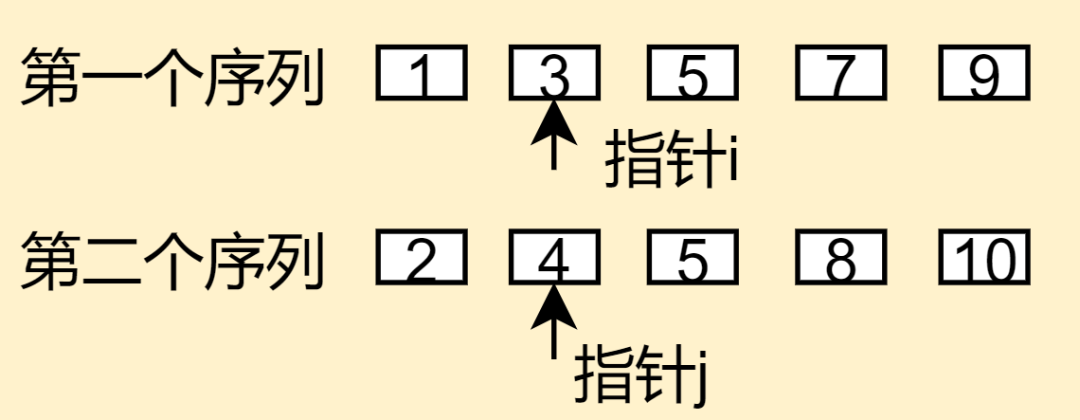
c、如下图所示,两个指针都指向了数字5,如果遇到两个数字一样的话,一般是把第一个序列的数字放到临时数组res里面去,这点稍微要注意一下
d、最后把临时数组里面的是数字放到原来的数组里面去
注意:一个算法稳定,并不能说它的时间效率是稳定的;这里的稳定是说两个序列中有两个数是相同的,如果在排完序之后,他们的位置还是没有发生变化的话,那么这个排序就是稳定的,反之亦然!
3、归并排序的平均时间复杂度的计算推导:
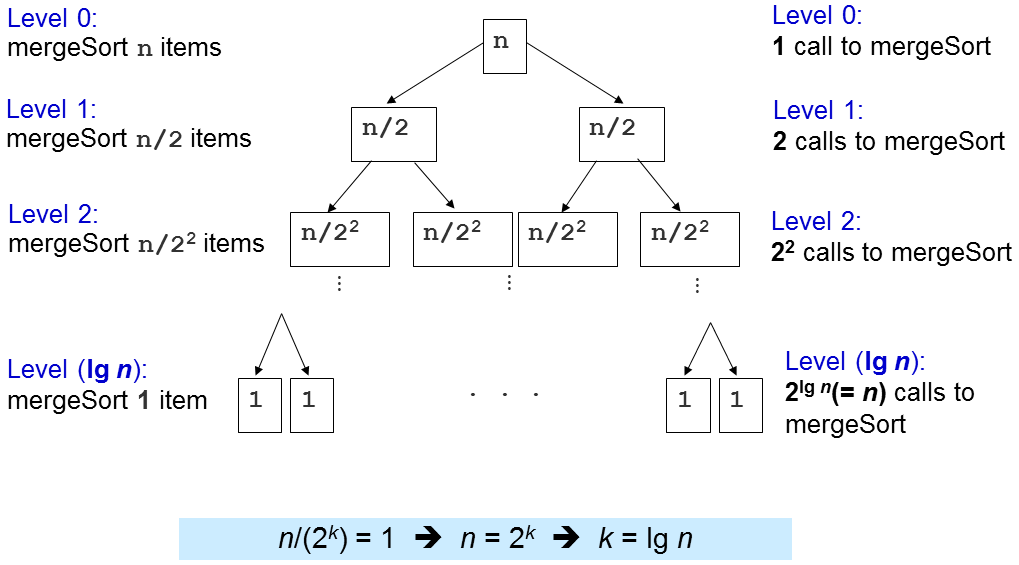
注:图片来源:https://visualgo.net/zh/sorting
从图片的纵性来分析,当拆解到1的时候,这个时候什么数等于n除于它等于1,通过计算,我们知道是logn,然后再从横向分析,我们要最多比较n个数字,所以归并排序的时间复杂度就是:nlogn
二、代码示例:
代码:
#include
结果:
责任编辑:lq
-
嵌入式stm32实用的排序算法 - 交换排序2018-04-12 0
-
各种排序算法的时间空间复杂度、稳定性2021-12-21 0
-
介绍几种常用的排序算法C实现2021-12-21 0
-
C语言教程之归并排序2016-04-22 377
-
C语言教程之几种排序算法2017-11-16 1763
-
常用排序算法分析2018-07-13 2172
-
实用的排序算法 - 交换排序2020-03-20 1757
-
排序算法分享:归并排序说明2020-12-24 783
-
如何去实现并验证一种归并排序?2021-06-23 1535
-
解析数据结构的常用七大排序算法2022-03-16 1708
-
随机数字排序教程2023-03-24 1016
-
FPGA排序-冒泡排序介绍2023-07-17 1120
-
排序算法有哪些2023-10-11 630
-
十大排序算法总结2023-12-20 1143
-
用FPGA实现双调排序的方法(2)2024-03-21 656
全部0条评论

快来发表一下你的评论吧 !

