

卷积神经网络是怎样实现不变性特征提取的?
描述
图像特征
传统的图像特征提取(特征工程)主要是基于各种先验模型,通过提取图像关键点、生成描述子特征数据、进行数据匹配或者机器学习方法对特征数据二分类/多分类实现图像的对象检测与识别。卷积神经网络通过计算机自动提取特征(表示工程)实现图像特征的提取与抽象,通过MLP实现数据的回归与分类。二者提取的特征数据都具不变性特征。

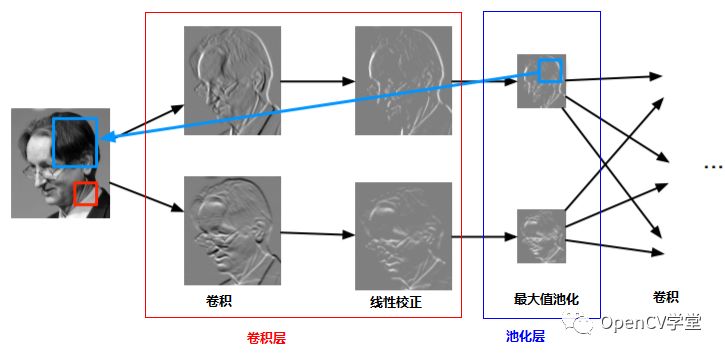
卷积神经网络为什么能提取到图像特征,其关键在于卷积神经网络有两种不同类型的层
-卷积层(convolution layers/detection layers)
-池化层(pooling layers)
卷积层
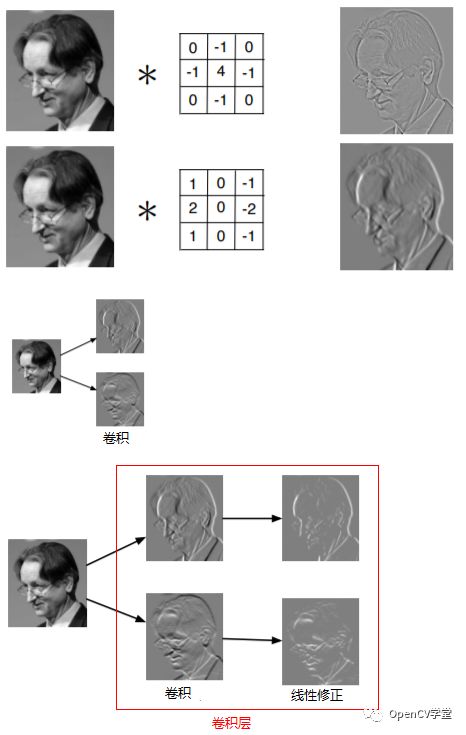
卷积层是一系列滤波器集合(filters set)、它的输出结果被称为特征映射(feature maps),每个feature map都一个filter在图像上卷积得到的输出。一般情况下都会输出结果加线性修正,对卷积层常用就是ReLU

这样做的好处是:
卷积是一个线性操作,我们需要一个非线性组合,否则两个卷积卷积层还不如一个卷积层
两个相反方向的边缘不应该被取消
使图像梯度值更加的稀疏、有助于提高反向传播的效果
假设灰度输入图像,有两个filter,卷积层生成过程如下所示:
假设灰度输入图像,有两个filter,卷积层生成过程如下所示:
膨胀卷积
通常我们常见的卷积层操作使用的filter都是基于连续邻近像素的,除了这种卷积filter之后另外还有一张卷积filter被称为膨胀卷积,其算子的分布更加的稀疏,图示如下:
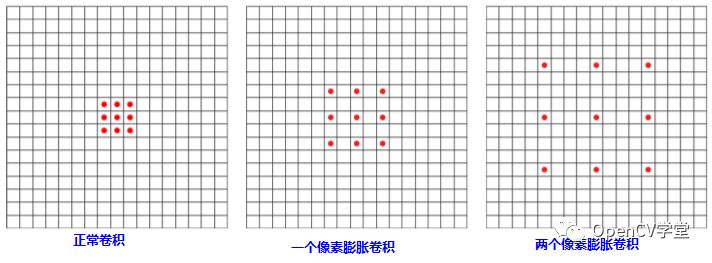
膨胀卷积在不增加网络总参数的情况下,提升每个感受野的尺度大小。
1x1卷积
1x1的卷积首次使用是在Network In Network网络模型中,后来受到越来越多的关注,在一般情况下我们的卷积是2D的,1x1的卷积操作是毫无意义的,但是对卷积神经网络来说,它的卷积层是三维的,所以1x1的卷积操作是有意义的。
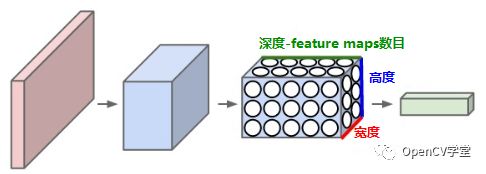
卷积层大小计算
对于一个输入大小WxW的feature map,假设Filter的大小位FxF,卷积时填充边缘P个像素、卷积步长(stride)为S则输出的大小为:
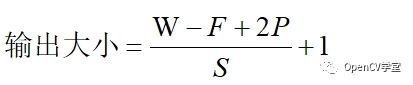
在多数深度学习框架中支持两种输出大小计算:
padding = “same”
意味着使用填充边缘的方式,输出大小与输入的feature map大小保持不变
padding = “valid”
意味着不使用边缘填充,即P=0此时输出大小为:
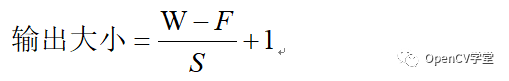
池化层
在卷积层提取到的特征数据不具备空间不变性(尺度与迁移不变性特征),只有通过了池化层之后才会具备空间不变性特征。池化层是针对每个feature map进行池化操作,池化操作的窗口大小可以指定为任意尺寸,主要有两种类型的池化操作
-下采样池化(均值池化)
-最大值池化
下采样池化
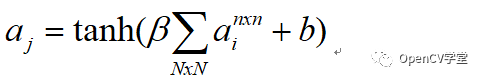
对每个窗口大小取均值,然后乘以标量beta加上我们增益偏置b的输出
最大值池化
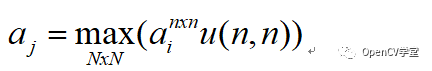
无论是选择哪种池化方式都会输出一个新低分辨率feature map,多数时候这个过程中会包含一定的信息损失,所以卷积神经网络一般通过扩展深度(增加feature map的数量)来补偿。
重叠窗口与稀疏窗口
在进行池化的时候我们如果选择步长=1进行池化,通过这样的池化方式输出的结果我们称为重叠池化输出,它不利于特征的稀疏生成,重叠窗口池化与均值池化都有这样的缺点,所以经常采样的是最大值池化,同时不会进行窗口重叠,有实验结果表明,在卷积层保持相同feature map与参数的情况下,最大值池化的结果明显优于重叠池化与均值池化,而且网络的深度越深,两者之间的准确度差异越大。
总结
最终卷积神经网络经过池化层操作对单位像素迁移和亮度影响进行了校正,做到了图像的迁移与亮度不变性的特征提取、而且在池化过程中通过不断的降低图像分辨率,构建了图像的多尺度特征,所以还具备尺度空间不变性,完成了图像不变性特征提取工作。
编辑:jq
-
如何将脉冲耦合神经网络,体视学等结合实现药材显微图像的特征提取?2015-04-16 0
-
可分离卷积神经网络在 Cortex-M 处理器上实现关键词识别2021-07-26 0
-
卷积神经网络模型发展及应用2022-08-02 0
-
基于三通道全连接层的卷积神经网络特征提取2017-11-28 1462
-
基于卷积循环神经网络的自动代码特征提取模型2021-03-30 677
-
为什么卷积神经网络可以做到不变性特征提取?2021-05-20 5260
-
卷积神经网络的基本原理 卷积神经网络发展 卷积神经网络三大特点2023-08-21 2425
-
卷积神经网络层级结构 卷积神经网络的卷积层讲解2023-08-21 7601
-
卷积神经网络算法代码matlab2023-08-21 1209
-
cnn卷积神经网络简介 cnn卷积神经网络代码2023-08-21 2678
-
基于卷积神经网络的双重特征提取方法2023-10-16 604
-
卷积神经网络的基本结构及其功能2024-07-02 1590
-
卷积神经网络的原理与实现2024-07-02 569
-
卷积神经网络的实现原理2024-07-03 544
-
卷积神经网络的基本概念、原理及特点2024-07-11 1041
全部0条评论

快来发表一下你的评论吧 !

