MATLAB中的振动分析与信号处理分析

模态分析主要研究频率域内系统动态特性。

通过模态分析方法搞清楚了结构物在某一易受影响的频率范围内的各阶主要模态的特性，就可以预言结构在此频段内在外部或内部各种振源作用下产生的实际振动响应。

模态分析主要分为解析模态分析和试验模态分析

解析模态分析

通常我们针对一个线性定常系统进行动力学描述可以得到方程组：

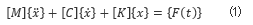
其中，[M] 是质量矩阵，[C] 是阻尼矩阵，[K] 是刚度矩阵，{x(t)} 是位移向量, {F(t)} 是力矩阵。 我们的目标是求解这个线性定常系统振动微分方程组得到 {x(t)}，也就是系统上各点随时间的位移。 对于单自由度的系统是方便求解的，所以对于这种多自由度系统我们首先想到的是通过坐标变换，用一组新的正交基（模态空间里的基）去描述 {x(t)}，例如 [P⁻¹]x(t)，来实现对方程组 (1) 解耦，从而将问题转化为互相独立的子方程（组），用更少自由度甚至单自由度的方程进行求解。 其中 [P⁻¹] 就是模态矩阵，其每列为模态振型，它描述的是在新的解耦后的坐标系中的各维坐标与原来坐标系中各个维度的线性关系。

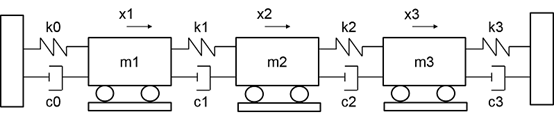
例如对于一个简化的多自由度的弹簧系统，这个线性定常系统由 3 个相同重量的模块组成，m₁=m₂=m₃=m，他们中间用弹簧链接, 为了简化问题，我们设弹簧的劲度系数 k₀=k₁=k₂=k₃=k，阻尼系数 c₀=c₁=c₂=c₃=0。 定义 x₁, x₂, x₃ ‍为每个质量块的位移，另外 k₀ , k₄ 边缘两端的位移。由于两端固定，都为 0。每个质量块的运动方程分别为：

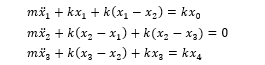
将上述方程写为矩阵形式，上述运动学方程组可以简化为：

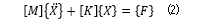
其中

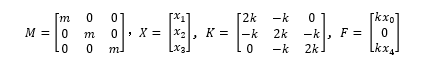
对于方程组 (2)，如何进行坐标解耦呢？ 计算时运动学方程组 (2) 右侧项可以忽略, 只保留质量矩阵项 [M] 和刚度矩阵 [K] 项，即

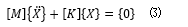
对于方程组 (3) 通常的做法是转换为：

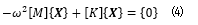
本质对方程组 (4) 解耦实际上就是求解质量矩阵关于刚度矩阵的广义特征值的问题。也就是计算得到特征值，

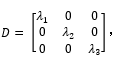
和特征向量，

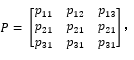
使得 [M][P]=[K][P][D]  (5) 其中特征向量 [P] 即为模态向量（空间基向量），为对应的特征值对角阵对应解耦后固有频率的平方，即

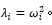
具体此处不做推导，但可以简单的从必要性上进行解释： 假设已经通过空间变换矩阵得到新的坐标

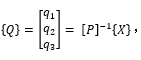
我们计算一下特征向量矩阵是否将原始方程组坐标由 {X} 变换为后 {Q} 得到单自由度的二阶常微分方程组。 我们将 {X} =[P]{Q}  带入方程 (3) 得到

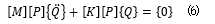
同时我们将 (5) 带入 (6) 可以得到

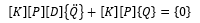
在 [K][P] 均可逆的条件下，我们得到方程

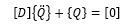
即：

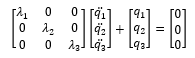
也就是完全解耦的单自由度的二阶常微分方程，接下来可以单独求解 q₁(t), q₂(t), q₃(t), 最后只需要再做一次 [P] 变换将模态空间坐标变换到物理坐标即可。

‍‍‍‍‍‍‍‍‍

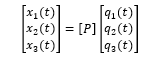
% 'M' 是质量矩阵,'K' 是刚度矩阵. 'm' 质量块质量,单位 Kgs

% 'k' 刚度系数,单位N/m. 'P' 和'D' 是特征向量和特征值.

m = 0.003;

k = 180000;

M = m*eye(3);

K = k*[2 -1 0 ;

-1 2 -1 ;

0 -1 2  ];

% P为特征向量：变换矩阵，D为特征值：固有频率的平方，w_nat 包含自然响应频率.

[P,D] = eig(K,M)

w_nat = sqrt(D)

% 我们查看低阶模态振型，也就是低频振型，可以尝试设置number

% 查看三阶模态振型'EIGS' 函数可以用来计算特征值和特征向量

number = 3;

[P,D]=eigs(K,M,number,'smallestabs');

% 因为系统两端固定，模态振型坐标在这两端为0

vect_aug1 = [0 0 0;P;0 0 0];

c = ['m','b','r'];

figure(1)

for i=1:size(vect_aug1,2)

plot(vect_aug1(:,i),c(i))

hold on;

end

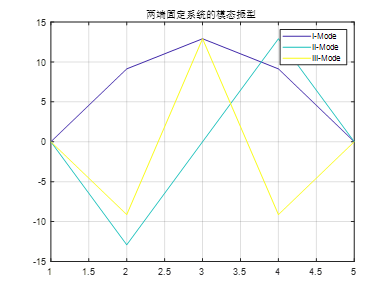
最终

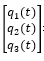
和

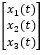
的求解以及绘制都可以用通过 MATLAB 脚本实现。大家可以自己尝试。 当然对于我们的系统不可能是这种简单的系统，通常要结合有限元的手段进行计算。 MATLAB 中的 Partial Differential EquationToolbox 对于满足我们一些基础的需求可以提供求解方案。 我们看一个基于 MATLAB 有限元计算模态的示例。 本示例是对 KinovaGen3 机械臂肩部关节部件进行模态和频率响应分析。机械臂通过多个关节链接，一端固定。这些链接结构强度要够大以避免电机带动负载运动时产生振动。 机械臂终端的负载会让每个链接处产生压力。压力的方向取决于负载的方向。此示例主要展示如何分析 Kinova Gen3 超轻量级机械臂的肩部关节连接部件在一定压力下可能的形变。

模态分析MATLAB 中有限元求解流程

model = createpde('structural','modal-solid');

importGeometry(model,'Gen3Shoulder.stl');

generateMesh(model);

structuralProperties(model,'YoungsModulus',E, ...

'PoissonsRatio',nu, ...

'MassDensity',rho);

将 facelabel 可视化出来方便设置边界约束和负载。

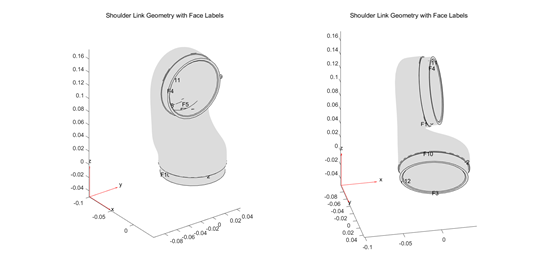
face3 是固定的，face4 是活动的。设置约束

structuralBC(model,'Face',3,'Constraint','fixed');

在关心的频率范围进行模型求解。

RF = solve(model,'FrequencyRange',[-1,10000]*2*pi);

modeID = 1:numel(RF.NaturalFrequencies);

通过对结果除以2pi,得到Hz单位的频率值：

tmodalResults = table(modeID.',RF.NaturalFrequencies/2/pi);

tmodalResults.Properties.VariableNames = {'Mode','Frequency'};

disp(tmodalResults);

同样我们需要可视化模态振型。最好的方式是以各阶模态频率的简谐振动动画显示出来，此处显示前六阶模态振型：

频率响应分析模拟机械臂关节在压力载荷下的动力学，假设附加其上的连杆对各半面分别施加大小相等方向相反的压力。分析面上某点的频率响应和形变。

同样跟上述流程一样，创建结构，导入几何形状，生成网格。

其他过程跟模态分析相同，区别在于加一个力，使用 pressFcnFR 函数在面 4 上施加边界载荷。 这个函数作用一个推力和一个扭转压力信号。推压分量是均匀的。扭力对左侧面施加正压力，对右侧施加负压力。

structuralBoundaryLoad(fmodel,'Face',4,'Pressure',@(region,state)pressFcnFR(region, state),'Vectorized','on');

这个压力函数跟频率无关，作用于所有频率。

同样进行求解

R = solve(fmodel,flist,'ModalResults',RF)

我们可以看面 4 对应的负向负荷最大的点（0.003; 0.0436; 0.1307）对应的位移

queryPoint = [0.003; 0.0436; 0.1307];

queryPointDisp =R.interpolateDisplacement(queryPoint);

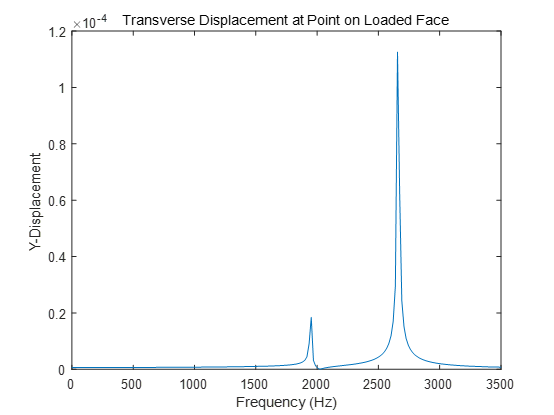
响应的峰值出现在 2662Hz 附近，与二阶模态接近。在接近 1947Hz 的一阶模态上也会出现小的响应。

通过使用 max 函数找到峰值响应频率对应的峰值和索引。

[M, I] = max(abs(queryPointDisp.uy))

M = 1.1256e-04

I = 152 绘制峰值响应频率处的变形。

可以看到所施加的载荷主要激发了部件的开口模态和弯曲模态。 通过上面两个示例，我们针对计算模态的场景可以在 MATLAB 中通过相应的内置函数做探索研究。  

试验模态分析

试验模态分析主要是通过实测实验数据进行频率响应估计并计算相应模态参数的一种方法。

我们通过 MATLAB 自带的一个例子来介绍试验模态分析。

详见：https://ww2.mathworks.cn/help/releases/R2021a/ident/ug/modal-analysis-of-a-flexible-flying-wing-aircraft.html

这是明尼苏达大学无人飞行器实验室的小型柔性飞翼飞机的示例。这个例子展示了柔性机翼飞机弯曲模态的计算过程。

通过沿翼型进行机翼的振动响应的多点采集获得数据，用于辨识系统的动态模型。

从辨识出的模型中提取模态参数。

将模态参数数据与传感器位置信息相结合，可视化机翼的各种弯曲模态。

实验设置

实验的目的是收集飞机在外部激励下不同位置的振动响应。

这架飞机悬挂在一个木制框架上，其重心由一根弹簧支撑。该弹簧具有足够的弹性保证弹簧-质量振荡的固有频率不会干扰飞机的基频。通过一个电动激振器在飞机中心附近施加输入力。

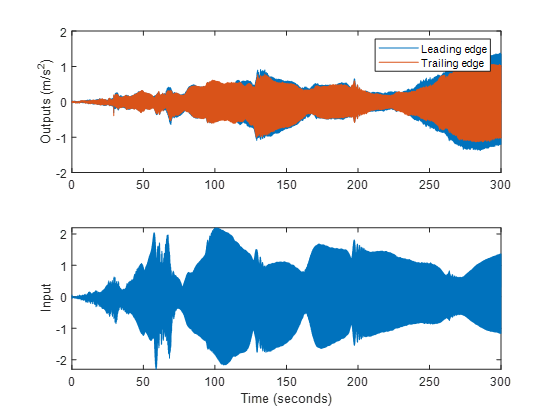
沿着翼展放置 20 个加速度计来收集振动响应，如下图所示

激振器输入命令指定为一个恒定振幅的 chirp 信号 Asin(ω(t)t), chirp 信号的频率随时间线性增加，ω(t)=c0+c1t, 频率范围为 3 - 35hz。试验数据由两个加速度计(在 x 方向的前缘和后缘)一次收集。总共进行了 10 组实验来收集所有 20 个加速度计的响应。加速度计和力传感器的测量频率都是 2000hz。

数据准备

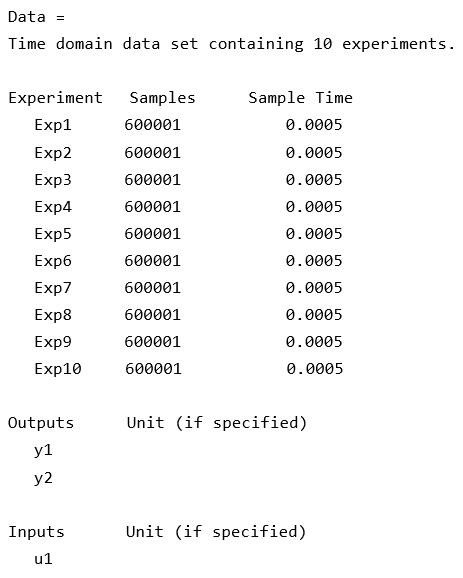
数据由 10 组单输入/双输出信号表示，每组包含 600K 个样本。

变量 MeasuredData 是一个结构体。结构体的每个域还是一个结构体，包含两个响应 y 和对应输入 u。随机绘制第一次实验的数据。

fs = 2000;                % data sampling frequency

Ts = 1/fs;                % sample time

y = MeasuredData.Exp1.y;  % 加速度计的输出值，每个包含两列

u = MeasuredData.Exp1.u;  % input force data

t = (0:length(u)-1)' * Ts;

为了用于系统辨识，将数据封装到 iddata 对象中，并将 10 次试验合并。

Data = merge(Data{:})

系统辨识

我们想识别一个频率响应与实际飞机尽可能接近的动态模型。

动态模型将系统的输入和输出之间的数学关系转化为微分方程或差分方程。例如传递函数和状态空间模型都是动态模型。

动态模型可以通过在时域或频域对试验测量数据运行 fest 和 sest 之类的模型估计命令来创建。

这个例子中，我们先用 etfe 命令进行传递函数估计，从而将测量数据从时域转换为频率响应。然后利用估计的频响函数用于辨识飞机振动响应的状态空间模型。

当然直接利用时域数据进行状态空间模型辨识也是可以的。但频响函数的形式可以将大数据集压缩成更少的样本，并且更方便的在相关的频率范围调整估计过程。

针对每组实验数据（两输出/单输入）进行频响函数(FRF)估算。使用 24000 个频率点进行无窗响应计算。

G = cell(1, 10);

N = 24000;

for k = 1:10

% Convert time-domain data into a FRF using ETFE command

Data_k = getexp(Data, k);

G{k} = etfe(Data_k, [], N); % G{k} is an @idfrd object

end

G = cat(1,G{:});     % 将所有的频响函数合并为一个（20输出/一个输入）的频响

G.OutputName = 'y';   % name outputs 'y1', 'y2', ..., 'y20'

G.InterSample = 'bl';

我们随便挑选第 1 个和第 15 个输出幅值进行绘制来看一下频率响应函数的估计结果。我们关注的频率范围(4 - 35hz)。

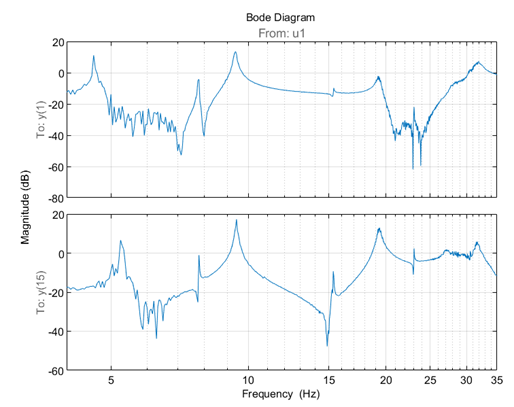
频响函数显示至少 9 个谐振频率(峰值)。我们最关心飞机的机翼弯曲模态，这些模态主要集中在 6- 35hz 的频率范围，因此我们只选择这个范围的频响。

f =G.Frequency/2/pi;           % 单位变换

Gs = fselect(G,f>6 & f<=32)    % 选择频响频率范围 (6.5 - 35 Hz)

接下来，计算一个状态空间模型来逼近 Gs。子空间估计器 n4sid 提供了一个快速的非迭代估计。状态空间模型参数配置会影响精度:

1. 模型阶数的选择。通常要多次尝试。

2. 模型结构。例如是否包含馈通项(状态空间模型中的 D 矩阵是否为零)，等等。

3. 设置权重项，确保低振幅和高振幅对结果有相同的影响。

FRF =squeeze(Gs.ResponseData);

Weighting = mean(1./sqrt(abs(FRF))).';

n4Opt =n4sidOptions('EstimateCovariance',false,...

'WeightingFilter',Weighting,...

'OutputWeight',eye(20));

sys1 = n4sid(Gs,24,'Ts',0,'Feedthrough',true,n4Opt);

Fit = sys1.Report.Fit.FitPercent'

通过查看 Fit 的效果，显示这 20 个响应中最好的和最差的

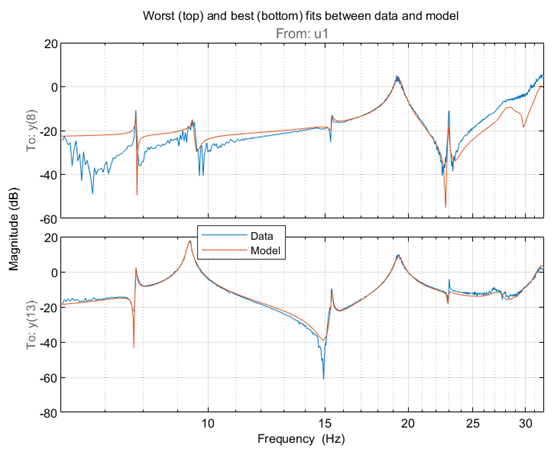
可以看到 sys1 结果仍然有待提高。通过对模型参数进行非线性最小二乘优化迭代，可以进一步改善模型的拟合效果。这可以使用 sest 命令来实现。这一次也估计了参数协方差。

ssOpt = ssestOptions('EstimateCovariance',true,...

'WeightingFilter',n4Opt.WeightingFilter,...

'SearchMethod','lm',...     % use Levenberg-Marquardt search method

'Display','on',...

'OutputWeight',eye(20));

sys2 = ssest(Gs, sys1, ssOpt);  % estimate state-space model (this takesseveral minutes)

Fit = sys2.Report.Fit.FitPercent'

我们同样看看拟合效果：最好的和最差的幅值进行可视化。同时将 1-sd 置信区间可视化出来。

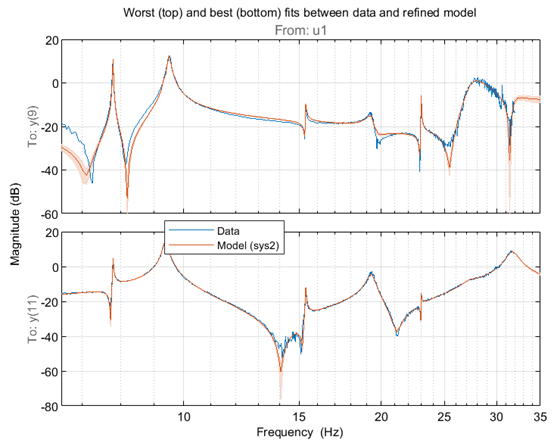
优化后的状态空间模型 sys2 在 7 - 20hz 区域的频响拟合效果很好。多数共振位置的不确定性区间都很窄。我们最开始设置的是一个 24 阶模型，这意味着在系统 sys2 中最多有 12 个谐振模态。使用 modalfit 命令获取这些模态的固有频率。

f = Gs.Frequency/2/pi;     % data frequencies (Hz)

fn = modalfit(sys2, f, 12); % naturalfrequencies (Hz)

fn 中的值表明两个频率非常接近 7.8 Hz，三个接近 9.4 Hz。查看这些频率附近的各点频率响应，峰值位置在输出中确实发生了一些偏移。

这些差异可以通过更好地控制实验过程，直接利用频率为中心的狭窄范围内的时域数据进行直接辨识，或将这些频率附近的频率响应拟合为单个振动模态。本例中不讨论这些替代方案。

模态参数计算

现在我们可以使用模型 sys2 来提取模态参数。通过查看频响结果找到 10 个模态频率，大约在频率 [5 7 10 15 17 23 27 30]Hz 附近左右。通过使用 modalsd 函数可让估计更加准确，该函数尝试不同模型的阶数来检查模态参数的稳定性。

通过稳定图可以看到一组更好的自然响应频率

Freq = [7.8 9.4 15.3 19.3 23.0 27.3 29.231.7];

我们使用 Freq 向量的值作为从模型 sys2 中选择主要模态的基准。使用 modalfit 函数实现

[fn,dr,ms] = modalfit(sys2,f,length(Freq),'PhysFreq',Freq);

fn 是固有频率 (Hz)， dr 是相应的阻尼系数，ms 是模态振型向量 (每个固有频率一列)。

模态振型可视化

我们使用上述模态参数可视化各种弯曲模态。此外，我们需要各测量点位置的信息。

模态振型包含在矩阵 ms 中，其中每一列对应于一个频率的振型。通过在加速度传感器位置坐标上叠加模态振型的振幅并以模态固有频率改变振幅来做动画展示。

结论

这个例子展示了一种基于参数模型辨识的模态参数估计方法。利用 24 阶状态空间模型，在 6 ~ 32 Hz 频率范围内提取了 8 个稳定的振动模态。将模态信息与位置信息相结合，可视化各种弯曲模态。

当然，您也可以对其他设备例如风力发电机的叶片振型进行计算，了解风力机叶片的动态特性从而优化运行效率和预测叶片失效，可以按同样的思路实现。