

无线网络协议的基本架构解析
描述
许多新兴物联网(IoT)无线网络协议的基础是两种基本架构:星形网络和网状网络。
星形网络和网状网络是物联网无线网络的两种基本架构。
随着蓝牙网状网络最近获得关注,网状网络在未来几年可能会变得更加普遍,尤其是在数千个物联网节点必须跨地理区域进行通信的应用中。网状网络可以促进楼宇自动化、能源管理、工业自动化和资产管理等应用。
为了突出网状网络的优点和局限性,本文深入讨论了星形和网状拓扑的基本特征。然后以典型的Zigbee网状网络为例。在以后的文章中,我们将分别研究蓝牙网状网络。
选择合适的物联网无线网络解决方案
物联网应用有几种不同的无线连接解决方案。考虑到广泛的用例,选择正确的无线连接解决方案来满足给定物联网应用的要求可能非常具有挑战性。
在选择连接解决方案时,应考虑范围、数据速率、安全性、功耗和可扩展性等各种因素。
网络拓扑——传感器、执行器和网关节点如何排列或相互连接——是影响网络性能的另一个重要因素。
物联网无线网络的两种基本架构是星形连接和网状连接。
星型拓扑的优缺点
星型拓扑如图1所示。
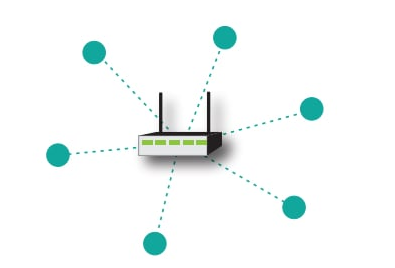
图1.起始地形的高级表示。图片由德州仪器提供
星形网络由所有其他节点连接到的中央集线器组成。节点通过中心集线器相互通信,在大多数情况下,中心集线器也是通往互联网的网关。
家庭Wi-Fi网络是一种熟悉的星型拓扑,其中手机、平板电脑和打印机都连接到中央集线器(无线接入点)。这个中央集线器既可以作为本地网络中的路由器,也可以作为互联网网关。
由于集线器负责沿星形网络分发数据包,因此消息可以通过单个“跳”(节点与集线器之间的数据传输)或两个“跳”(两个节点之间的数据传输)到达目的地。中心)。此功能导致具有一致且可预测的性能的快速网络。
另一个优点是基于星型拓扑的物联网网络可以轻松识别和隔离故障节点,因为每个节点都有自己与集线器的单独连接。
然而,由于数据包必须通过中央节点,网络存在单点故障。如果中心节点发生故障,整个网络将不复存在。
无线星形连接的另一个主要限制是所有节点都应该在中央节点的直接无线电范围内。这限制了网络的物理大小。
此外,星形网络不具备绕过射频障碍物或射频干扰高的环境的灵活性。
网状网络并非如此,它通常在每两个节点之间包含多个路由路径,我们将在稍后讨论。网状网络具有更灵活的布局,更有可能绕过射频障碍物。
网状网络:全网状和部分网状拓扑
在网状网络中,一个节点可以直接与多个其他节点通信。
网状网络有两种类型:全网状和部分网状。
在全网状拓扑中,每个节点都可以与网络中的每个其他节点直接通信。
在部分网状网络中,如图2所示,每个节点可以直接连接到网络中的一个或多个其他节点,但不一定连接到网络中的每个其他节点。
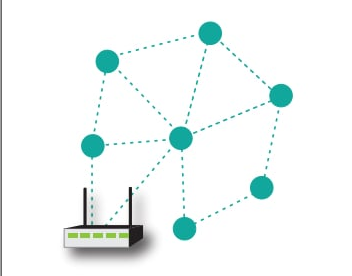
图2.部分网络网格的高级表示。图片由德州仪器提供
物联网应用程序通常使用部分网状拓扑来扩展网络范围,我们将在下面讨论。
在网状网络中,节点可以充当中继器,通过网络路由数据。结果,每两个节点之间有几条不同的路径。这种冗余提高了网络弹性;如果一条路径发生故障,则可以使用替代路径通过网络传播数据。
由于节点能够充当中继器,因此不在彼此直接无线电范围内的节点仍然可以通过路由器节点进行通信。这是物联网应用中网状网络的主要优势,因为它允许用户将网络范围扩展到单个无线电之外。
缺点是通信的多跳特性会增加通过网络传播数据包的延迟。
跳数,因此,网络延迟是数据包通过的路由器数量的函数。这使得评估网络性能比简单的结构(如上面讨论的星形拓扑)更复杂。
在这种情况下,可以使用服务质量(QoS)指标:在指定时间段(例如300毫秒)内到达最终目的地的传输数据包的比率。
网状网络的路由节点应该实现一些路由算法以有效地将数据包传递到目的地。为了实现这些路由功能,路由节点应该有更多的处理能力和内存,这增加了这些节点的复杂性和成本。
星型、树型和网状拓扑的Zigbee协议
Zigbee是一种开放的全球标准,旨在满足低成本、低功耗无线物联网网络的需求。
Zigbee基于IEEE802.15.4链路层,可在2.4GHz、900MHz和868MHz等非授权频段运行。ZigBee支持星形、树形和网状拓扑。
典型的Zigbee网状网络如图3所示。
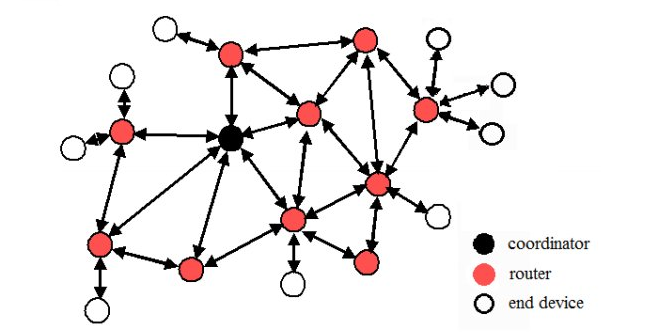
图3 Zigbee网状网络的示例。图片由SMSongWJYao提供
Zigbee网状网络中的无线电扮演着不同的角色。节点可以是协调器、路由器或终端设备。协调器设置网络并允许路由器和终端设备加入网络。除了创建网络之外,协调器还负责管理网络的安全性。
路由器节点总是在监听路由它们通过网络接收到的信息。这些节点通常由电源供电。
最后,终端设备是不路由信息的节点。这些设备保持在睡眠模式以节省电量,并且仅短暂唤醒以轮询其父母并接收已发送给他们的消息。
终端设备通常是电池供电的节点。
Zigbee网状网络可以自动配置自身(自形成)。
此外,当节点离开网络或发生故障时,网络可以根据节点的新组合重新配置路由路径。这种自我修复功能提高了网络在不断变化的条件下的稳定性。
-
移动通信无线网络设计_部分22016-03-15 600
-
TD-SCDMA无线网络优化教程2009-09-18 0
-
如何接入VTache无线网络?2014-03-25 0
-
如何自己写一个无线网络协议2014-10-01 0
-
无线网络2017-07-05 0
-
一种基于Zigbee技术的家用无线网络平台研究2019-07-15 0
-
WIFI无线网络技术有哪些应用范围是什么2021-11-04 0
-
802.11无线网络标准详解2009-08-27 1463
-
无线网络VoIP协议的SDL实现与仿真2009-09-09 572
-
MiWi无线网络协议栈2011-02-10 1443
-
工业无线网络WIA技术解析2012-05-24 4673
-
移动通信无线网络设计_部分32016-03-15 639
-
移动通信无线网络设计_部分12016-03-15 639
-
WCDMA无线网络工程_部分22016-03-31 1045
-
WCDMA无线网络工程_部分12016-03-31 1006
全部0条评论

快来发表一下你的评论吧 !

