

hash表、快排与二分查找:两数之和
描述
今天的题目是两数之和,题目是这样的:
给定一个整数数组与一个target,在数组中找到两个数,其和等于target,并返回这两个数字的下标。
示例:
数组 nums = [2,7,11,15], target = 9,则输出[0,1],因为nums[0] + nums[1] == 9
题目不难,解决方法也有很多种,我们依次来看一下,任何题目都可以从最简单的方法开始去想,以下代码均为C++。
暴力解法
我们首先固定一个数字,比如第一个数字2,然后遍历后面的元素,判断是否相加等于9,有就记录下来,没有则看下一个数字,也就是7,最终代码非常简单,其时间复杂度为O(n^2):
vector twoSum(vector& nums, int target) {
vector res;
for (int i = 0; i < nums.size(); i++) {
for (int j = i + 1; j < nums.size(); j++) {
if (nums[i] + nums[j] == target) {
res.push_back(i);
res.push_back(j);
}
}
}
return res;
}
万万没想到的是这样的代码竟然可以AC(AC是刷题的常用术语,也就是Accept,通过代码的评测标准,包括正确性、耗时、内存的消耗等等)。
从这里的分析我们其实可以知道,这本质上其实是一个搜索问题,假如我知道第一个数字是2,而target是9,那么我们需要回答“这个数组中是否有7这个数字”,因此这本质上是一个搜索问题。
既然是搜索问题,那么hash表显然是我们最得力的武器。
hash 表
关于hash表后续会有专题详解。
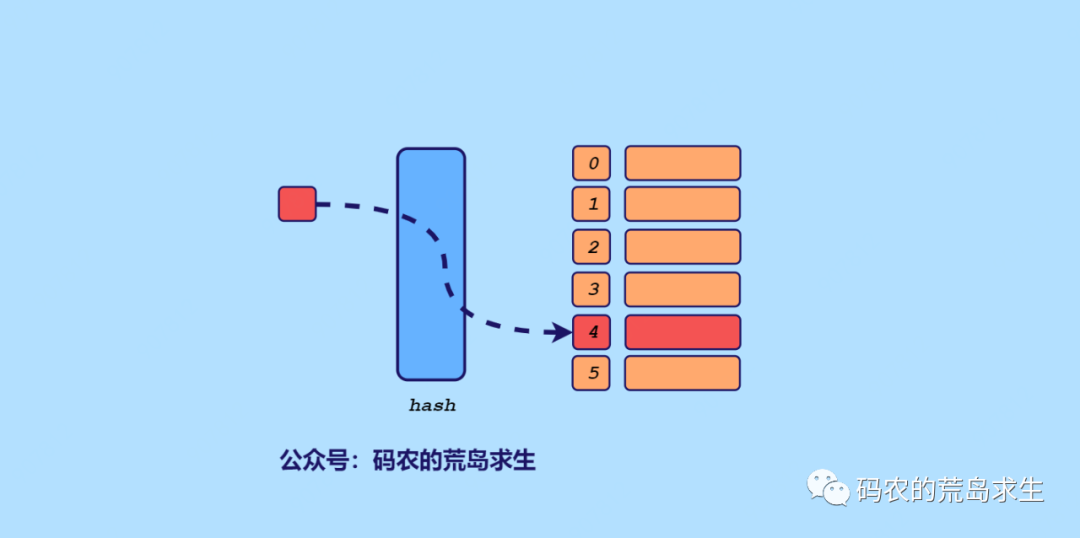
依次遍历数组中每个元素N,查找target-N是否存在于map中即可。
vector twoSum(vector& nums, int target) {
unordered_map map;
vector res;
for (int i = 0; i < nums.size(); i++) {
auto iter = map.find(target - nums[i]);
if (iter == map.end()) {
map[nums[i]] = i;
} else {
res.push_back(i);
res.push_back(iter->second);
}
}
return res;
}
显然,该算法时间复杂度是O(n),因为一般情况下可以认为hash表能常数复杂度下查找到元素。
是不是觉得很简单,注意,这里使用了map容器,那如果面试官要求你不得借助这种已经写的库该怎么办呢?
我们在文章开头分析过,这其实本质上是一个搜索问题,既然是搜索问题,那么解决该问题的另一种思路就是排序。
只要排好序剩下的就简单了,二分查找天然就是有序搜索问题的好帮手。
因此接下来的思路就是排序加二分查找。
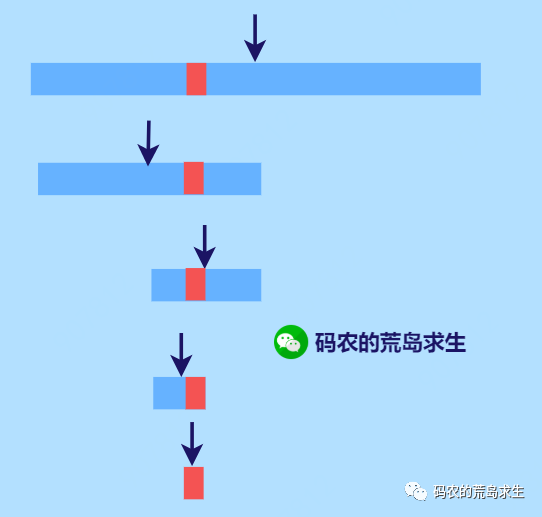
排序加二分查找
思路已经介绍完毕,接下来我们手写快排,但是我们排谁呢?
注意题目要求返回元素下标,因此排序时需要除了数组元素也需要把下标带上。
void quick_sort(vector>& nums, int b, int e) {
if (b > e) return;
int i = b - 1;
for (int k = b; k < e; k++) {
if (nums[k].second < nums[e].second) {
swap(nums[++i], nums[k]);
}
}
swap(nums[++i], nums[e]);
quick_sort(nums, b, i - 1);
quick_sort(nums, i + 1, e);
}
有的同学可能没有看懂这里的排序方法,甚至认为快排之类的排序算法只能靠死记硬背,其实不是的,这类经典的排序算法背后都有极其重要的算法思想,比如快排背后的思想其实是divide and conquer,这是另一个庞大的话题,限于篇幅,我们会在后续专题详解。
现在快排有了,接下来实现二分查找:
int binary_search(vector>& nums,
int b, int e, int target) {
while(b <= e) {
int m = (b + e) / 2;
if (nums[m].second == target) {
return nums[m].first;
} else if (nums[m].second < target) {
b = m + 1;
} else {
e = m - 1;
}
}
return -1;
}
二分查找是一个看起来极其容易但写起来却极其容易出错的算法,不信你可以试试看,这里暂时还不打算详细讲解二分,后续还会多次遇到这个算法,当我们积攒了足够多的示例后将系统介绍这里涉及的快排与二分。
有了这些函数后就可以实现主要逻辑了:
vector twoSum(vector& nums, int target) {
vector res;
vector> nums_index;
int size = nums.size();
for (int i = 0; i < size; i++) {
nums_index.push_back(pair(i, nums[i]));
}
quick_sort(nums_index, 0, size - 1);
for (int i = 0; i < size - 1; i++) {
int r = binary_search(nums_index, i + 1, size - 1,
target - nums_index[i].second);
if (r != -1) {
res.push_back(nums_index[i].first);
res.push_back(r);
}
}
return res;
}
运行一下发现耗时1s左右,虽然也可以AC,但可以看到运行速度其实是很慢的,还是hash表这种解法速度最快。
可以看到,一道题目其实有很多解法,这里涉及到hash、快排与二分查找,后续我们还会多次见到这些方法,而我们在积攒足够多的示例后会系统性讲解这些数据结构与算法。
--- EOF ---审核编辑 :李倩
-
基于Hash和二叉树的路由表查找算法2010-02-22 878
-
正弦波二分频器2009-04-11 4839
-
二分频音乐彩灯威廉希尔官方网站 图2009-06-16 892
-
有源二分频威廉希尔官方网站2009-09-17 6640
-
实现精密二分压威廉希尔官方网站 功能的放大器2012-05-11 5616
-
C语言教程之二分查找2016-04-22 373
-
基于C语言二分查找排序源代码2018-01-04 585
-
图像处理算法之二分查找2018-03-17 4871
-
详解C语言二分查找算法细节2020-06-22 2812
-
二分查找及其变种的总结2021-01-04 2189
-
二分搜索算法运用的框架套路2021-08-25 1836
-
筑基_C_5_对数组的二分查找2021-12-06 340
-
如何理解二分查找算法2023-04-19 622
-
如何用C语言实现高效查找(二分法)2024-06-04 1133
全部0条评论

快来发表一下你的评论吧 !

