

如何使用I/Q信号设计稳健的FSK解码器
描述
一种改进的算法,结合正交调制,可以实现不受相位失准影响的FSK解码。
FSK 符号的频率可以通过检查将接收信号乘以参考信号产生的波形的直流偏移来识别。这是一种简单有效的技术,可以在理想化的数学环境中完美运行,但我们在上一篇文章中看到它对相位失准的鲁棒性不强。
当使用非相干接收机架构时,无法在发射机和接收机之间建立固定的相位关系。这意味着数据包开头的阶段将是不可预测的。仅此一项不会影响我们的解码器算法,因为我们可以使用训练序列来识别解调基带信号的相位,然后相应地修改参考信号。(但是,我对这种方法没有经验,也不知道它在现实生活中的效果如何。)
但是,当我们考虑短期相位变化时,情况会变得更糟,因为这些变化会导致接收信号的相位在一个数据包的空间内偏离参考信号的相位。因此,数据包最初可能具有相位对齐,但恶化的相位关系会产生误码,导致整个数据包被丢弃。
结合正交解调
我在上一篇文章的最后指出了这个问题的解决方案。我们可以使用正交解调来产生 I 和 Q 基带信号,使 FSK 解码算法对相位失准不敏感。
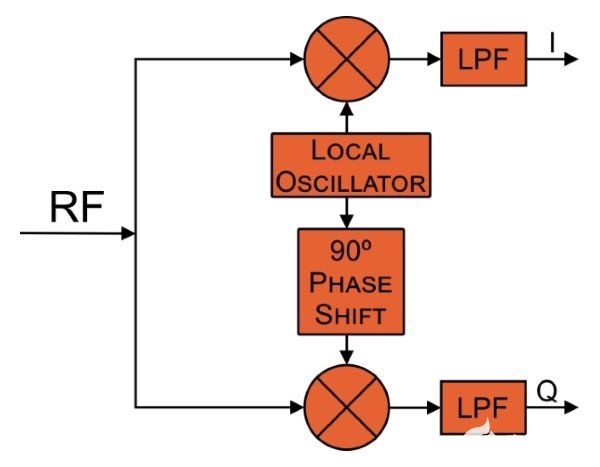
这是对系统非常有益的修改,但这意味着我们需要解调威廉希尔官方网站 中的附加组件(生成 I/Q 信号而不是单个基带信号)和数字信号处理器中的附加时钟周期(因为数学必须是对两个信号而不是一个信号执行)。
第一个问题是相当次要的:正交解调现在非常普遍,我认为在大多数情况下可以采用它而不会显着增加成本、复杂性或 PCB 尺寸。第二个问题的严重性取决于系统的特性。如果您拥有强大的处理器和低数据速率,那么当您结合额外的数学运算时,您可能完全没有问题。但是,如果您选择了低成本、低功耗的处理器并且您正在尝试最大化数据速率,那么所有新的计算都可能使解码算法无法在下一个数据包到达之前完成对一个数据包的处理。
Scilab 中的 I/Q FSK 解码
让我们从建立二进制 0 频率、二进制 1 频率和每个符号的样本数开始,然后我们将根据每个符号的样本数创建索引变量 ( n )。
零频率 = 10e3; 一个频率 = 30e3; 采样频率 = 300e3; Samples_per_Symbol = 采样频率/零频率; n = 0:(Samples_per_Symbol-1);
生成 I/Q 信号
现在我们可以为这两个频率生成 I 和 Q 符号。按照惯例,I(同相)信号是余弦波形,Q(正交)信号是正弦波形。
Symbol_Zero_I = cos(2*%pi*n / (SamplingFrequency/ZeroFrequency)); Symbol_One_I = cos(2*%pi*n / (SamplingFrequency/OneFrequency)); Symbol_Zero_Q = sin(2*%pi*n / (SamplingFrequency/ZeroFrequency)); Symbol_One_Q = sin(2*%pi*n / (SamplingFrequency/OneFrequency)); 子图(2,2,1) 情节(n,Symbol_Zero_I) 子图(2,2,2) 情节(n,Symbol_One_I) 子图(2,2,3) 情节(n,Symbol_Zero_Q) 子图(2,2,4) 情节(n,Symbol_One_Q) f = gcf(); 对于 k=1:4 > f.children(k).font_size = 3; > f.children(k).children.children.thickness = 3; > 结束
(最后的 for 循环会更改每个子图的刻度线标签的大小和每条线的粗细。您可以通过图形窗口中内置的图形界面执行相同的操作;使用 GUI 更直观,但变为一段时间后很累。)
我们的目标是探索相位失调的 I/Q 解决方案,因此我们需要符号的相移版本。如上一篇文章所述,接收信号和参考信号之间的最坏情况相位差为 90°,因此我们将生成相位为 45°(即完美对齐和最坏情况对齐的中间)和 90° 的符号.
Symbol_Zero_I_45deg = cos(%pi/4 + 2*%pi*n / (SamplingFrequency/ZeroFrequency)); Symbol_One_I_45deg = cos(%pi/4 + 2*%pi*n / (SamplingFrequency/OneFrequency)); Symbol_Zero_Q_45deg = sin(%pi/4 + 2*%pi*n / (SamplingFrequency/ZeroFrequency)); Symbol_One_Q_45deg = sin(%pi/4 + 2*%pi*n / (SamplingFrequency/OneFrequency)); Symbol_Zero_I_90deg = cos(%pi/2 + 2*%pi*n / (SamplingFrequency/ZeroFrequency)); Symbol_One_I_90deg = cos(%pi/2 + 2*%pi*n / (SamplingFrequency/OneFrequency)); Symbol_Zero_Q_90deg = sin(%pi/2 + 2*%pi*n / (SamplingFrequency/ZeroFrequency)); Symbol_One_Q_90deg = sin(%pi/2 + 2*%pi*n / (SamplingFrequency/OneFrequency));
现在让我们为二进制序列 0101 创建三组 I 和 Q 基带信号。
Baseband_I_aligned = [Symbol_Zero_I Symbol_One_I Symbol_Zero_I Symbol_One_I]; Baseband_Q_aligned = [Symbol_Zero_Q Symbol_One_Q Symbol_Zero_Q Symbol_One_Q]; Baseband_I_45deg = [Symbol_Zero_I_45deg Symbol_One_I_45deg Symbol_Zero_I_45deg Symbol_One_I_45deg]; Baseband_Q_45deg = [Symbol_Zero_Q_45deg Symbol_One_Q_45deg Symbol_Zero_Q_45deg Symbol_One_Q_45deg]; Baseband_I_90deg = [Symbol_Zero_I_90deg Symbol_One_I_90deg Symbol_Zero_I_90deg Symbol_One_I_90deg]; Baseband_Q_90deg = [Symbol_Zero_Q_90deg Symbol_One_Q_90deg Symbol_Zero_Q_90deg Symbol_One_Q_90deg]; 子图(3,2,1) 情节(Baseband_I_aligned) 子图(3,2,2) 情节(Baseband_Q_aligned) 子图(3,2,3) 绘图(Baseband_I_45deg) 子图(3,2,4) 绘图(Baseband_Q_45deg) 子图(3,2,5) 情节(基带_I_90度) 子图(3,2,6) 绘图(Baseband_Q_90deg) f = gcf(); 对于 k=1:6 > f.children(k).font_size = 3;
> 结束
I/Q 乘法
我们现在可以将相位对齐和相移的 I/Q 基带信号乘以参考符号。尽量不要被一长串的计算分心;我们所做的只是将 I 和 Q 波形首先乘以二进制 0 符号的等长数组,然后乘以二进制 1 符号的等长数组。但是,我们必须这样做 3 次,因为我们想要比较相位对齐版本、相位 = 45° 版本和相位 = 90° 版本的结果。这并不反映将由数字信号处理器执行的实现——在实际应用中将只有一个 I/Q 基带信号。
请注意,这里我使用 I 符号作为参考符号,但我也可以使用 Q 符号。实际上,我可以使用具有任何相位值的参考符号:通过将 I/Q 技术结合到此解码算法中,我们使该过程对接收符号和参考符号之间的任何类型的相位差异都不敏感。
DecodeZero_I_aligned = Baseband_I_aligned .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I]; DecodeZero_Q_aligned = Baseband_Q_aligned .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I]; DecodeOne_I_aligned = Baseband_I_aligned .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I]; DecodeOne_Q_aligned = Baseband_Q_aligned .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I]; DecodeZero_I_45deg = Baseband_I_45deg .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I]; DecodeZero_Q_45deg = Baseband_Q_45deg .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I]; DecodeOne_I_45deg = Baseband_I_45deg .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I]; DecodeOne_Q_45deg = Baseband_Q_45deg .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I]; DecodeZero_I_90deg = Baseband_I_90deg .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I]; DecodeZero_Q_90deg = Baseband_Q_90deg .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I]; DecodeOne_I_90deg = Baseband_I_90deg .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I]; DecodeOne_Q_90deg = Baseband_Q_90deg .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I];
下图显示了乘法产生的波形。
子图(2,2,1) 情节(DecodeZero_I_aligned) 子图(2,2,2) 情节(DecodeZero_Q_aligned) 子图(2,2,3) 情节(DecodeOne_I_aligned) 子图(2,2,4) 情节(DecodeOne_Q_aligned)
子图(2,2,1)
情节(DecodeZero_I_45deg)
子图(2,2,2)
情节(DecodeZero_Q_45deg)
子图(2,2,3)
情节(DecodeOne_I_45deg)
子图(2,2,4)
情节(DecodeOne_Q_45deg)
子图(2,2,1)
情节(DecodeZero_I_90deg)
子图(2,2,2)
情节(DecodeZero_Q_90deg)
子图(2,2,3)
情节(DecodeOne_I_90deg)
子图(2,2,4)
情节(DecodeOne_Q_90deg)
结论
如果您仔细思考最后一组图,我想您将开始了解 I/Q 处理在 FSK 解码上下文中的好处。由于输入信号的相位与参考符号的相位失去对齐,因此作为接收频率与参考频率之间相似性的指标,乘法波形的 DC 偏移变得不可靠。然而,90°相移基带信号的存在弥补了这种影响,因为当一个基带信号的相位差接近±90°(最坏情况)时,另一个基带信号的相位接近0°或 180°(最佳情况)。
-
ESS的ES9311Q 音响、功放、解码器2019-11-27 0
-
怎么理解真正的编码器和解码器?2020-09-01 0
-
来电解码器及其在客户关系管理中的应用2010-08-03 460
-
CML推出DTMF编解码器/FSK调制解调器复合IC2006-03-13 852
-
常用DTMF/FSK解码器集成威廉希尔官方网站2006-06-30 3322
-
什么是音频编解码器?2009-05-03 4050
-
立体声电视解码器Ⅰ2009-10-08 1021
-
dmx512解码器怎么接线?dmx512解码器接线图2017-12-06 88838
-
高清解码器的作用2018-12-10 13185
-
G.711附录I,带PLC的语音编解码器-下载产品代码2021-03-23 670
-
ADP5585:键盘解码器和I/O扩展数据表2021-05-27 587
-
ADP5589:键盘解码器和I/O扩展数据表2021-05-27 514
-
1-of-4 解码器/解复用器-HEF4555B_Q1002023-02-09 227
-
光栅解码器损坏的表现有哪些2024-09-23 550
-
遥控器解码器怎么使用2024-09-30 873
全部0条评论

快来发表一下你的评论吧 !

