

Python实现所有算法:拉夫逊方法
描述
emmmmm,好长时间没有用matplotlib,都不会画图了。先绘制一个x**3-1的函数,然后考虑在a,b之间找他的根。
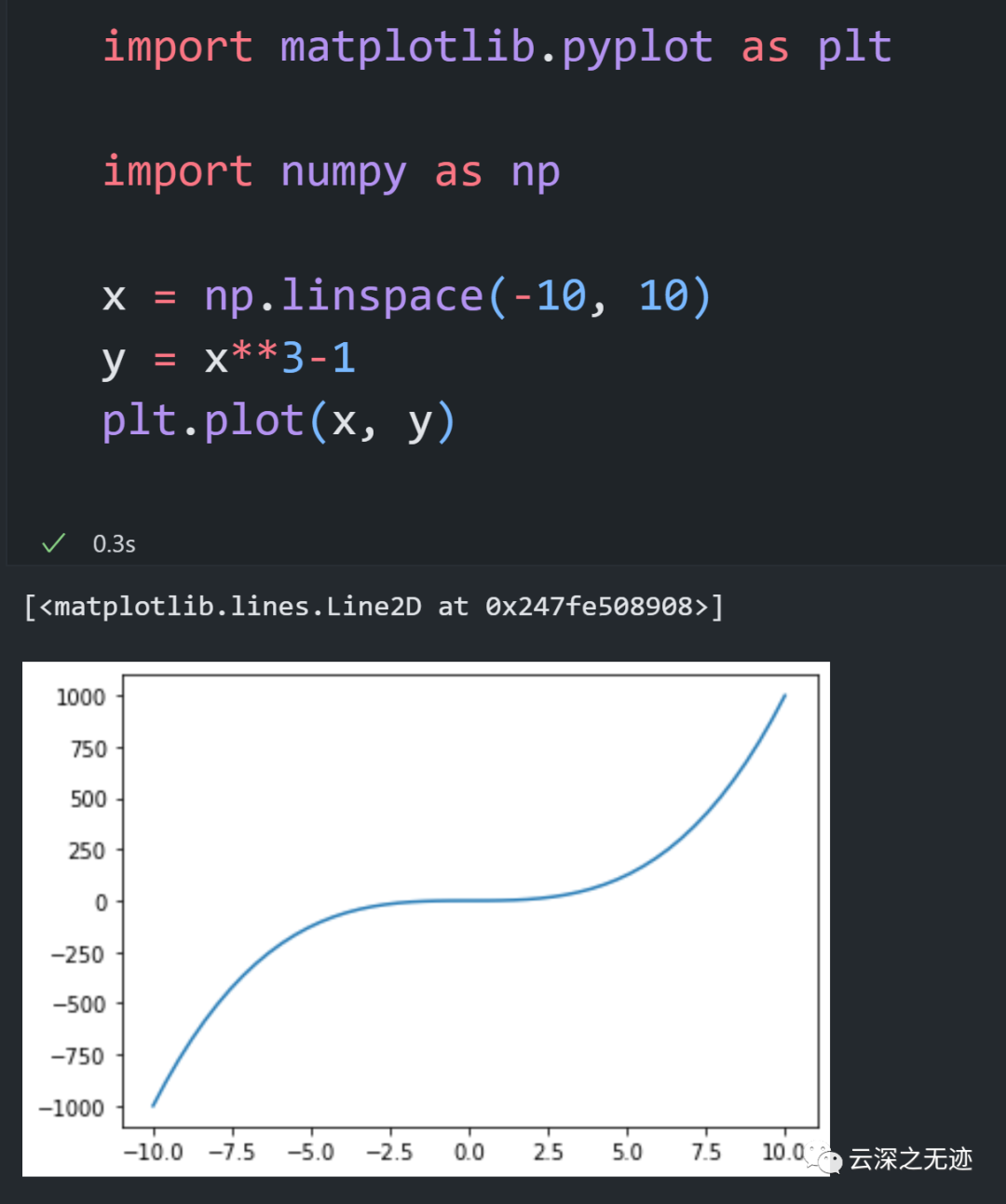
-10,10
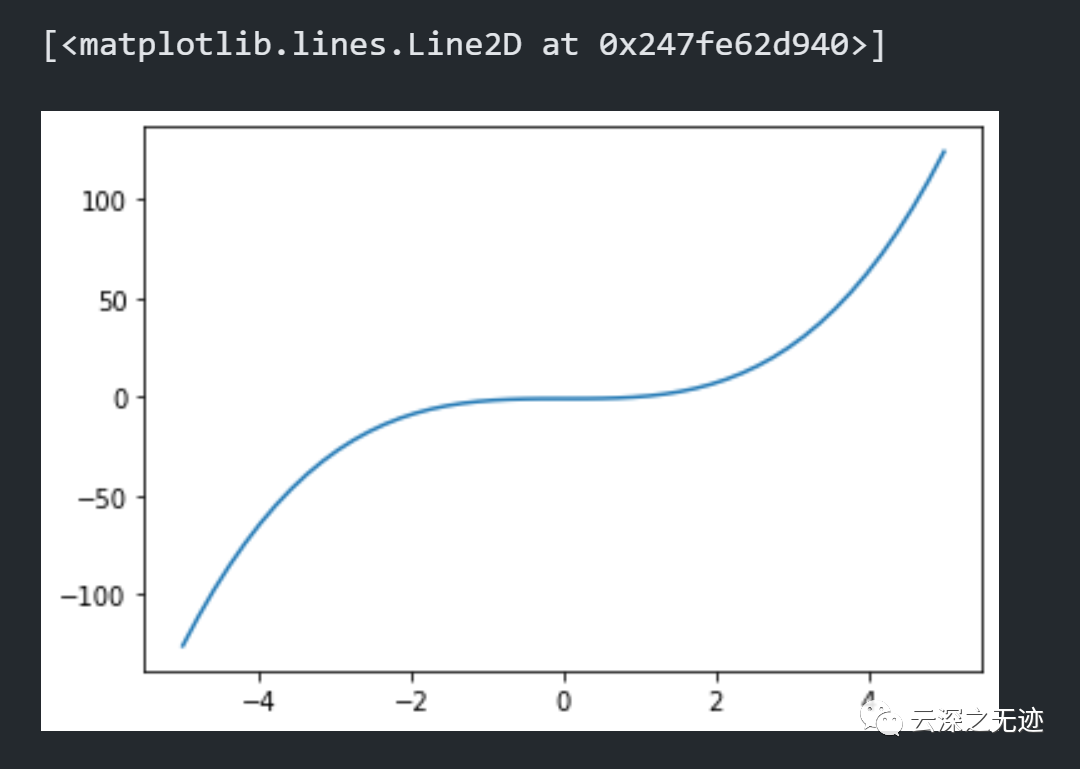
-5,5
那么这个函数被起名为intersection
连续函数与x相交时就是根,是不是很形象。
def intersection(function: Callable[[float], float], x0: float, x1: float) -> float:
因为我们知道,这个函数应该是我们给出要求解的区间和函数给出一个根。那么这里function的Callable就是可以当匿名函数传递。

为了函数的灵活性,这里使用float

主函数,因为我们函数其实不知道具体的函数的循环次数,那么就可以使用while的循环。
一开始要判断参数的情况,如果都相等,你这算啥???以及都带进去,再算一下,双保险,双重扑街。
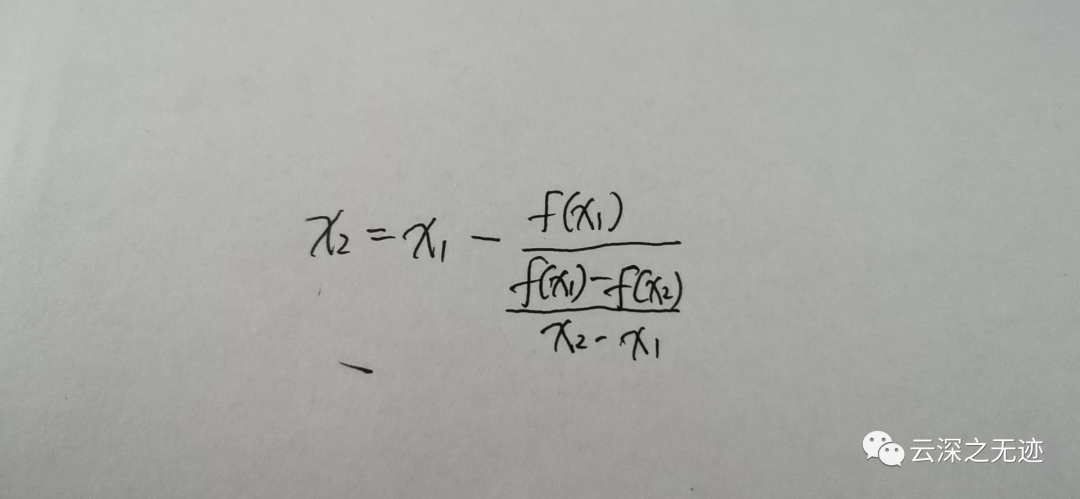
接下来就是这个公式,我是个罪人,用了一张A4纸就写一个这
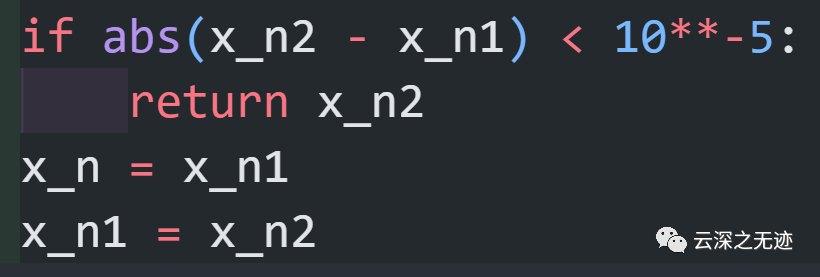
计算的X看看符合要求吗?不符合就继续将值域缩小。直到很小。
这个不是二分法,但是差不多的意思,不过这个是牛顿法,也叫牛顿-拉夫逊(拉弗森)方法,就我的题目。
这篇文章的下面就讲讲这个东西:
它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
多数方程不存在求根公式,因此求精确根非常困难,甚至不可解,从而寻找方程的近似根就显得特别重要。方法使用函数 f(x) 的泰勒级数的前面几项来寻找方程 f(x)=0 的根。牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程 f(x)=0 的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时线性收敛,但是可通过一些方法变成超线性收敛。

牛!
迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法(或者称为一次解法),即一次性解决问题。迭代算法是用计算机解决问题的一种基本方法。它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。
利用迭代算法解决问题,需要做好以下三个方面的工作:
一、确定迭代变量
在可以用迭代算法解决的问题中,至少存在一个可直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
二、建立迭代关系式
所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系)。迭代关系式的建立是解决迭代问题的关键,通常可以使用递推或倒推的方法来完成。
三、对迭代过程进行控制
在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。不能让迭代过程无休止地执行下去。迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来;另一种是所需的迭代次数无法确定。对于前一种情况,可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况,需要进一步分析得出可用来结束迭代过程的条件。

然后,自己的函数也可以这样定义
intersection(f, 3, 3.5)
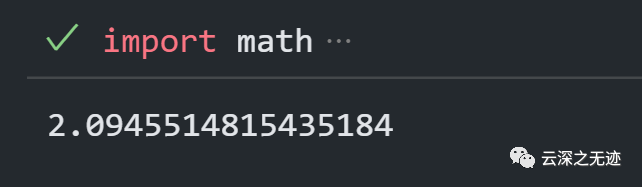
精度ok
再说说数值求法:
大多数的数值求根算法都使用迭代法,生成一个以方程的根为极限的收敛数列。它们需要一个或多个根作为迭代的初期值,之后每次迭代都生成一个逐步逼近根的值。
由于迭代法必须在有限步内终止于某个点,这些方法都只能提供一个根的近似值,而不能提供一个精确解。许多方法是通过代入上一个迭代值来计算一个辅助方程,从而得出下一个迭代值的。此处所指的辅助方程是指为了使原方程的根是一个定点并使迭代值能更快地收敛到这些定点而设计的一个方程,因此迭代值的极限是这个辅助方程的一个定点。
求根算法的性能是数值分析的研究范畴。一种算法的效率可能大幅度取决于已知点的性质。
例如,一部分算法都使用输入函数的导数(此要求函数不但连续,而且可导),而其他算法则能用于任何一个连续函数。在一般情况下,数值算法不能保证找到一个函数的所有根,因此算法未能找到根并不能证明方程无根。然而,对于多项式,存在特定的使用代数学性质以定位根的所在区间(或复根所在的圆盘)的算法,这个区间(或圆盘)足够小以能保证数值算法(例如牛顿法)能收敛到唯一被定位的根。
-
实现狄克逊准则2016-03-24 0
-
Python实现k-近邻算法2018-10-10 0
-
利用python实现KNN算法2019-10-25 0
-
Python的Apriori算法和FP-Growth算法是什么2020-06-04 0
-
KNN分类算法及python代码实现2020-06-05 0
-
BP神经网络算法 python实现2017-12-29 21518
-
蚁群算法python编程实现2018-02-02 7467
-
简单潮流计算的牛顿拉夫逊程序2018-03-05 877
-
使用Python实现所有算法2022-07-06 985
-
Python实现所有算法-基本牛顿法2022-07-13 1646
-
[源代码]Python算法详解2023-06-06 299
-
基于Python实现随机森林算法2023-09-21 1208
全部0条评论

快来发表一下你的评论吧 !

