这种匹配（消除）问题也是栈的擅长所在！

844.比较含退格的字符串

给定 S 和 T 两个字符串，当它们分别被输入到空白的文本编辑器后，判断二者是否相等，并返回结果。# 代表退格字符。

注意：如果对空文本输入退格字符，文本继续为空。  示例 1：

• 输入：S = "ab#c", T = "ad#c"
• 输出：true
• 解释：S 和 T 都会变成 “ac”。

示例 2：

• 输入：S = "ab##", T = "c#d#"
• 输出：true
• 解释：S 和 T 都会变成 “”。

示例 3：

• 输入：S = "a##c", T = "#a#c"
• 输出：true
• 解释：S 和 T 都会变成 “c”。

示例 4：

• 输入：S = "a#c", T = "b"
• 输出：false
• 解释：S 会变成 “c”，但 T 仍然是 “b”。

思路

本文将给出 空间复杂度O(n)的栈模拟方法 以及空间复杂度是O(1)的双指针方法。

普通方法（使用栈的思路）

这道题目一看就是要使用栈的节奏，这种匹配（消除）问题也是栈的擅长所在，跟着一起刷题的同学应该知道，在栈与队列：匹配问题都是栈的强项，我就已经提过了一次使用栈来做类似的事情了。

那么本题，确实可以使用栈的思路，但是没有必要使用栈，因为最后比较的时候还要比较栈里的元素，有点麻烦。

这里直接使用字符串string，来作为栈，末尾添加和弹出，string都有相应的接口，最后比较的时候，只要比较两个字符串就可以了，比比较栈里的元素方便一些。

代码如下：

class Solution {
public:
    bool backspaceCompare(string S, string T) {
        string s; // 当栈来用
        string t; // 当栈来用
        for (int i = 0; i < S.size(); i++) {
            if (S[i] != '#') s += S[i];
            else if (!s.empty()) {
                s.pop_back();

        }
        for (int i = 0; i < T.size(); i++) {
            if (T[i] != '#') t += T[i];
            else if (!t.empty()) {
                t.pop_back();
            }
        }
        if (s == t) return true; // 直接比较两个字符串是否相等，比用栈来比较方便多了
        return false;
    }
};

• 时间复杂度:O(n + m)， n为S的长度，m为T的长度 ，也可以理解是O(n)的时间复杂度
• 空间复杂度:O(n + m)

当然以上代码，大家可以发现有重复的逻辑处理S，处理T，可以把这块公共逻辑抽离出来，代码精简如下：

class Solution {
private:
string getString(const string& S) {
    string s;
    for (int i = 0; i < S.size(); i++) {
        if (S[i] != '#') s += S[i];
        else if (!s.empty()) {
            s.pop_back();
        }
    }
    return s;
}
public:
    bool backspaceCompare(string S, string T) {
        return getString(S) == getString(T);
    }
};

性能依然是：

• 时间复杂度:O(n + m)
• 空间复杂度:O(n + m)

优化方法（从后向前双指针）

当然还可以有使用 O(1) 的空间复杂度来解决该问题。

同时从后向前遍历S和T（i初始为S末尾，j初始为T末尾），记录#的数量，模拟消除的操作，如果#用完了，就开始比较S[i]和S[j]。

动画如下：

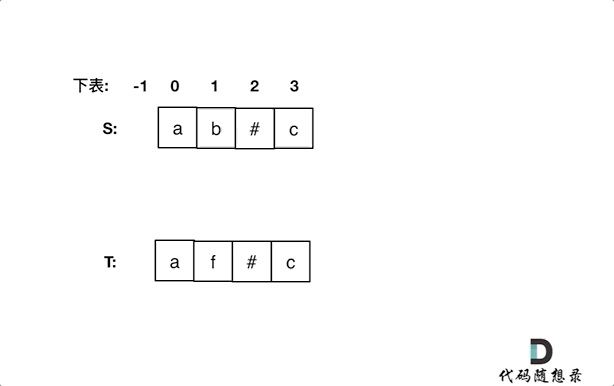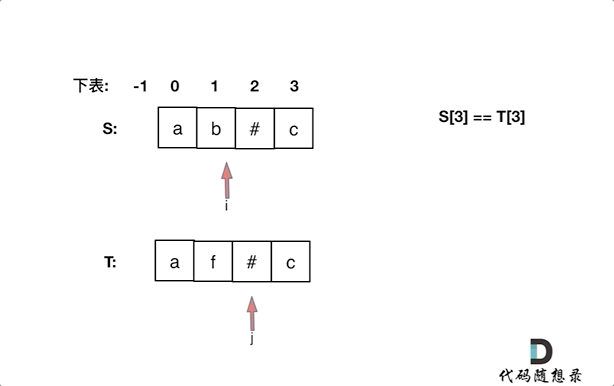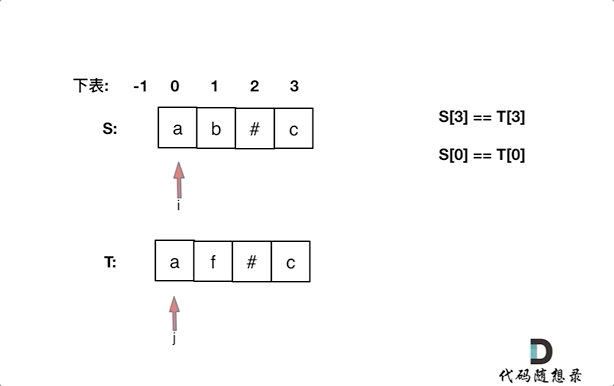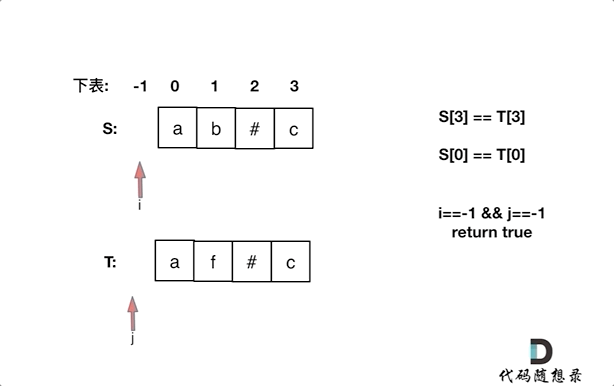
如果S[i]和S[j]不相同返回false，如果有一个指针（i或者j）先走到的字符串头部位置，也返回false。

代码如下：

class Solution {
public:
    bool backspaceCompare(string S, string T) {
        int sSkipNum = 0; // 记录S的#数量
        int tSkipNum = 0; // 记录T的#数量
        int i = S.size() - 1;
        int j = T.size() - 1;
        while (1) {
            while (i >= 0) { // 从后向前，消除S的#
                if (S[i] == '#') sSkipNum++;
                else {
                    if (sSkipNum > 0) sSkipNum--;
                    else break;
                }
                i--;
            }
            while (j >= 0) { // 从后向前，消除T的#
                if (T[j] == '#') tSkipNum++;
                else {
                    if (tSkipNum > 0) tSkipNum--;
                    else break;
                }
                j--;
            }
            // 后半部分#消除完了，接下来比较S[i] != T[j]
            if (i < 0 || j < 0) break; // S 或者T 遍历到头了
            if (S[i] != T[j]) return false;
            i--;j--;
        }
        // 说明S和T同时遍历完毕
        if (i == -1 && j == -1) return true;
        return false;
    }
};

• 时间复杂度：O(n + m)
• 空间复杂度：O(1)