

数字二进制计数器的设计和实现
今日头条
描述
将二进制数视为元胞自动机可能有助于数字二进制计数器的设计和实现吗?
正如大多数读者已经知道的那样,二进制计数类似于任何其他数字系统中的计数。计数从使用下一个可用符号(十进制的 0 到 9,八进制的 0 到 8,十六进制的 0 到 F,二进制的 0 和 1)增量替换最低有效位(最右边的位置)开始。当这个数字的符号用尽时(因为最后一个符号已经被使用),这个最低有效数字被重置为 0 并且左边的数字增加。此过程以迭代方式继续,因此当任何位置的数字符号用尽时,该数字重置为 0,并且其左侧的数字递增。
我们刚刚在上面所做的是设置了一个规则,用于计算或从一个数字演变为下一个数字。一个数字可以被认为是一个n位的一维数组(在二进制的情况下称为“位”),其中用于一个数字的下一个符号不仅取决于该数字的当前符号,还取决于在数组中其他数字的当前符号上。基于此,我开始怀疑将二进制数视为元胞自动机是否有助于数字二进制计数器的设计和实现。
编者注:从 Conway 的生命游戏到 Langton 的蚂蚁再到 Reynold 的 Boids,人工生命模拟展示了由简单规则引起的复杂紧急行为(另见“人工生命模拟”)。
很明显,如果不知道元胞自动机是什么以及它如何与数字数组相关,我将无法对此感到疑惑,但是当我们阅读以下元胞自动机的简明一般定义时,这种关系变得显而易见:
一个规则的细胞网格,其特征是有限数量的状态,这些状态将根据一些固定规则(进化)从当前变化(进化)到下一代,该规则根据两者的当前状态确定每个细胞的新状态单元格和其他单元格(其邻域)。
在二进制数的情况下,位等价于单元格,可能的状态是 0 和 1,自动机是一维的(上面的网格只有一行,因为只有一个数组要考虑),以及任何生成的自动机表示与其所有位的状态相对应的数字。
一维元胞自动机的一个特例是所谓的初等元胞自动机,其中每个元胞只能有两个状态,并且下一代每个元胞的状态仅取决于元胞及其两个直接邻居的当前状态(右边和左边)。这种基本元胞自动机的一个例子就是规则 90,其中所有单元的状态同时被它们的两个相邻单元的状态的异或 (XOR) 替换。

图 1:具有随机初始条件的规则 90 的时空图(来源:Javier Piay)
当从单个活细胞(只有一个细胞的状态为 1)开始时,规则 90 具有谢尔宾斯基三角形形式的时空图(随时间演变的一维数组)。
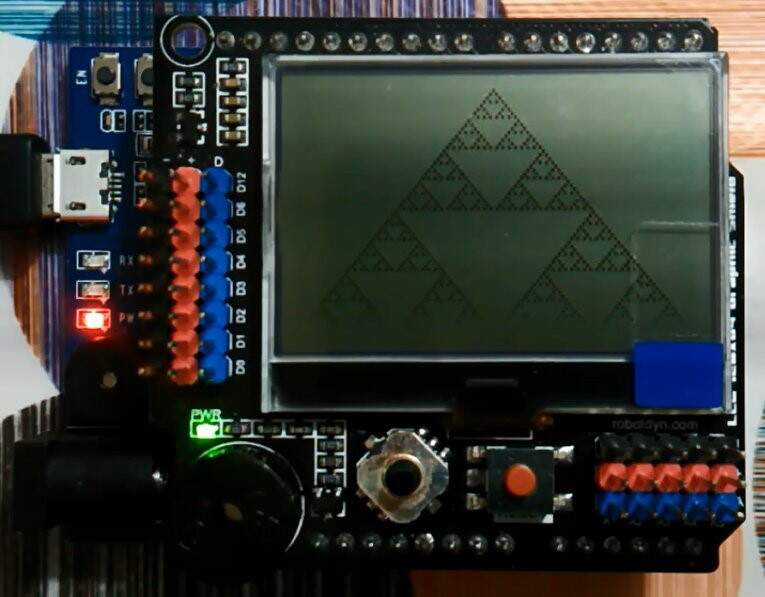
图 2:规则 90 的时空图从单个活细胞开始,形成谢尔宾斯基三角形。(来源:哈维尔皮耶)
在本视频中,您将找到一些我为三个计算机平台创建的规则 90 自动机动画:micro:bit、Arduino 和我的SANX-I 微型计算机。
就受欢迎程度和学术/科学兴趣而言,约翰康威创造的生命游戏元胞自动机排名第一。康威的生命游戏是一个二维元胞自动机,其中每个细胞根据一些简单的方法与其八个邻居相互作用进化规律如下:
任何少于两个活邻居的活细胞都会死亡,就像人口不足一样。
任何有两三个活邻居的活细胞都可以活到下一代。
任何有超过三个活邻居的活细胞都会死亡,就像人口过剩一样。
任何只有三个活邻居的死细胞都会变成活细胞,就像通过繁殖一样。
生命游戏自动机产生许多不同类型的动画、意想不到和不可预测的模式(如静物、振荡器和宇宙飞船),即使是那些偶然发现它的人中最不好奇的人也会对这种细胞自动机着迷。我还编写了程序来模拟不同平台上的生命游戏,并从随机初始配置(生成)和特定配置开始探索这些动画模式。在此视频中,您将找到我的 Arduino 生命游戏。
在这个视频中,你会发现我的 micro:bit 生命游戏:
到目前为止,一切都很好(我希望)。
现在,如果您回想本专栏的开头,您会记得本文的真正目的是确定将二进制数视为元胞自动机是否有助于数字二进制计数器的设计和实现。我们已经知道,我们正在寻找的元胞自动机将是一维的,但不是基本类型,因为下一代细胞/数字/位的状态不仅仅取决于细胞的当前状态及其两个直接邻居。实际上,该状态似乎仅取决于其右侧邻居的当前状态。你怎么看?
如果你仔细看计数规则,你会发现这是一个迭代过程,其中一个数字的下一个值不仅取决于它自己的值和它右边数字的值,还取决于数字的值在其右侧的数字的右侧。这个迭代过程或依赖关系一直持续到数组的最右边(最低有效位)。换句话说,一个数字的下一个值取决于它自己的值和它右边所有数字的值。
当我得出这个结论时,我首先认为这样的自动机会比基本自动机复杂得多(其中一个单元仅受其两个相邻邻居的影响);此外,很难设定和实施进化(计数)规则。幸运的是,我意识到这种对几个单元格(实际上是右边的所有单元格)的依赖可以转换为对右边相邻单元格的依赖,从而产生一种“简化和修改的基本自动机”。
只需向每个单元格(除了其二进制状态)添加一个新属性或 FLAG 即可轻松完成此转换,其值仅由其右侧的单元格修改。当其右边所有单元的状态为 1 时,该 FLAG 将为 1,这意味着自动机满足进化规则,因此,单元的下一个状态将从 0 变为(反转)为 1,或从 1 到 0,根据本文第一段中描述的增量替换过程(二进制增量)。如前所述,这个FLAG的值只会被右边的单元格修改;因此,当且仅当此单元状态的当前状态值和与右侧单元关联的 FLAG 的值都为 1 时,它将被设置为 1。
如前所述,我称这个元胞自动机为“简化的”和“修改的”基本自动机——“简化”是因为任何单元格(受影响的单元格)的邻域都被简化为右侧的单元格并被“修改”,因为每个单元格都具有特征不仅取决于它的状态,还取决于它的 FLAG。
只要一个或多个细胞满足进化规则(将它们的 FLAG 设置为 1),这个自动机就会进化。但是要让这个自动机能够持续进化,最右边的细胞必须始终满足进化规则所施加的要求;否则,一旦该单元的状态变为 0,进化将停止。因此,最右边的单元将连接到其右侧称为 ENABLE 的外部输入。如果 ENABLE 为 TRUE(或 1),自动机将进化(执行二进制计数);否则,所有后续世代都将保持不变。
从当前一代到下一代的进化将由从最右边的单元到最左边的单元级联的外部时钟信号控制。
对于初始或第一代,任何单元格中都允许任何状态(0/1)。但是,出于演示目的,我们将首先将所有单元格清除为初始状态 0。
正如你们中最有洞察力的人现在可能意识到的那样(正如托比魔鬼——罗文·阿特金森爵士扮演的角色——可能会说的那样),这个自动机可以通过级联连接来实现,我称之为“基本单元”。
这个基本单元有两个输入和两个输出。任何单元的输入都将连接到其右侧邻居的输出,而任何单元的输出将连接到其左侧邻居的输入。
每个单元的输入之一将是 CLOCK 信号,另一个将由其右邻居使用来修改其 FLAG。同样,每个单元的输出之一将是 CLOCK 信号,而另一个将用于修改其左侧单元的 FLAG。
图 3 显示了基本单元的数字电子实现,使用一个 D 型触发器来存储其当前状态,一个 XOR 门在其 FLAG 设置为 1 时更改(反转)其状态,以及一个 AND 门来设置当它的状态和它的 FLAG 都为 1 时,它左边的单元格的 FLAG 为 1。
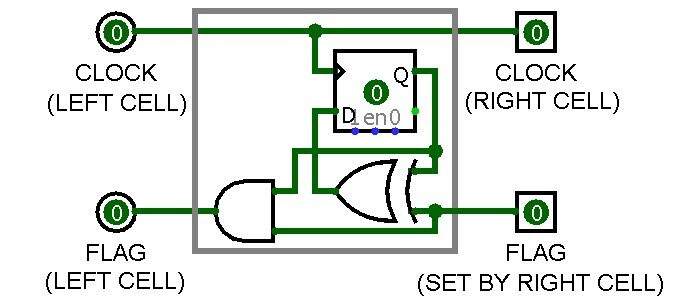
图 3:自动机基本单元(来源:Javier Piay)
图 4 显示了最右边的基本单元,其输入连接到外部 CLOCK 和 ENABLE 信号。
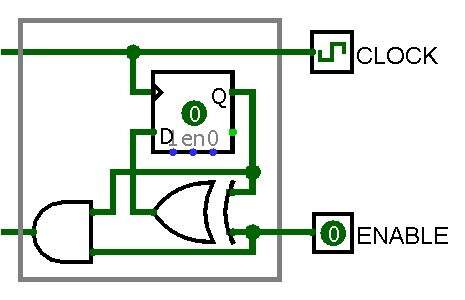
图 4:Automaton 最右边的基本单元(来源:Javier Piay)
现在一切都准备就绪,可以互连五个单元,如图 5 所示:

图 5:五细胞自动机(来源:Javier Piay)
现在,看看这个视频,来验证这个经过简化和修改的基本元胞自动机实际上是否像一个 5 位二进制计数器一样进化。
既然我们已经到了本文的结尾,我希望您对这种基于元胞自动机的方法是否有助于二进制计数器的设计和实现有自己的答案。我猜你已经知道我的回答是“是的”(至少,这是给我的)。
如果您的任务是设计和实现这个数字逻辑系统,请不要犹豫,让我知道您最有可能遵循的其他程序或方法。像往常一样,我们非常欢迎您的回答、问题或评论。
审核编辑:汤梓红
-
TTL二进制同步可逆计数器2009-08-03 667
-
12位二进制计数器2009-09-16 6430
-
异步二进制计数器2009-09-30 15163
-
同步二进制计数器2009-09-30 12172
-
什么是二进制计数器,二进制计数器原理是什么?2010-03-08 31103
-
3位二进制计数器2017-11-08 1741
-
二进制加计数器浅析2017-11-24 1049
-
12级二进制纹波计数器-HEF4040B2023-02-15 318
-
14级二进制纹波计数器-74HC_HCT40202023-02-15 283
-
12级二进制纹波计数器-74HC_HCT40402023-02-16 309
-
双4位同步二进制计数器-74HC_HCT45202023-02-17 702
-
7级二进制纹波计数器-74HC4024_Q1002023-02-21 286
-
8位同步二进制递减计数器-74HC401032023-03-03 700
-
构建LED二进制计数器2023-06-12 526
-
二进制串行计数器工作原理是什么?2024-05-28 838
全部0条评论

快来发表一下你的评论吧 !

