

meta reweighting 策略来增强伪样本的效果
描述
自增强(self-augmentation)最近在提升低资源场景下的 NER 问题中得到了越来越多的关注,token 替换和表征混合是对于 NER 这类 token 级别的任务很有效的两种自增强方法。值得注意的是,自增强的方法得到的增强数据有潜在的噪声,先前的研究是对于特定的自增强方法设计特定的基于规则的约束来降低噪声。
本文提出了一个联合的 meta-reweighting 的策略来自然的进行整合。我们提出的方法可以很容易的扩展到其他自增强的方法中,实验表明,本文的方法可以有效的提升自增强方法的表现。

命名实体识别旨在从非结构化文本中抽取预先定义的命名实体,是 NLP 的一个基础任务。近期,基于神经网络的方法推动 NER 任务不断取得更好的表现,但是其通常需要大规模的标注数据,这在真实场景中是不现实的,因此小样本设置的 NER 更符合现实需求。
数据自增强是一个小样本任务可行的解法,对于 token-level 的 NER 任务,token 替换和表征混合是常用的方法。但自增强也有局限性,我们需要为每种特定的自增强方法单独进行一些设计来降低自增强所带来的噪声,缓解噪声对效果的影响。本文提出了 meta-reweighting 框架将各类方法联合起来。
首先,放宽前人方法中的约束,得到更多伪样本。然而这样会产生更多低质量的增强样本,为此,我们提出 meta reweighting 策略来控制增强样本的质量。同时,使用 example reweighting 机制可以很自然的将两种方法结合在一起。实验表明,在小样本场景下,本文提出的方法可以有效提升数据自增强方法的效果,在全监督场景下本文的方法仍然有效。
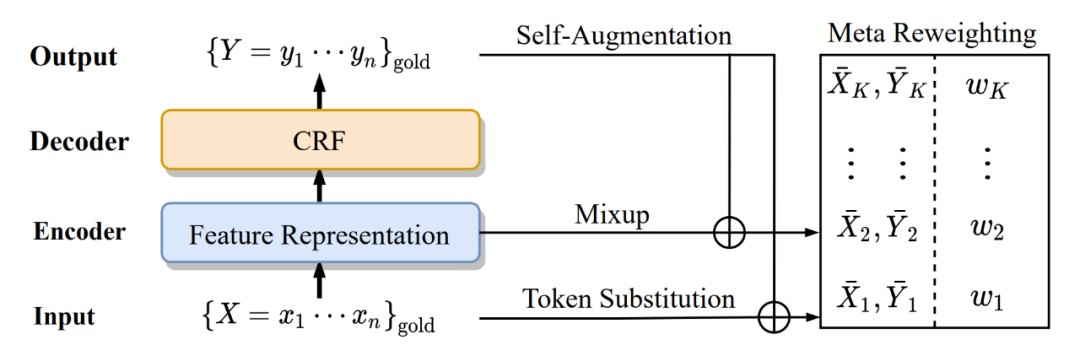
Method
2.1 Baseline
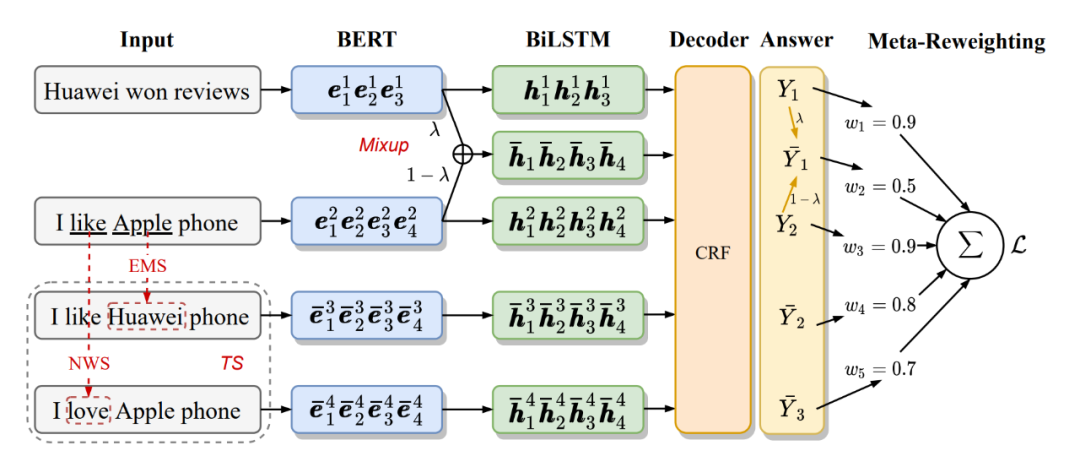
本文的 basic 模型使用 BERT+BiLSTM+CRF 进行 NER 任务。首先给定输入序列 ,使用预训练的 BERT 得到每个 token 的表征。
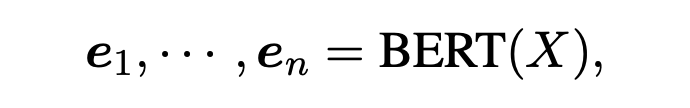
然后使用 BiLSTM 进一步抽取上下文的特征:
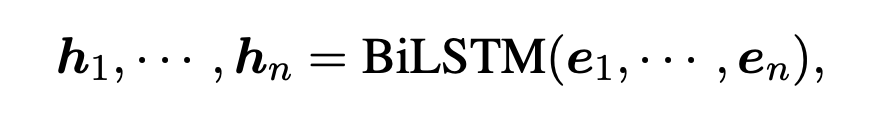
最后解码过程使用 CRF 进行解码,先将得到的表征过一层线性层作为初始的标签分数,定义一个标签转移矩阵 T 来建模标签之间的依赖关系。对于一个标签序列 ,其分数 计算如下:
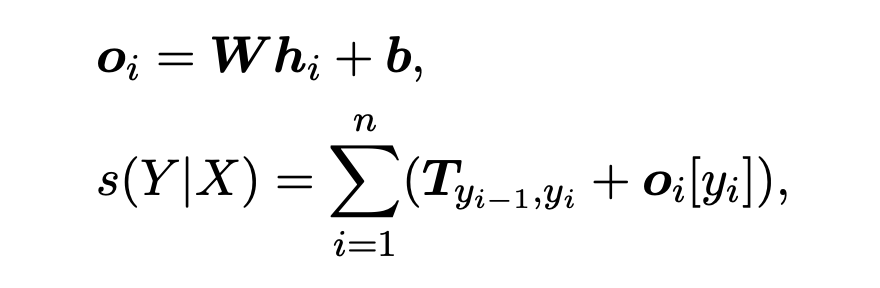
其中 W、b 和 T 是模型的参数,最后使用维特比算法得到最佳的标签序列。训练的损失函数采用句子级别的交叉熵损失,对于给定的监督样本对 (X, Y),其条件概率 P(Y|X) 计算如下:
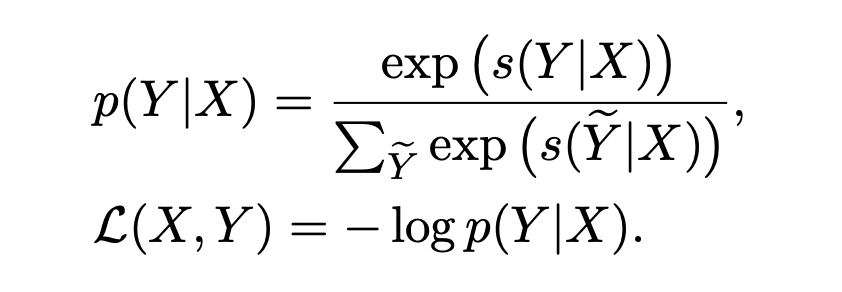
其中 为候选标签序列。
2.2 自增强方法
2.2.1 Token Substitution(TS)
token 替换是在原始的训练文本中对部分 token 进行替换得到伪样本。本文通过构建同义词词典来进行 token 替换,词典中既包含实体词也包含大量的普通词。遵循前人的设置,我们将所有属于同一实体类型的词当作同义词,并且添加到实体词典中,作者将其称为 entity mention substitution (EMS)。同时,我们也将 token 替换扩展到了“O”类型中,作者将其称为 normal word substitution (NWS)。作者使用 word2vec 的方法,在 wikidata 上通过余弦相似度找到 k 个最近邻的词作为“O”类型词的同义词。这里作者设置了参数 (此参数代表 EMS 的占比)来平衡 EMS 和 NWS 的比率,在 entity diversity 和 context diversity 之间达到更好的 trade-off。
2.2.2 Mixup for CRF
不同于 token 替换在原始文本上做增强,mixup 是在表征上进行处理,本文将 mixup 的方法扩展到了 CRF 层。形式上,给定一个样本对 和 ,首先用 BERT 得到其向量表示 和 。然后通过参数 将两个样本混合:
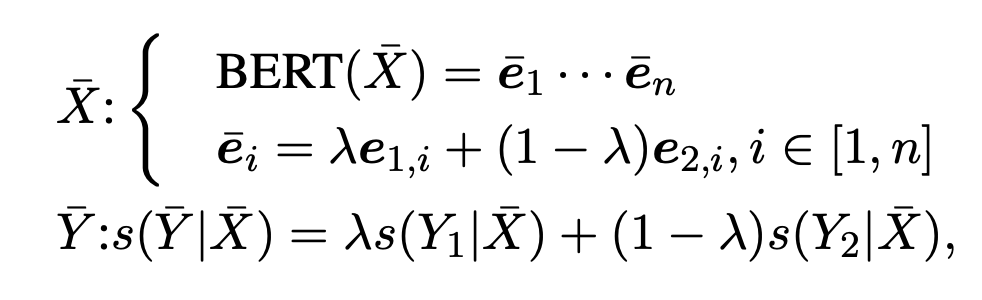
其中,n 为 , 从 分布中采样。损失函数变为:
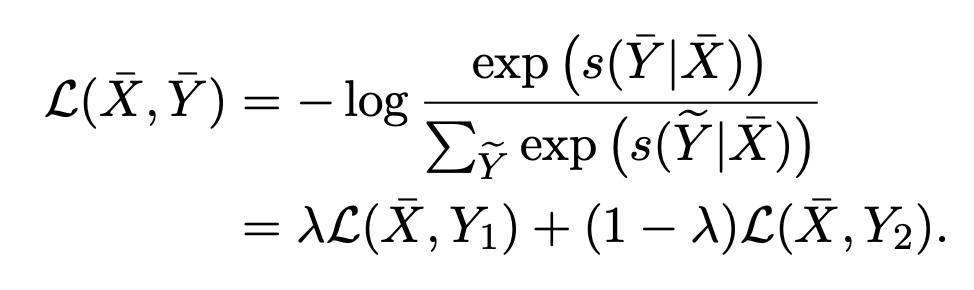
2.3 Meta Reweighting
有别于句子级的分类任务,NER 这类 token 级别的任务对于上下文高度敏感,一些低质量的增强数据会严重影响模型的效果。在本文中,作者使用 meta reweighting 策略为 mini batch 中的训练数据分配样本级的权重。
在少样本设置中,我们希望少量的标注样本能够引导增强样本进行模型参数更新。直觉上看,如果增强样本的数据分布和其梯度下降的方向与标注样本相似,说明模型能够从增强样本中学到更多有用的信息。
算法流程如下:

实验
3.1 实验设置
数据集采用 OntoNotes 4、OntoNotes 5、微博和 CoNLL03,所有数据集均采用 BIOES 标注方式。
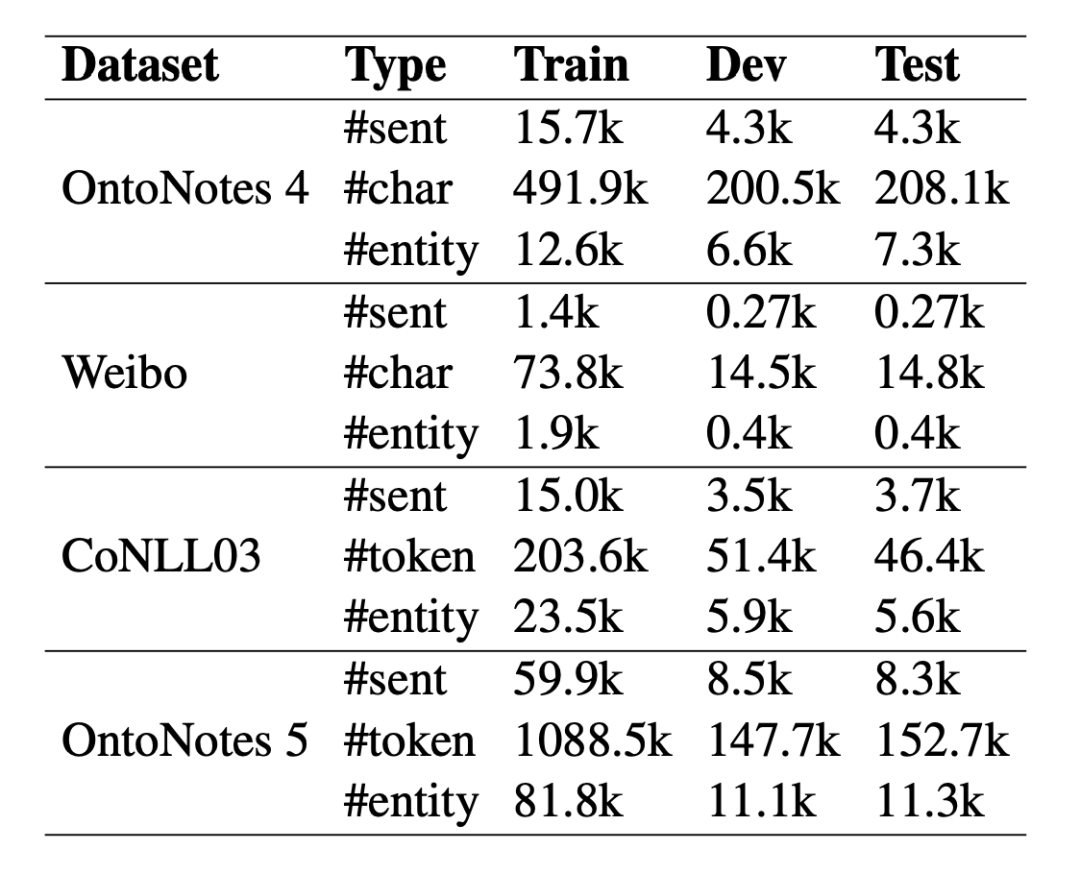
对于 NWS,使用在 wikipedia 上训练的 GloVe 获取词向量,取 top5 最近邻的词作为同义词, 取 0.2, 在 Beta (7, 7) 中进行采样,评价指标使用 F1 值。3.2 主实验本文在小样本设置和全监督设置下都做了实验,结果如下:
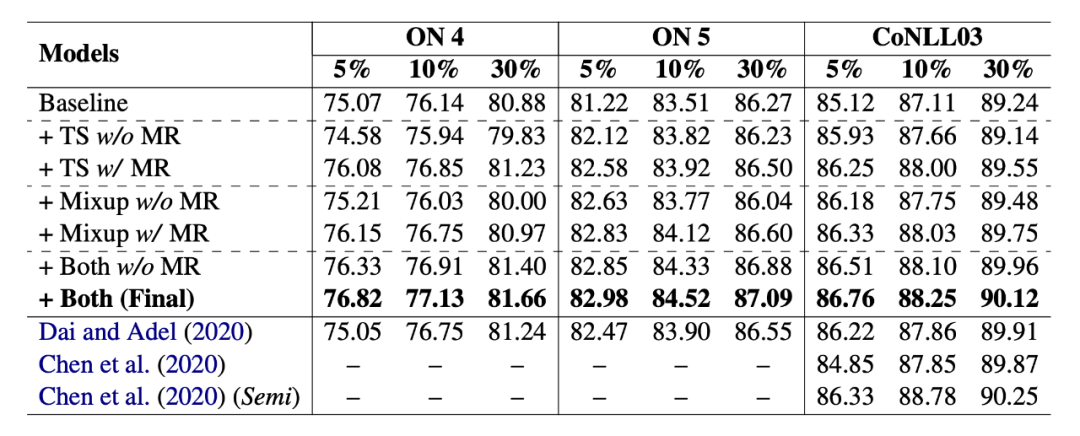
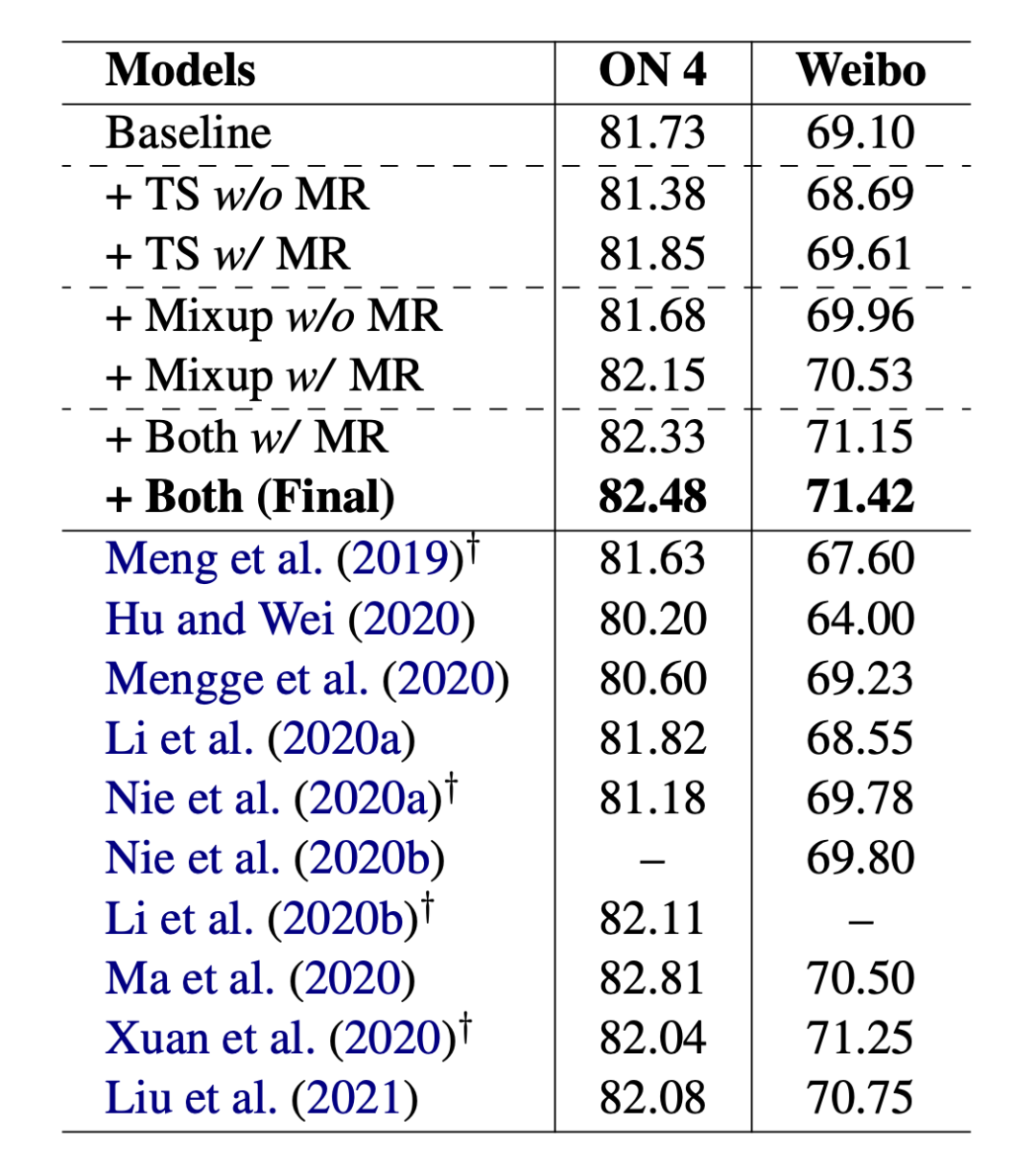
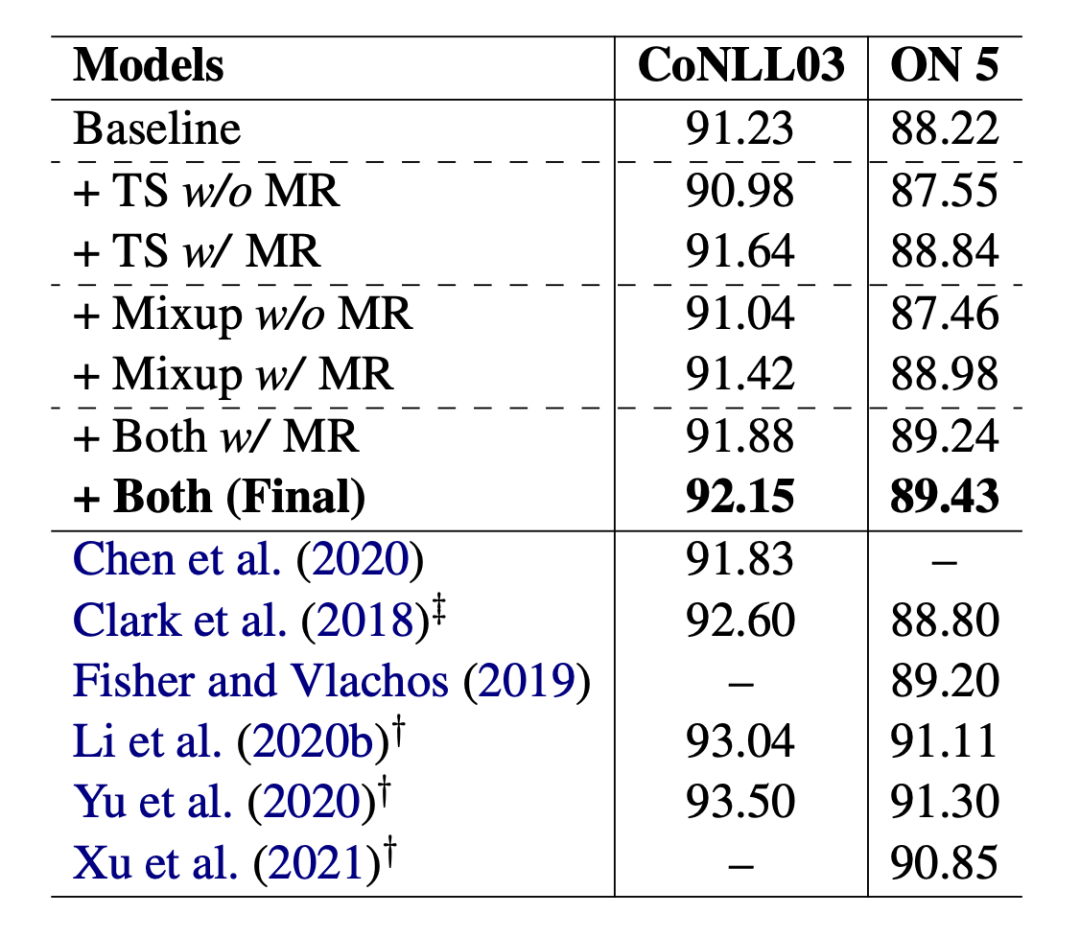
3.3 分析
作者首先在 CoNLL03 5% 设置下做了增强数据量对实验结果的影响:
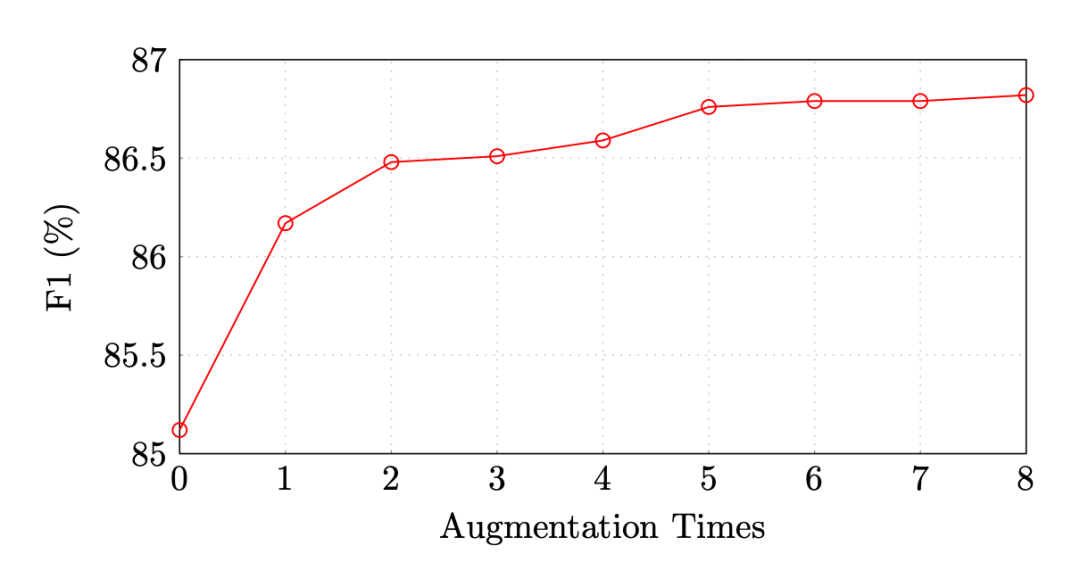
可以看出,在增强数据是原始训练数据的 5 倍之后,模型的效果就趋于平缓了,单纯的增加增强样本数并不能带来效果上持续的增长。
作者在三种小样本设置下对参数 的影响:
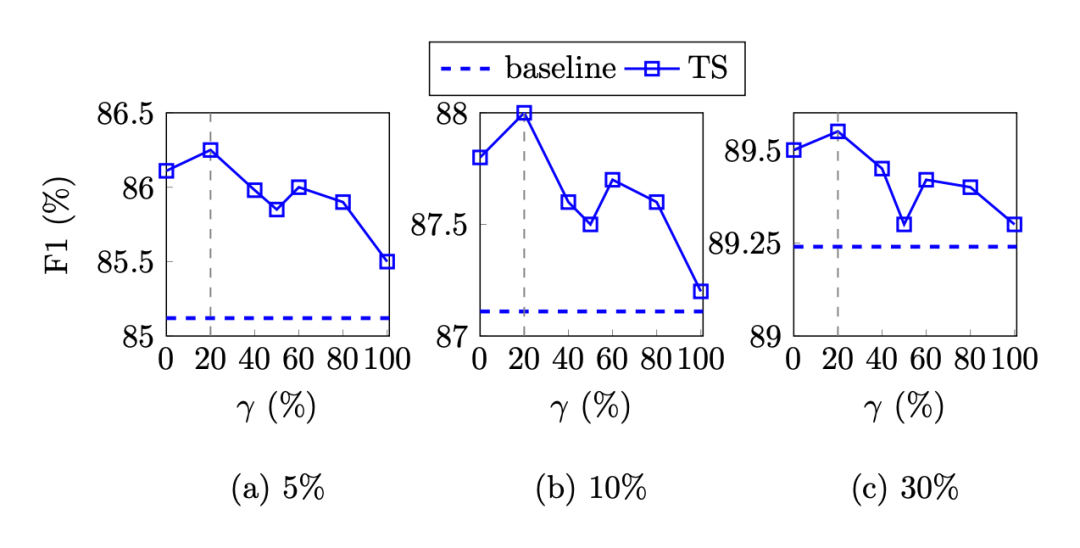
可以看出在 20% 时效果最好,而且相比之下,只使用 NWS 比只使用 EMS 效果更好。可能的一个原因是实体词在文本中是稀疏的,NWS 能够产生更多不同的伪样本。
接着作者分析了 mixup 参数 (Beta 分布参数 )的取值:
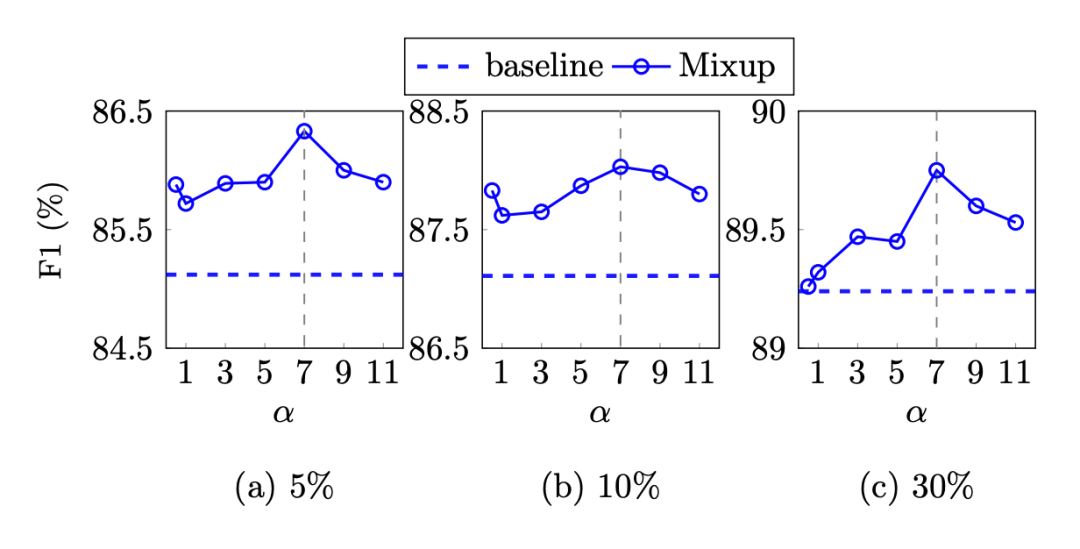
因为本文 Beta 分布的两个参数都取 ,其期望总是 0.5,当 增大时,分布的方差减小,采样更容易取到 0.5,实验结果表明当 取 7 时整体效果最好。最后作者还分析了 mixup 添加在不同位置的不同结果:
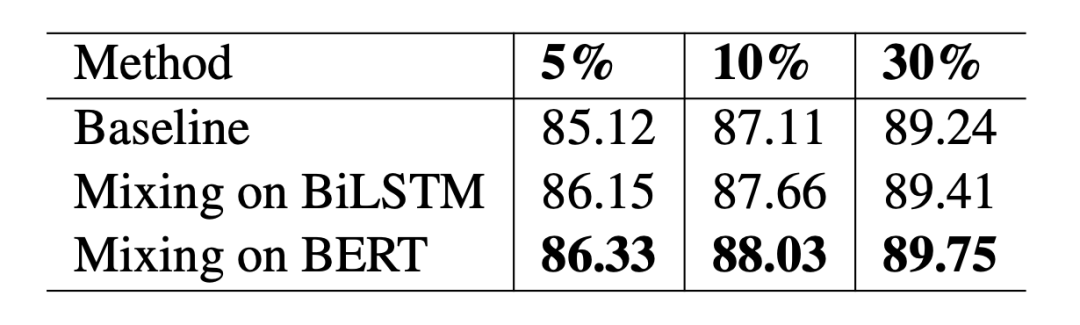
总结
本文提出了 meta reweighting 策略来增强伪样本的效果。是一篇很有启发性的文章,从梯度的角度出发,结合类似于 MAML 中 gradient by gradient 的思想,用标注样本来指导伪样本训练,为伪样本的损失加权,对伪样本的梯度下降的方向进行修正使其与标注样本更加相似。
-
基于支持样本的快速增强学习算法2010-01-22 596
-
采用伪卫星技术增强GPS定位系统来提高定位性能2010-07-23 670
-
大样本支持向量机分类策略研究_胡红宇2017-03-19 746
-
Meta与DassaultSystèmes携手为Solidworks3DCAD软件提供增强现实支持2018-02-08 1155
-
Bose推出了一款利用声音来实现增强现实效果的太阳眼镜2018-12-12 3738
-
研究人员们提出了PBA的方法来获取更为有效的数据增强策略2019-08-02 5621
-
一种基于伪标签半监督学习的小样本调制识别算法2022-02-10 838
-
基于k近邻与高斯噪声的虚拟困难样本增强方法2022-05-12 1153
-
一个联合的meta-reweighting的策略来自然的进行整合2022-08-03 389
-
yolov5和YOLOX正负样本分配策略2023-08-14 2310
-
Meta拒绝谷歌合作提议2024-03-06 717
-
高通与Meta合作优化Meta Llama 3,实现终端侧运行2024-04-22 473
-
Meta重组硬件部门Reality Labs,聚焦增强现实与元宇宙2024-06-20 693
-
Meta发布新AI模型Meta Motivo,旨在提升元宇宙体验2024-12-16 353
全部0条评论

快来发表一下你的评论吧 !

