

一种应用于5G eMBB场景下控制信道编码方案的优秀编码方式
今日头条
描述
在正式进入Polar码世界之前,我们先进行热身运动。
先看看对线性空间的定义,了解其中的基本概念。

这里,主要是对线性代数中的矩阵运算规律进行了总结。本质上,与我们学过的加法和乘法类似。
接下来,我们回到信息论中,了解关于编码的几个概念:

这里,我们需要知道二进制线性分组码的概念,K和N分别代表什么。定义中的GF(2)是指2元伽罗瓦域。伽罗瓦域,也称有限域,是仅含有限个元素的域,它是伽罗瓦(Galois,E.)于18世纪30年代研究代数方程根式求解问题时引出的。
首先,群论是法国天才少年数学家伽罗瓦发明的,它是信道编码的数学基础。
接下来,我们了解什么是校验矩阵,什么是内积。

你一定还记得上信息论课上,求生成矩阵G和校验矩阵H的生动画面吧。


极化码背景
在《Polar Code(一)概述》一文中,我们提到了离散无记忆信道。
离散信道:指的是输入符号集合和输出符号集合都是离散集合的信道。我们通常考虑离散信道的输入输出符号集合的元素是有限的。
信道无记忆:是指信道的任意两次传输是独立的,即信道对每个输入符号添加的噪声是独立的。
离散无记忆信道W可以用转移概率W(y/x)来描述,其中y∈Y是输出符号集合中的元素,x∈X是输入符号集合中的元素。W(y/x)表示在输入符号为x的条件下,输出符号是y的概率。其实,这与条件概率的概念类似,只是在信号处理领域,我们用转移概率来描述。
在给定信号源分布的情况下,即x∈X的离散分布律已知,整个传输系统(X,Y)的联合概率Pr(X=x,Y=y)=p(x)W(y/x)。
这里通俗一点讲,就是我们发送端的信源X是什么符号是已知的,经过信道H传输后,接收端收到了Y。
比如,你给朋友打电话,你的声音通过手机转化为电信号,再通过信号处理变为电磁波,通过手机内置的天线辐射出去。电磁波在自由空间中通过电场和磁场的交替转换,滚滚向前,通过基站检索你朋友所在的位置,把这个过程逆向,最终你朋友听到你的声音。
信号在传输过程中,不可避免会受到干扰和衰落,进而有可能影响传输质量。
我们回来再看看一个重要的公式,计算对数似然比:

一看就知道,还是在求概率。说好的编码,就是这样游走在线性代数、概率论和信息论之间。
LLR在Polar译码过程中将被使用,输入译码器的数据被称为软bit或者软值。
具体计算过程,这里就不展开了。有兴趣的朋友,继续深入研究。
下面,再学习几个定义。
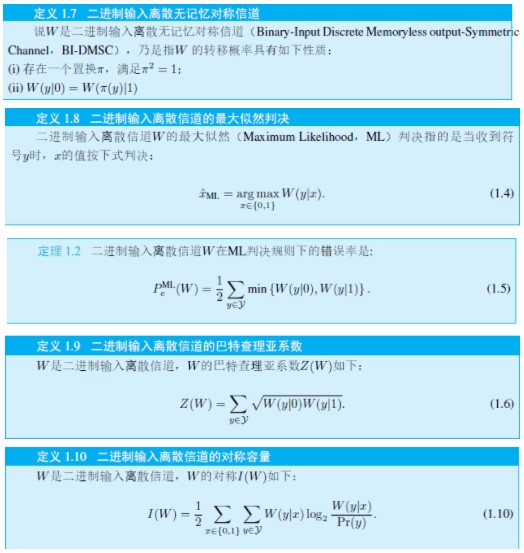
信道容量是信息论的内容,香农老爷子总是萦绕在我们身边。

继续我们的定义。

对于该文献中的部分推导是否严谨,有待考证。
下面,我们再看看关于二叉树的两个重要概念:二叉树攀升与坠落。
先看一幅图:
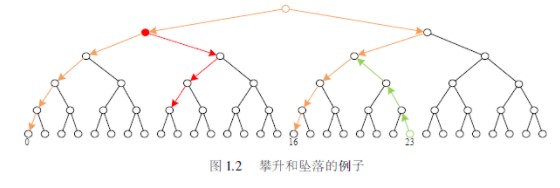
是不是想起了老子的经典名言:“道生一,一生二,二生三,三生万物”。
就是这样一颗树,在信息编码界树立了永远的丰碑。

从叶节点开始的攀升,对应的是标准SC译码器的比特值反馈计算过程。
从非叶节点出发的攀升,对应的是快速SC译码器的比特值反馈计算过程。


有点意思,编码和译码,玩的就是“0”,“1”。
审核编辑:刘清
- 相关推荐
- 信号处理
- 译码器
- 数字威廉希尔官方网站
-
信道编码问题2016-09-25 0
-
信道编码——引言2009-08-01 602
-
Turbo 码及交织技术在WCDMA 的信道编码方案中的应用2009-08-24 886
-
Turbo码及交织技术在WCDMA的信道编码方案中的应用2009-08-25 787
-
华为极化码胜选控制信道编码方案入选5G标准2016-11-19 1712
-
误读5G标准 华为距离5G还有多远?2016-11-21 1543
-
华为主推的Polar Code5G编码为何会引起业界轰动?2016-11-22 1248
-
5G只是和4G一样网速的提升?没你想的那么简单2016-11-26 7995
-
什么是信道编码?信道编码简史2018-05-14 28011
-
带你了解什么是信道编码2018-11-15 16392
-
5G NR的信道编码的关键技术和与4G的对比说明2019-10-18 2483
-
如何使用FPGA实现信道编码2020-08-18 1092
-
信道编码的发展历程介绍2021-02-23 5799
-
信道编码有哪几种 信道编码的作用及种类 信道编码的主要特点2023-06-28 6665
-
信道编码有哪几种 matlab的信道编码仿真2023-07-18 430
全部0条评论

快来发表一下你的评论吧 !

