

量子场论和真空神奇现象的解密
描述
在本文中,我会介绍一个非常令人惊奇的实验结果,它曾掀起了理论物理的新风暴。这个实验结果的名字叫做“兰姆位移”(Lamb shift),当时对氢能级的这一小小的深入探索,激发了以费曼、施温格和朝永振一郎等人为首的量子场论革命。我会向大家介绍兰姆位移是什么,以及解释这一现象发生当前的模型。弗里曼·戴森很好地总结了这一现象的重要性:
以兰姆位移为物理学中心讨论的那些年,是我们这代物理学家的黄金年代。人们都刚刚见证到这小小的位移,兰姆位移既难琢磨又难测量,我们对于粒子和场的思想正亟待更新。
与狄拉克氢原子模型不符的实验1940年代时的氢原子模型是狄拉克方程建立的,由一个质子和一个电子相互吸引的库仑势组成。狄拉克方程描述了宽泛的一类被称为费米子的粒子行为,电子也是其中的一种。物理学家们以为已经通过狄拉克方程对氢原子能级有了很好的理解——直到威利斯·兰姆的一个实验打破了一切。
1947年,兰姆-卢瑟福实验出现了一个异常结果——在和两个量子能级有着轻微的能量差异!这是怎么一回事呢?狄拉克方程预测这两个量子态的能量应该是一样的。
下面的图像展示了能量劈裂的性质。左边的能级分布是狄拉克方程所预测的,右边的则是实验中观察到的。左侧中间的那条线表示的是和两个能级,狄拉克方程预测两者的能量相同。然而,兰姆的实验发现这个能量发现这个能级分裂成了两个,像右图所示的那样,能级对应的能量更低,虽然差别很小。换句话说,这个现象是新的物理学内容。
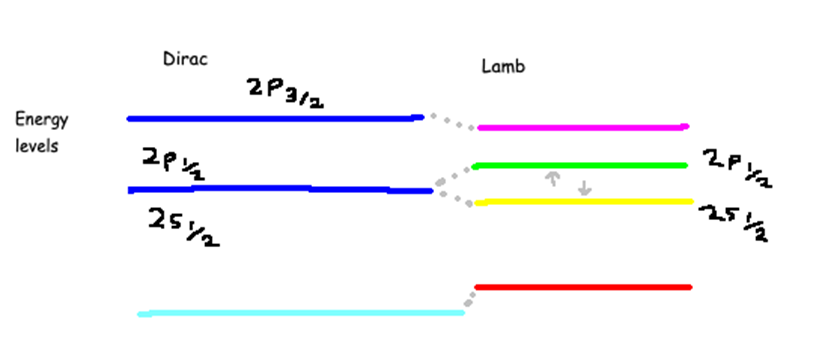
狄拉克模型预测的能级(左)和兰姆测量的能级(右)
兰姆测量出的能量差值在1028MHz左右,兰姆位移的发现让他赢得了1955年的诺贝尔物理学奖。
兰姆位移的解释——真空涨落兰姆位移显示出了狄拉克方程在精细的时候是不够完善的,细微的能级差暗示了物理学家还有一些内容必须补充。狄拉克方程这里没有考虑到的,是物理学家后来发现的真空涨落(vacuum fluctuation),是电子周围空间,或者说真空中可以测量的细微变化。
真空中的两个金属盘之间会存在一种神秘的现象,它们会有相互吸引力,叫做卡西米尔效应(Casimir effect),狄拉克时期这个力还不能被解释。由于真空中单独两个金属盘之间产生微小力的实验可以重复,这使得卡西米尔力变得既神秘、又无可争议。
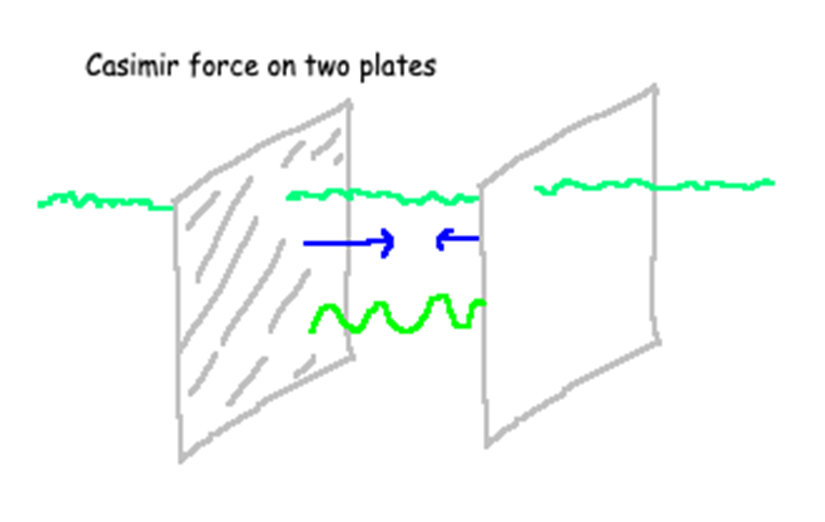
两金属盘之间的卡西米尔力
对于这个现象有着可能的解释模型。物理学家计算出真空中两个金属板之间可以储存连续变大的能量,甚至可以爆炸增长至无穷高的值。由于能量本身并不是一个可观测量,所以物理学家通过规范数学来认为,无穷高的能量可以从两板之间“泄露”出来。如果这样做会发现,有些量会凭空产生,其中之一便是卡西米尔力。由于这个力看上去像是从真空中凭空产生,因而我们通常把这个力认为是一种真空涨落。
当前对于真空涨落的理论是说微小粒子在其自身空间中不断地产生和湮灭,这个说法现在仍有争议。在之前,人们一直以为真空中不存在什么激动人心的事情。但卡西米尔效应打破了这一认知,现代量子场论认为真空本身就是高度活跃的,粒子和反粒子的产生导致了微量的能量变化。
为了深入理解这个问题,想象一下真空空间,在随机的一点产生了一个正粒子和反粒子,在产生的一瞬间它们又立刻碰撞湮灭了。这样微小的波动不断发生在真空当中,造成了实验观测的力在微小的量子水平的修正。
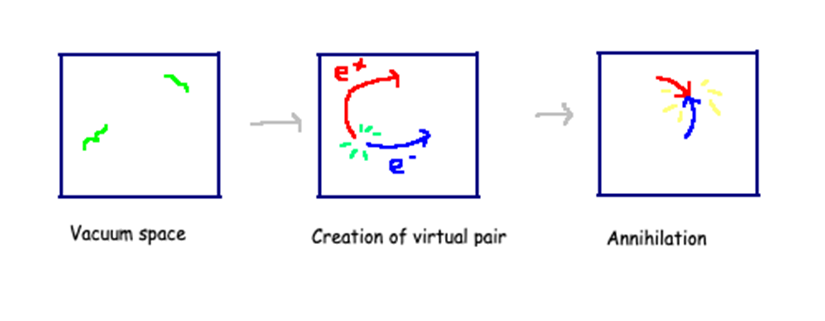
真空空间(左)、虚电子对的产生(中)和湮灭(右)
上面的图片展示了电磁场下发生的事件阶段,一个虚电子和其反粒子(也就是正电子),在一瞬间产生又湮灭。下面的动画就是在量子色动力学场背景下真空涨落的示意图。量子色动力学的理论一般用来描述夸克之间的联系。
Ahmed Neutron, CC BY-SA 4.0 via Wikimedia Commons
电子的真空涨落电子的情况是一样的,当电子被原子核内质子吸引,粒子会与电磁场发生相互作用。狄拉克很好地解释了这个的发生,但是却不能解释真空涨落略微改变相互作用的本质。
为了让解释更简单些,我们先考虑两个电子互斥的情形。我们该如何描述其中的相互作用呢?现在最可靠的电磁理论模型叫做“量子电动力学”(quantum electrodynamics),将力模拟为虚粒子的性质。这些虚粒子被叫做“虚光子”(virtual photon),当两个带电粒子之间产生电磁力时,它们之间会交换一个虚光子,从而产生运动。无论是粒子之间相互吸引还是排斥,都会进行光子交换。
为了计算和示意其中的作用,我们用费曼图来展示。
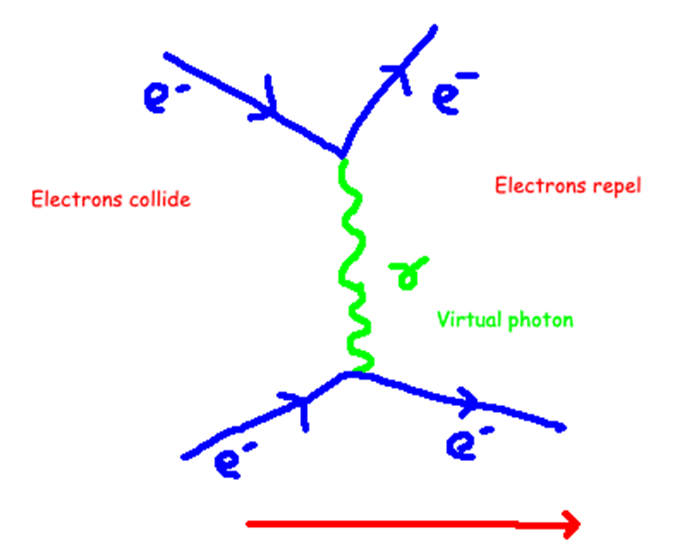
电子对碰撞(左红字)、交换虚光子(绿)以及排斥(右红字)的费曼图
从左至右来理解这张费曼图:左边有两个电子相互靠近,各带一个负电荷。交换虚光子的过程用绿色部分展示,这是产生排斥力的原因。于是两者像右侧所示那样向外散开。费曼图不仅仅是一个有用的工具,每张费曼图都可以清晰地展示物理学家计算作用强度和形态的一系列数学规则。
先不仔细考虑数学规则,这张费曼图表示的其实就是库仑力!
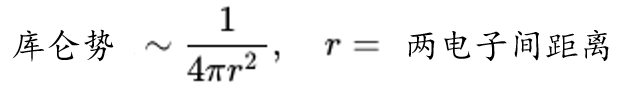
目前为止,这个模型还没有涉及真空涨落,只是重现了兰姆位移观测前的已知的结果。但兰姆位移则需要在上面的基础上再加一些图来解释。
我们怎么体现真空涨落?当时物理学家们意识到这个现象需要考虑到真空涨落。正如我之前提到的,涨落的形式以粒子和反粒子迅速产生湮灭为过程,它们必须成对存在来保证一些量(比如说电荷量)守恒。
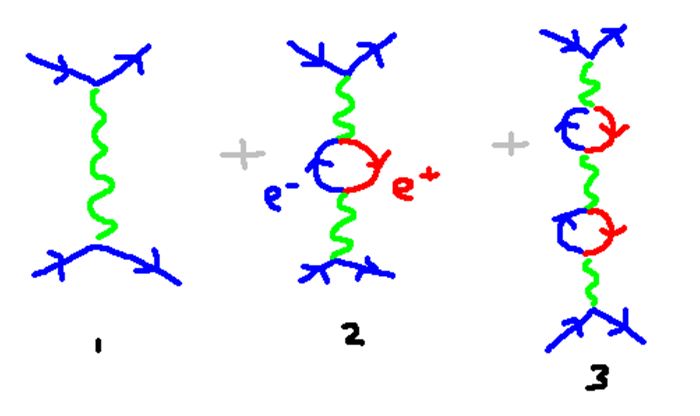
自然,我们需要添加些图来考虑这个过程。如上图所示,第一幅图基于已经考虑到的基本模型,接下来的两幅考虑了真空涨落。第二幅图中,交换光子的过程产生了一个电子-正电子对,又湮灭成一个光子,之后斥力产生;第三幅图中,光子产生电子-正电子对、湮灭成光子、产生另一对、然后再次湮灭!
重要的是,这个新的过程只会产生很小但是很关键的效应。比如说第二幅图是一个真空极化图,因为这个小波动很像磁铁的南北极。
这些图的准确描述需要经过大量的物理和数学培训,其中的任务艰巨而乏味。跳过这些数学计算,物理学家发现,修正后的势长得和库仑势非常相似,只是多了个小修正:

第二项这个修正项被称为Uehling项,通过微扰理论,可以推出和能级的确会劈裂成两条!拓展标准数学来包含这些真空效应的过程被称为重整化。
总结希望这篇文章给大家带来了一节量子场论和真空神奇现象的解密课程。
-
量子计算,未来已来2024-02-01 0
-
【量子计算机重构未来 | 阅读体验】+ 初识量子计算机2024-03-05 0
-
【量子计算机重构未来 | 阅读体验】+ 了解量子叠加原理2024-03-13 0
-
什么是“量子自旋霍尔效应”?2018-12-13 0
-
超导磁通量子计算机,超导磁通量子比特低频磁通噪声的测量 精选资料推荐2021-09-01 0
-
量子科学热潮背后隐藏的大骗局2017-12-08 31098
-
量子计算机到底有多神奇2018-02-05 4606
-
量子保密通信技术,引领韩国的5G时代2019-03-20 4788
-
量子通信和量子密钥分发的关系2020-06-19 6216
-
全景解密量子信息技术一文看懂2020-10-19 4414
-
量子电动力学的发展:费曼的诺贝尔奖2023-01-12 1006
-
科创筑梦 |“神奇量子”走进金寨县水竹坪实验学校2022-07-02 406
-
《图说本源产品》系列之四:量子芯片高真空存储箱2024-08-06 409
-
国光量子推出全球首个真空噪声芯片2024-09-24 569
全部0条评论

快来发表一下你的评论吧 !

