

射频威廉希尔官方网站 的5G NR调制技术解析
RF/无线
描述
近年来,随着移动通信技术的飞速发展,对数据传输速率要求越来越高,这就意味着需要设计更加完美的射频威廉希尔官方网站 才能满足更改的要求,也就等于需要不断提升射频技术,这样才有助于提高数据的传输速率。提高数据传输速率的方法有很多,今天我们就以5G NR调制为例来给大家分享一种实用的方法。
一种提高传输速率的思路是使用更高阶的QAM 调制方式,例如5G NR 的256QAM PDSCH,微波的1024QAM,2048QAM和4096QAM 调制。更高阶的QAM 调制方式对系统也提出了更高的要求。例如某个系统的EVM 测试结果为3%,这个EVM 算好还是不好,单纯从数值看似乎很好,但是EVM 的好坏与否不仅要看数值,还要看其调制阶数,不同调制阶数对EVM要求不同。直观来看,更高阶QAM 调制方式对EVM 有更高要求,但是具体要求是多少?例如对1024QAM 调制,EVM 要小于多少才能实现正常通信?本文主要讨论这个问题。EVM确定了,就可以指导系统信噪比SNR(SIGNAL NOISE RATIO)的指标分解和预算。
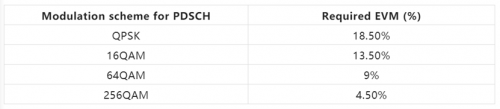
例如3GPP TS38.141对5G NR 不同调制方式的PDSCH EVM 要求如下表,从表中也可以看到随着调制阶数的提高,EVM 的要求在不断提高,这些EVM 是怎么定出来的?目前已经有客户开始测试1024QAM 的PDSCH,TS38.141 没有给出1024QAM 的EVM 要求,在测试的时候1024QAM EVM多少才算通过?本文将会给出答案。
表1、TS38.141对不同阶QAM EVM指标要求
1、QAM 调制及EVM 以及EVM 与SNR 的关系
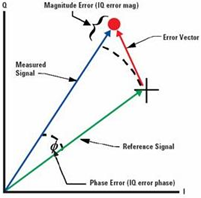
图1、EVM定义
QAM 调制信号通常用其EVM 来衡量信号质量,EVM是英文Error Vector Magnitude缩写,意为误差向量幅度,其定义为误差矢量Error Vector 的幅度与参考信号Reference Signal 幅度的比值,有时候用百分比比表示,有时候用dB 表示。通常测量的EVM为其RMS 值,计算公式如下:
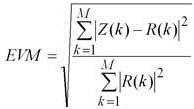
EVM 可以与信噪比SNR 相互换算,在星座图中,EVM 是以电压表示的,因而二者之间的换算公式如下,当然如果有编码增益,要在该公式中考虑编码增益,例如扩频增益。
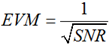
2、不同阶QAM 信号对EVM 的要求
不同阶QAM 对信号的抗干扰能力是不一样的,数字调制信号调制方式越复杂,频率带宽利用率越高,调制方式越复杂,抗干扰能力越差,功率利用率低,也就是说接收时需要较高的C/N比,才能达到相同传输质量,选择调制方式需要根据通信系统在这两个方面折衷256QAM 的符号点间距离比BPSK 调制近的多,这意味256QAM 和BPSK 相比容易被干扰而造成误码。
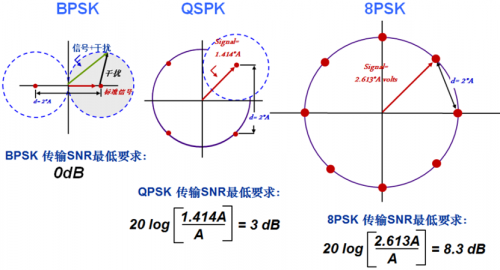
图2、不同调制方式抗干扰能力
从EVM 的含义看,结合几种调制方式的星座图拿来看,如果要保证通信正常,也就是星座点不发生误判,则要求每个星座点的误差矢量幅度最大为0.5a(其中a 为相邻星座点之间的间距),即|E|max<0.5a,因而每个星座点需要落在以参考信号为中心,半径为0.5a 的圆内。由于不同星座点的参考信号幅度是不一样的,离原点最远的那个星座点对应的参考信号幅度最大,记为|R|max,则其可容忍的EVM 最小,即EVM_thre=0.5a/|R|max,只要所有星座点的EVM小于EVM_thre,就不会发生误判,即总的EVM 小于EVM_thre。下图中的A=0.5a,表示相邻星座点间距的一半。
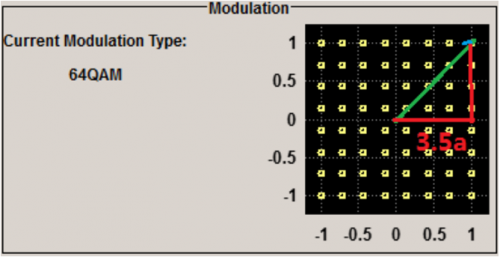
图3、64QAM EVM_thre 示意图
比如64QAM,星座图可以看作是间距为a 的8x8 阵列,那么距离原点最远的那个星座点坐标就是(3.5a,3.5a),矢量长度为1.414x3.5a,为了不发生误判,允许的矢量误差要小于半个星座间距(0.5a),这时的EVM<0.5a/(1.414x3.5a)=10.10%,为了保证接收机正常解调,留有一定的余量,5G NR 协议TS38.141 将64QAM 的EVM 限值设定在9%,是合理的。
当然这种估算方法保证了所有星座点的都不会发生误判,由于距离原点近一点的星座点参考信号幅度会小些,其EVM 会大些也不会发生误判,假设所有星座点同时达到最大误差矢量|E|max=0.5a,同时所有星座点等概率出现,此时系统的EVM 达到容忍上限,EVM 再大就会误判。此时系统的EVM RMS 值成为EVMRMS_thre,只要EVM 小于改值EVMRMS_thre,则系统一定不会发生误判。

图4、计算不同QAM 调制方式下对系统EVM 和SNR 要求门限
通过图4 Matlab 代码就可以计算出EVMRMS_thre 和EVM_thre,并计算出了其对系统SNR 的要求值。不同调制方式下对系统要求的EVM 和SNR 门限如表2 所示。从表中可看出,调制阶数越高,对系统的EVM 和SNR 要求就越高。
表2、不同QAM 调制方式对系统EVM 和SNR 要求
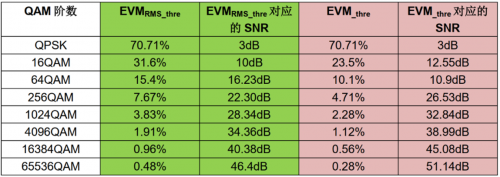
以目前已经使用的最高调制阶数4096QAM 为例,其对系统的EVM 的RMS值要求小于1.91%,如果以最远点计算EVM 要求小于1.12%。如果将信号源和频谱仪直接相连,相当于在没有衰落的静态信道条件下,EVM RMS 值最好一般在0.2%左右,所以4096QAM 对EVM 的要求已经接近于硬件的极限水平。
3、实验验证
使用信号源产生一个4096QAM 信号,使用频谱分析仪进行解调。
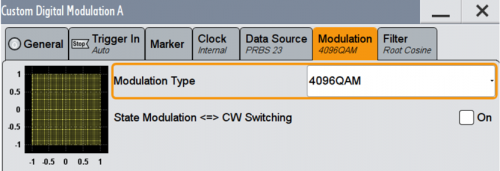
图5、生成4096QAM 调制信号
在不额外增加噪声的条件下,FSW 的解调结果如图6,其EVM 很好,星座图清晰可见。
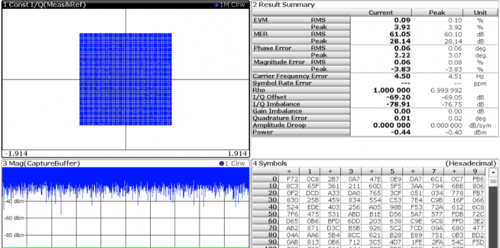
图6、不加噪声下FSW 对4096QAM 信号解调结果
根据表1 计算结果,4096QAM 对系统的EVM 要求必须小于1.91%,对应的SNR 为34.36dB。在上述信号基础上增加-34dB 的AWGN 噪声,此时加噪声后信号的解调结果如图8 所示,星座图已经接近于模糊和误判,对应的EVM 测试结果为1.56%,与理论计算1.91%还是比较接近。
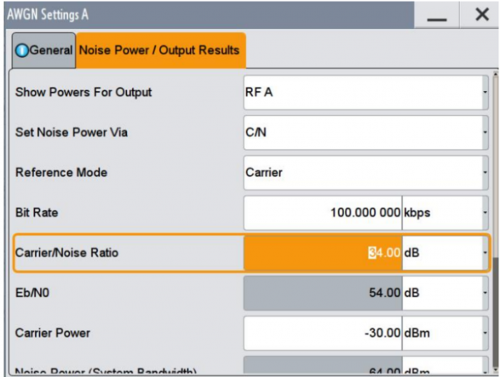
图7、4096QAM 信号增加-34dB 的AWGN 噪声
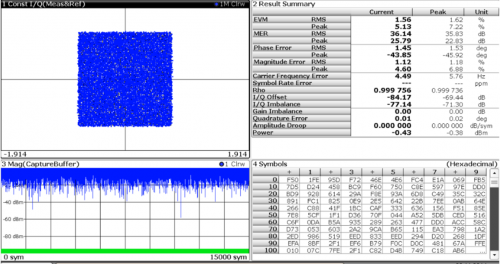
图8、加-34dB 噪声下FSW 对4096QAM 信号解调结果
4、结论
更高阶的QAM 调制方式对系统EVM 和SNR 提出了更高的要求,系统的EVM 测试结果算好还是不好,不能只单纯看EVM 数值,还要看其调制阶数。本文计算了不同调制阶数下星座点不发生误判时对系统的EVM 和SNR 要求,具体结果参考表2,该结论可以理解调制阶数与EVM的关系以及对系统SNR的要求,可以用来指导系统设计和器件选型。
编辑:黄飞
-
什么是5G NR?2017-05-03 0
-
详解5G NR标准 有哪些创新性的新技术2018-01-29 0
-
5G调制解调芯片哪家强?华为上榜2018-10-25 0
-
GaN功率放大器在5G应用中的可能性?2019-03-14 0
-
定义了首个5G NR规范的无线技术盘点2019-06-18 0
-
什么是5G天线及射频?2019-09-17 0
-
哪些无线技术定义了首个5G NR规范呢?2021-01-01 0
-
5G射频测试技术白皮书解析2021-01-13 0
-
5G NR信号的解调分析2023-05-06 0
-
5G NR RRC协议之NR系统消息解析2023-05-06 0
-
5G NR RRC协议解析—SIB12023-05-06 0
-
5G NR RRC协议解析_测量配置measConfig2023-05-10 0
-
剑指百亿中速率物联网连接 高通推出全球首个5G NR-Light调制解调器和射频方案2023-02-09 1591
-
高通推出全球首个5G NR-Light调制解调器及射频系统,赋能新一轮5G终端扩展2023-02-10 779
全部0条评论

快来发表一下你的评论吧 !

