

一种基于空间相关性分数域的探地雷达回波信号增强方法
电子说
描述
针对探地雷达回波中去除直达波和噪声干扰而削弱目标信号的问题,提出了一种基于空间相关性分数域的探地雷达回波信号增强方法,利用目标信号在临近测点之间的关联性,采用KL变换获得相关性特征值,根据相关性大的特征值重构目标图像,再将处理后的图像变换到分数域,通过分数阶傅里叶变换抑制直达波与噪声,最终得到目标回波增强的探地雷达图像。实验结果验证了所提方法的有效性。
0 引言
探地雷达因其良好的穿透性与高分辨率被广泛应用于路面地基等无损探测中。但公路地基等地下环境比较复杂,如铺设碎石等对探地雷达发射电磁波的随机散射、地基含水区导致的部分电磁波被吸收能量降低、直达波影响等,使得接收回波噪声干扰较大,而目标能量较弱,给地下无损探测的目标识别带来了困难。
在噪声干扰的抑制方面,减平均法常用来去除探地雷达数据中的不变成分,如地面直达波、天线间耦合波、地下其他分层界面的回波等。文献是采用基于背景矩阵相减的方法抑制直达波和地面反射回波。文献[2]是采用K-Means方法快速自动滤除了B-scan图像中的强直达波。但是对于随机离散的非目标体回波、多个双曲线交叉部分回波等干扰,采用类似减平均法是无效的。文献采用自适应阈值函数滤波的方法去除了空洞信号的随机噪声,但是对于有效信号增强的效果并不明显。文献采用KL变换有效增强了地震信号。
为了进一步去除探地雷达无损探测中的直达波并增强目标回波信号,本文结合KL变换与分数域分析,对采集原始回波图像进行KL变换,提取目标特征参数,重构出目标信号增强的图像,再通过分数域转换,获得适合目标凸显而直达波被抑制的处理图像,有利于目标信号识别与提取。
1 探地雷达回波信号理论
1.1 电磁波传播基本原理
探地雷达发射高频电磁波来探测地下低损耗的介质材料,其理论基础是电磁波基本理论,而麦克斯韦方程组是研究电磁波传播的基础,其麦克斯韦方程组表达式如下:
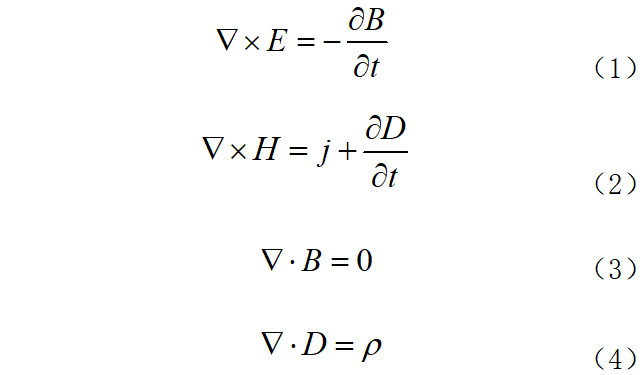
式中:E表示电场强度;B表示磁感应强度;H表示磁场强度;D表示电位移;j表示电流密度;ρ表示电荷密度。 而电磁场与探测介质之间存在着场量本构关系,本构关系本质上是介质内的分子或原子在电场作用下产生的极化现象。在均匀、线性且各向同性的介质中,其本构关系可以表示为:
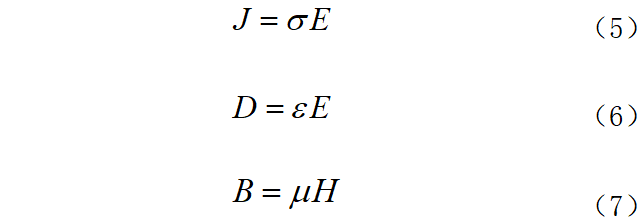
式中:σ表示电导率;ε表示介电常数;μ表示磁导率。
1.2 探地雷达测量方式
探地雷达采集的数据根据测试点的数目不同可以分为A-scan与B-scan测量方式,对于天线位置处的每一个测点,采集的回波信号称为一个A-scan,当天线沿着固定的方向移动形成多次测量,而一个测量形成一个A-scan,此时采集的数据包含有多个A-scan,称为B-scan。
探地雷达采用高频电磁波进行地下探测,常用的测量方式有反射测量、折射测量和透射测量。浅层测量中普遍采用反射测量方式,而剖面法为常用的反射测量方法。通过剖面法反射测量可以获得比较好的横向分辨率,也能通过合理的天线移动反演出地下波速等信息。
剖面法的测量结果以B-scan方式呈现,测点的位置在图像横坐标中体现,而纵坐标记录了每一个测点数据的回波双程时间。在实际应用中,常采用收发同置天线,即发射天线与接收天线在同一测点发射电磁波、接收回波。图1为收发同置天线情况下剖面法示意图。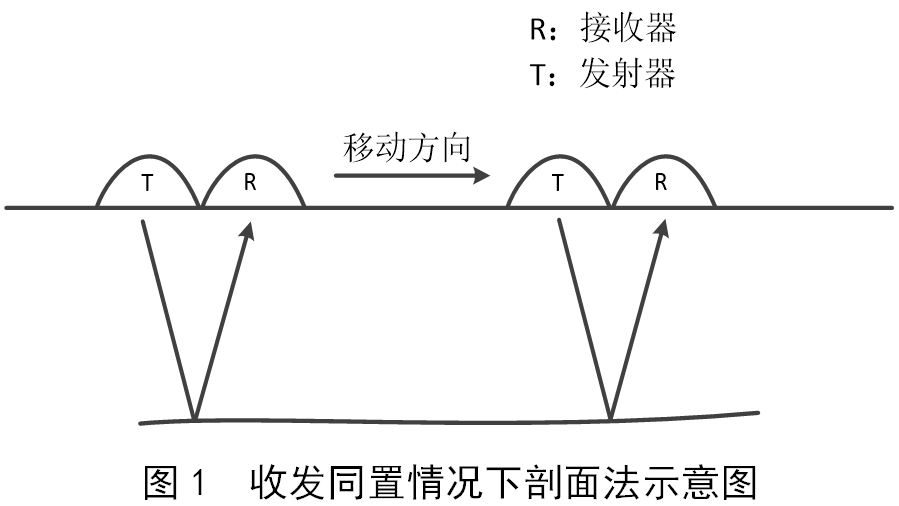
2 空间相关性分数域分析
2.1 基于KL变换的目标回波空间相关性分析
由于地下目标所处的环境复杂,尤其是不均匀的介电环境容易产生大量杂波与干扰,会不同程度地抑制目标信号,单一的减平均处理方法很难将其彻底去除。但考虑到电磁波经过地质环境、经过小尺寸颗粒干扰与经过目标体会产生不同频率与相位特征,这些特征会随着不同的尺度空间获得不同的呈现效果;并且地下环境中干扰呈现随机性,而目标在回波数据的临近采样点处呈现相关性,因此可以采用KL变换方法进行目标回波空间相关性分析。
KL变换是最小均方误差意义下的最优正交变换。KL变换的主要特性是一个信号经过KL变换后,其各个分量之间互不相关,能去除不相关信号;若信号之间是相关的,那么通过KL变换能提取相关信号,同时消除时间维度上的干扰噪声。在探地雷达的目标回波数据中,经KL变换后目标回波的相关性由其协方差矩阵的特征值度量。
设接收的B-scan回波数据可以表示为矩阵X,数据采集中有N个测点,每个测点采集了M个数据,即可以表示为:
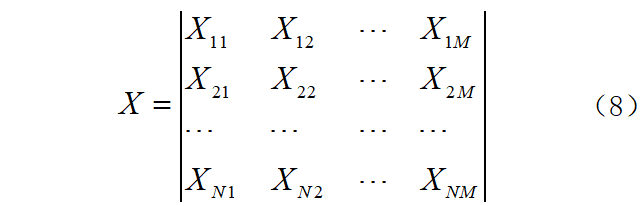
式中:Xij表示每个测点i采集到的第j个数据。 将X进行线性变换,得到Y=LTX,其中L为变换矩阵,令A为协方差矩阵对角阵,那么得到:
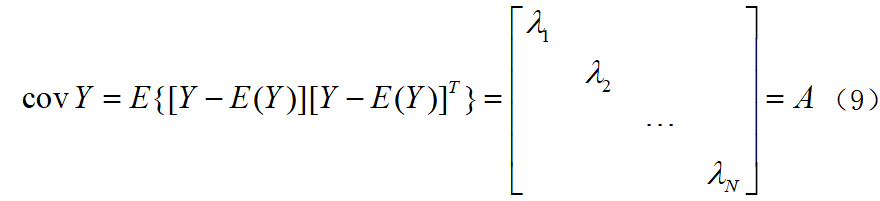
式中:E(·)表示统计平均;A的对角分量λi是特征值。 考虑到covX是对称正定矩阵,那么必定存在正交阵L=(L1L2…LN),使得:
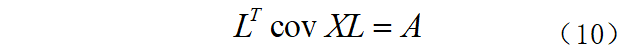
Li为N维矢量,令Li是对应于特征值λi的归一化非零特征向量,则有:
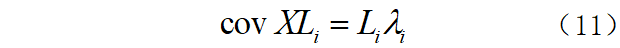
因此对X作正交变换可以得到:
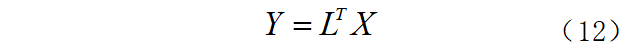
即Y为X的KL变换。 考虑到目标回波在一定测点范围内具有较强的相关性,因此使得矩阵X的部分行与列也具备较强的相关性,可以利用KL变换提取相关性特征信号,从而去除杂波与干扰。上述特征值表征了相关性强弱,特征值大的成分重建的信号相关性强,特征值小的成分重建的信号相关性弱,因此对特征值λi按照从大到小顺序排列:λ1≥λ2≥…≥λN,若取前k个主分量Y’=(y1,y2,…yk,0,…0)T,那么重构出的图像信号可以表示为:
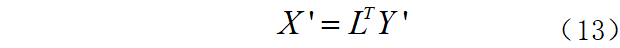
从图2中可以看出,原始探地雷达图片中含有大量噪声与干扰信息,在B-scan图像中呈现出噪点,而在埋地目标的双曲线两侧信号已经被噪点湮没,并且因为噪声的存在,图中深处的情况并不明晰。
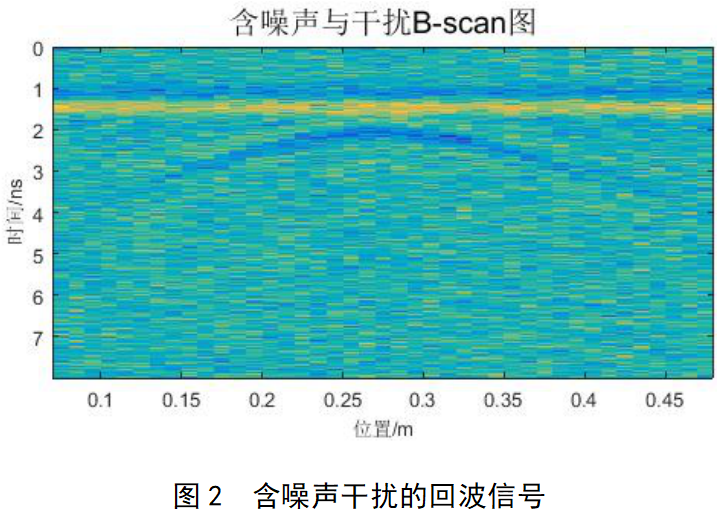
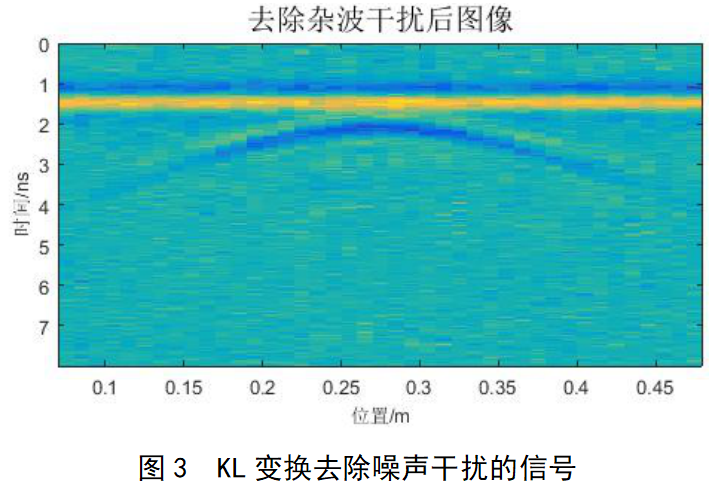
由于地下噪声源是随机的,而目标在0.15~0.4 m位置之间的测量数据是关联的,因此使用上述KL变换方法,能较好地去除图中噪点,还原目标信息,如图3所示。此外,在去除了噪声干扰后,目标信息有一定程度的增强。
2.2 分数域目标信号增强方法分析
分数域的表现形式为分数阶傅里叶变换,分数域是0~1之间的域空间,即以观看时频面的角度去旋转时频面的坐标轴,然后再从观察频域的角度去分析信息。
二维信号x(t,s)的分数阶傅里叶变换的定义为:
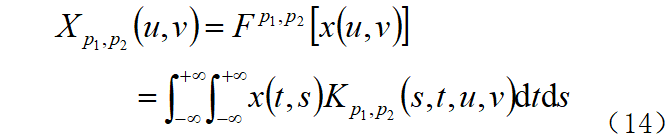
其中,
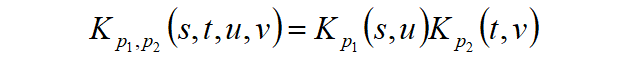
是可分离的变换核函数。 采用分数域进行图像信号分析,可以理解为将图像信号在时频空间绕着原点旋转ɑ角度,其中α=piπ/2,pi为阶数,i为信号维度,当pi=0时,即没有变换的时域图像信号;当pi=1时,即传统傅里叶变换的频域图信号。
3 实验结果与分析
本实验采用真实沙坑场景模拟地下目标检测环境,沙坑的长为1.2 m,宽为1.8 m,高为0.6 m。实验中首先测量沙坑中10处不同位置沙的相对介电常数,取平均相对介电常数值为4.25,在沙表面下方0.2 m深处埋入一空矿泉水瓶,水瓶以水平于沙表面的方式放置,且水瓶的直径为0.08 m,长为0.2 m。使用的探地雷达为美国GSSI公司SIR-20系列,雷达天线的中心频率为400 MHz。
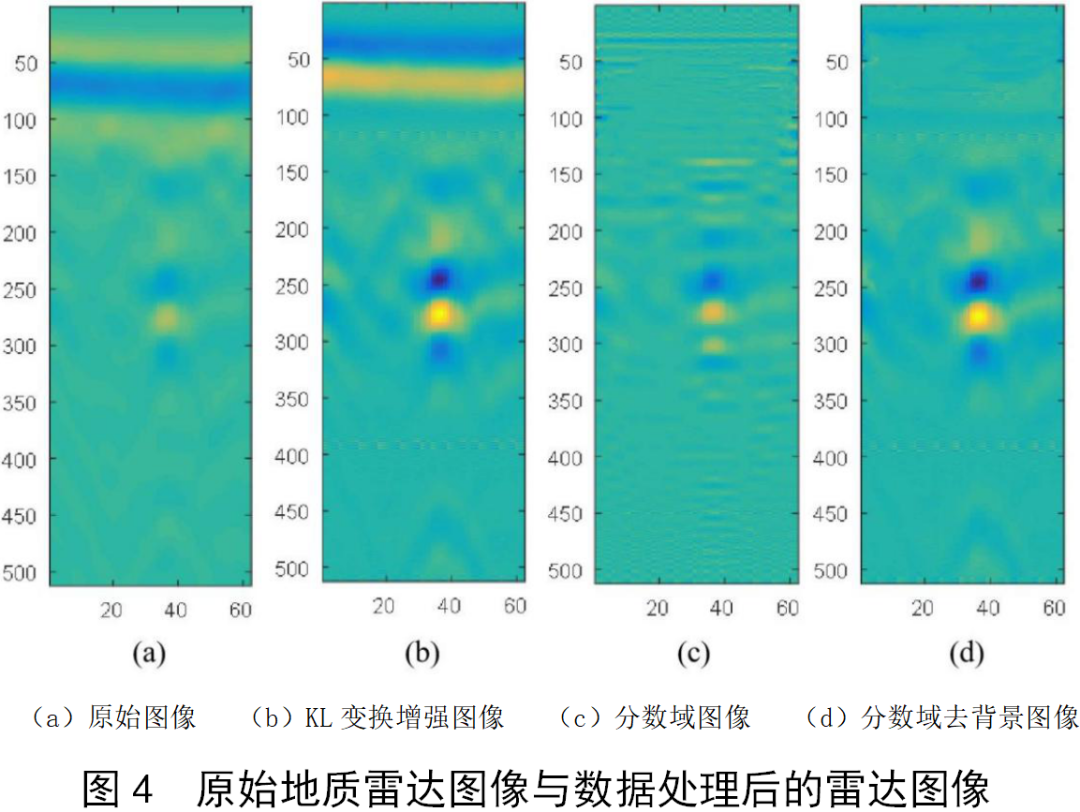
在以上实验场景中,测得的空矿泉水瓶原始图像如图4(a)所示,原始图像中存在地面直达波,在图像纵向40~120间隔内,并贯穿整个横轴;而在横轴约40,纵轴200~300间隔内存在目标回波;整幅图像受到沙坑内壁的影响存在一些干扰信号,由于直达波占据了较大能量,目标信号的雷达回波比较弱。对图4(a)做KL变换,得到图4(b),可以看出经过KL变换后,目标区域的能量明显增强,但同时也增强了部分直达波信号,需要注意的是,在KL变换中,将纵轴约100处的直达波旁瓣当作干扰信号滤除了,使得直达波原来的旁瓣与主峰值信号极性反向,形成了以黄色能量为峰值的主导信号。再对增强后的图像进行分数阶傅里叶变换,这里取p1=0.12,p2=0.37,得到的分数域图像如图4(c)所示,经过此参数下的变换,能滤除直线状的直达波。最后经过分数域逆变换,得到如图4(d)所示的图像空间信号,此时还原的图像为去除了直达波且增强了目标信号的图像,有利于目标的识别与检测。

4 结语
探地雷达无损探测中采集的回波信号通常包含了能量较强的直达波信号,同时伴随有地质环境产生的噪声干扰信号,这些信号使得目标回波信号较弱,不易被识别。本文通过对回波图像进行KL变换,提取表征相关性目标特征信息的特征值,通过拟KL变换得到增强后的图像,再根据分数阶傅里叶变换将图像变换到分数域,从而去除直线状的直达波干扰,保留目标信息。
审核编辑:刘清
-
无人机+探地雷达=地雷探测器?2018-10-22 0
-
一种自主产生式的雷达回波模拟器中频部分的设计论述2019-07-19 0
-
如何利用FPGA构建一种通用的雷达回波信号实时模拟系统?2021-04-29 0
-
浅地层探地雷达回波倒相的自适应处理2009-03-04 1274
-
一种雷达回波信号模拟器的设计与实现2009-05-08 660
-
改进的奇异点检测算法在探地雷达信号检测中的应用2009-06-26 479
-
多站数据采集在探地雷达中的应用2009-08-19 583
-
随机相位编码抑制步进频率探地雷达RFI的研究2009-11-13 855
-
基于DSP的探地雷达图像液晶显示技术2010-03-30 531
-
探地雷达回波信号数据采集的设计2011-01-05 1019
-
HHT方法在探地雷达回波信号特征提取上的应用2012-07-06 1163
-
探地雷达可防止道路坍塌发生2018-08-14 4461
-
探地雷达方法与应用PDF版电子书免费下载2019-02-27 2170
-
浅析探地雷达的四大测量方式2020-12-26 2993
-
满足探地雷达主机应用需求的高速板对板连接器2023-09-06 605
全部0条评论

快来发表一下你的评论吧 !

