复杂模型的分网技术划分比较

网格划分是进行有限元分析和计算的前提，也是最费时间最费精力的一项前处理技术，网格划分的质量对有限元计算的精度和计算效率都有着最为直接的影响，对于大变形的情况甚至影响到解的收敛性。目前比较通用的分网软件主要有Hypermesh、ANSA、ANSYS、MARC等，本文就复杂模型的分网技术进行简明的阐述。

自由网格划分

自由网格划分是自动化程度最高的网格划分技术之一，它在面上（平面、曲面）可以自动生成三角形或四边形网格，在体上自动生成四面体网格。通常情况下，可利用Hypermesh的2D面板的automesh来对面和网格单元自动划分。

对于复杂几何模型而言，自动分网方法省时省力，但缺点是单元数量甚至会出现单元不能达到预想的效果，如在某些地方需要较少单元，而在另外的地方需要更多的单元时，通常不容易控制。因此需要对面进行一些几何分块处理，以得到符合分网工作者的意愿的具有较高计算效率的网格。

对于三维复杂模型只能生成四面体单元，分网效率极高，只要设置相关参数就等得到较好的网格，但是网格数量取决于几何模型的最小特征，网格数量通常非常大，因此为了获得更高的计算效率的有限元网格，通常要对几何模型进行一些处理，和二维情况类似，可以进行分块处理，如进行局部细分。

映射网格划分

映射网格划分是对规整模型的一种规整网格划分方法，其原始概念是：对于面，只能是四边形面，网格划分数需在对边上保持一致，形成的单元全部为四边形；对于体，只能是六面体，对应线和面的网格划分数保持一致；形成的单元全部为六面体。

目前大多数分网软件对这些条件有了很大的放宽，包括：

面可以是三角形、四边形、或其它任意多边形。

面上对边的网格划分数可以不同，但有一些限制条件。

面上可以形成全三角形的映射网格。

体可以是四面体、五面体、六面体或其它任意多面体。

体上对应线和面的网格划分数可以不同，但有一些限制条件。

对于三维复杂几何模型而言，通常的做法是利用线面切割功能，将其切割成一系列四、五或六面体，然后对这些切割好的体进行映射网格划分。当然，这种纯粹的映射划分方式比较烦琐，需要的时间和精力较多，但能保证较高的网格质量。

拖拉、扫略网格划分

对于由面经过拖拉、旋转、偏移等方式生成的复杂三维实体而言，可先在原始面上生成壳单元形式的面网格，然后在生成体的同时自动形成三维实体网格。对于已经形成好了的三维复杂实体，如果其在某个方向上的拓扑形式始终保持一致，则可用扫略网格划分功能来划分网格；这两种方式形成的单元几乎都是六面体单元。

在Hypermesh三维面板中的solidmap功能，可以实现几种形式的拖拉和扫略，如从单元到面，从面到面，可以选择的拉伸方式也多种，根据具体的情况进行灵活选择，通常，采用扫略方式形成网格是一种非常好的方式，对于复杂几何实体，经过一些简单的切分处理，就可以自动形成规整的六面体网格，它比映射网格划分方式具有更大的优势和灵活性，一般情况下，要把复杂的几何模型划分成完全的六面体单元，通过几何处理来分块，再用扫略功能是最主要的划分方法。

在ANSA下，情况也类似，ANSA是很具优势的基于几何的分网软件，其建面功能十分强大，在没有体这一概念的情况下，可以实现模型的分块，操作简单但效率很高，是未来分网软件发展的大趋势

混合网格划分

混合网格划分即在几何模型上，根据各部位的特点，分别采用自由、映射、扫略等多种网格划分方式，以形成综合效果尽量好的有限元模型。混合网格划分方式要在计算精度、计算时间、建模工作量等方面进行综合考虑。

通常，为了提高计算精度和减少计算时间，应首先考虑对适合于扫略和映射网格划分的区域先划分六面体网格，应尽量通过切分等多种布尔运算手段来创建合适的区域（尤其是对所关心的区域或部位）；其次，对实在无法再切分而必须用四面体自由网格划分的区域，采用带中节点的六面体单元进行自由分网。

自由度耦合和约束方程

对于某些形式的复杂几何模型，可以利用ANSYS的约束方程和自由度耦合功能（Abaqus中的tie功能）来促成划分出优良的网格并降低计算规模。

比如，将相邻的体在进行独立的网格划分（通常是采用映射或扫略方式）后再“粘结”起来，由于各个体之间在几何上没有联系，因此不用费劲地考虑相互之间网格的影响，所以可以自由地采用多种手段划分出良好的网格，而体之间的网格“粘结”是通过形函数差值来进行自由度耦合的，因此连接位置处的位移连续性可以得到绝对保证，如果非常关注连接处的应力，可以如下面所述再在该局部位置建立子区模型予以分析。

子模型等其它手段

子模型是一种先总体、后局部的分析技术（也称为切割边界条件方法），对于只关心局部区域准确结果的复杂几何模型，可采用此手段，以尽量小的工作量来获得想要的结果。

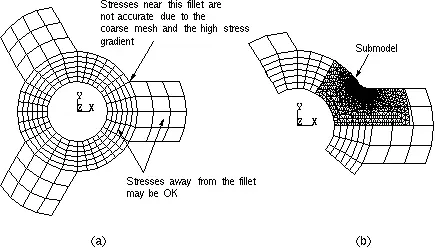
其过程是：先建立总体分析模型，并忽略模型中的一系列细小的特征，如导角、开孔、开槽等（因为根据圣维南原理，模型的局部细小改动并不特别影响模型总的分析结果），同时在该大模型上划分较粗的网格（计算和建模的工作量都很小），施加载荷并完成分析。其次，（在与总体模型相同的坐标系下）建立局部模型，此时将前面忽略的细小特征加上，并划分精细网格（模型的切割边界应离关心的区域尽量远），进行求解计算。

该方法的另外好处是：可以在小模型的基础上优化（或任意改变）所关心的细小特征，如改变圆角半径、缝的宽度等；总体模型和局部模型可以采用不同的单元类型，比如，总体模型采用板壳单元，局部模型采用实体单元等。

巧妙地利用结构的对称性对实际工作大有好处，一是可以大大减少计算规模，二是可以便于施加准确的边界条件，航空发动机涡轮盘的计算就是典型的例子。对于常规的结构和载荷都是轴对称、循环对称、平面对称的问题，首先应利用其对称性。

总之，对于复杂几何模型，综合运用多种手段建立起高质量、高计算效率的有限元模型就进行数值计算的最开始最关键的步骤，本文仅仅涉及到一些大的方向，实际问题涉及面广，如网格过度与拓扑结构等相关处理都是网格划分技术中经常遇到的问题，用户只有在实际工作中不断摸索、总结和验证才能最终对复杂模型网格划分计算掌握透彻，灵活运用。