为什么数学家研究纽结？

纽结理论（knot theory）已经超越了抽象的数学好奇心，推动了数学及其他领域的许多发现。

纽结理论最初是为了理解宇宙的基本构成。1867年，当科学家们急切地试图找出可以解释所有不同种类物质的方法时，苏格兰数学家和物理学家彼得·格思里·泰特（Peter Guthrie Tait）向他的朋友和同胞威廉·汤姆森爵士（Sir William Thomson）展示了他用于产生烟圈的设备。汤姆森——后来成为开尔文勋爵（与热力学温标同名）——被环迷人的形状、稳定性和相互作用所吸引。他的灵感将他引向了一个令人惊讶的方向：也许，他想，就像烟圈是空气中的漩涡一样，原子是发光以太中结成纽结的涡旋环，物理学家曾认为，光通过以太这种无形介质传播。  

虽然这个维多利亚时代的想法现在听起来可能很荒谬，但这并不是一个轻率的研究。这个漩涡理论有很多值得借鉴的地方：纽结的多样性，每个纽结略有不同，似乎反映了许多化学元素的不同性质。涡旋环的稳定性也可能提供原子所需的持久性。  

涡旋理论在科学界获得了关注，并激发了泰特开始将所有纽结制成表格，创造了他希望等同于元素周期表的东西。当然，原子不是纽结，也没有以太。到1880年代后期，汤姆森逐渐放弃了他的涡旋理论，但那时泰特被他的纽结的数学优雅所吸引，他继续他的制表项目。在这个过程中，他建立了纽结理论的数学领域。  

我们都熟悉纽结——它们让我们的脚能穿上鞋，让船固定在码头上，让登山者能从下面的岩石上来。但这些纽结并不完全是数学家（包括泰特）所说的纽结。虽然缠绕起来的线团可能看起来打了结，但总是可以解开它。要打一个数学纽结，你必须将线的自由末端插在一起以形成一个闭环。  

因为纽结像绳子（或译为弦）一样灵活，数学家将纽结理论视为拓扑学的一个子领域，即对可延展形状的研究。有时可以解开一个纽结，让它变成一个简单的圆，我们称之为“（可）解纽结”（unknot）。但更多时候，解开一个纽结是不可能的。  

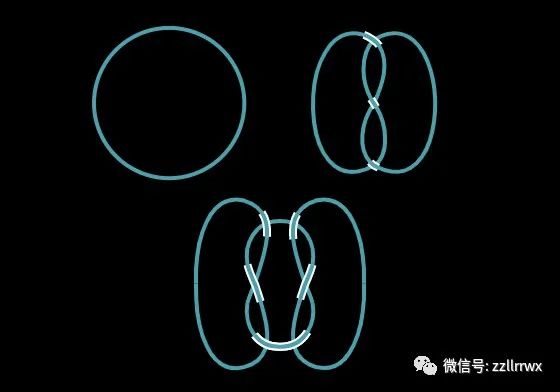
三个简单的纽结（从左上角顺时针方向）：（可）解纽结、三叶纽结（trefoil）和方形纽结。  

纽结也可以组合形成新的纽结。例如，将称为三叶草的简单纽结与其镜像结合会产生一个方形纽结。（如果你加入两个相同的三叶纽结，你就得到一个奶奶纽结（granny knot）。

   

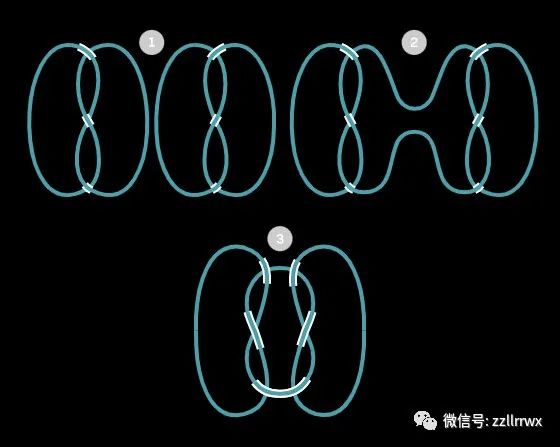
将三叶纽结及其镜像连接起来，形成一个方形纽结。   使用数字世界的术语，数学家说三叶纽结是素纽结，方纽结是（复合、合成）合纽结，（可）解纽结既不是素的，也不是合的（就与数字1一样，既不是素数，也不是合数）。这个类比在1949年得到了进一步的支持，当时霍斯特·舒伯特（Horst Schubert）证明了每个纽结要么是素纽结，要么可以唯一地分解为素纽结。  

创建新纽结的另一种方法是将两个或多个纽结交织在一起，形成一个链。波罗密欧环（Borromean ring）之所以如此命名，是因为它们出现在意大利Borromeo波罗密欧家族的徽章上，它就是一个简单的例子。  

 

为了形成Borromean环，三个环必须相互连接，而没有两个单独的圆环相连。  

汤姆森和泰特并不是第一个以数学方式看待纽结的人。早在1794年，卡尔·弗里德里希·高斯（Carl Friedrich Gauss）就在他的个人笔记本上写下并画了纽结的例子。高斯的学生约翰·利斯廷（Johann Listing）在他1847年的专著《拓扑学的初步研究》（Vorstudien zur Topologie）中写到了纽结——这也是拓扑学一词的起源。

但泰特是第一个研究纽结理论基本问题的学者：所有可能的纽结的分类和制表。通过多年的艰苦工作，仅使用他的几何直觉，他就发现并对所有素纽结进行了分类，当投影到平面上时，最多有七个交叉点。

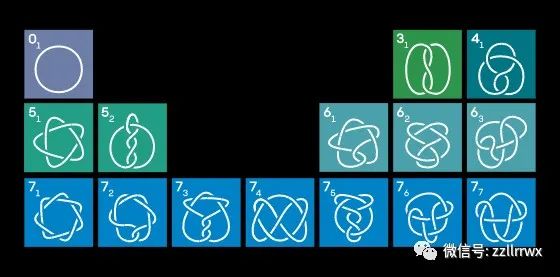
以元素周期表的样式排列的可解纽结和所有具有七个或更少交叉（忽略镜像）的素纽结。

在19世纪末，泰特得知另外两个人——托马斯·柯克曼牧师（Rev. Thomas Kirkman）和美国数学家查尔斯·利特尔（Charles Little）——也在研究这个问题。在他们的共同努力下，他们将所有素纽结分类为多达 10 个交叉点，其中许多具有 11 个交叉点。令人惊讶的是，他们10个及10个以内交叉点的纽结表是完整的：没有错过任何纽结。

值得注意的是，泰特、柯克曼和利特尔在没有后来几年中发现的定理和技术的情况下取得了如此多的成就。但对他们有利的一件事是，大多数小纽结都是“交替的”，这意味着它们有一个投影，其中交叉点表现出一致的上-下-上-下模式。

交替纽结具有比非交替纽结更容易分类的特性。例如，很难找到任何纽结投影的最小交叉数。但是泰特多年来错误地认为所有的纽结都是交替的，他推测了一种判断是否找到最小数字的方法：如果一个交替投影没有可以通过翻转部分纽结即可消除的交叉点，那么它一定是交叉次数最少的投影。

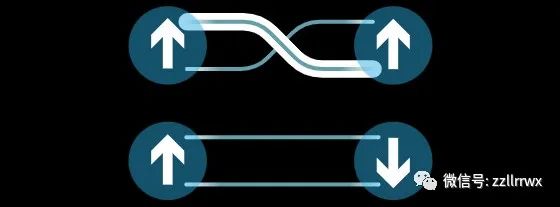
特称任何可以通过翻转部分纽结来消除的交叉点都是“无价值的”（nugatory）或无关紧要的。

泰特关于交替纽结的另外两个猜想最终都是真的。然而，这些著名的猜想直到1980年代末和90年代初，使用沃恩·琼斯（Vaughan Jones）于1984年开发的数学工具后，才被证明。琼斯因在纽结理论方面的工作而获得菲尔兹奖。

不幸的是，交替的纽结只能带你走这么远。一旦我们进入有八个或更多交叉的纽结，非交替纽结的数量就会迅速增加，这使得泰特的技术变得不那么有用。

这个8-交叉纽结，作为真爱之人的纽结，不能用交替的投影来绘制。

所有 10-交叉纽结的原始表是完整的，但泰特、柯克曼和利特尔重复计算了。直到1970年代，曾在普林斯顿大学研究纽结理论的律师肯尼斯·佩尔科（Kenneth Perko）才注意到其中两个纽结是彼此的镜像。为了纪念他，他们现在被称为Perko对（Perko pair）。

这两个 10-交叉纽结，称为 Perko 对，是同一个纽结。

在过去的一个世纪里，数学家们发现了许多聪明的方法来确定纽结是否真的不同。从本质上讲，这个想法是识别一个不变量——与节点相关的属性、数量或代数实体，通常可以简单地计算。（这些属性具有可着色性（colorability）、桥数（bridge number）或 翻滚（writhe） 等名称。有了这些标签，数学家现在可以很容易地比较两个纽结：如果它们在任何给定的属性上不同，那么它们就不是同一个纽结。然而，这些性质都不是数学家所说的完全不变量，这意味着两个不同的节点可能具有相同的性质。

由于所有这些复杂性，纽结的制表仍在进行中也就不足为奇了。最近，在 2020 年，本杰明·伯顿（Benjamin Burton）将所有多达 19 个交叉的素纽结进行了分类（有近 3 亿个） https://drops.dagstuhl.de/opus/volltexte/2020/12183/ 。

传统的纽结理论只在三维空间才有意义：在二维中，只有可解纽结是可能的，而在四维中，额外的空间允许纽结自行解开，所以每个纽结都与可解纽结相同。

然而，在四维空间中，我们可以给球面打结。为了理解这意味着什么，想象一下以规则的间隔切割一个普通的球面。这样做会产生圆圈，就像纬度线一样。然而，如果我们有一个额外的维度，我们可以把球面打结，所以这些切片，现在是三维的，而不是二维的，可以成为纽结。

当我们在三维空间中切一个球面时，我们得到的是圆。但是在四维空间中打结的球面的切片可能是纽结。

这个想法是纽结理论最近最大的结果之一。2018年，当时的研究生丽莎·皮奇里洛（Lisa Piccirillo）解决了50年前的问题，即约翰·康威（John Conway）首次发现的11-交叉纽结。这个问题与一种叫做sliceness（可切性）的属性有关。正如我们所看到的，当我们在四维中切开一个打纽结的球面时，我们会在三维空间中获得一个纽结或链。有时我们可以从一个漂亮的光滑纽结球面中获得给定的纽结，但对于其他纽结，球面必须像一张废纸一样打结和皱缩。从本质上讲，Piccirillo证明了康威的纽结属于后一种类型。用技术术语来说，她证明了它不是“光滑切片”（smoothly slice）。

Lisa Piccirillo证明，康威纽结并不“光滑”。

几个世纪以来，纽结理论在数学领域纵横交错。它最初是数学的一个应用领域，汤姆森试图用纽结来理解物质的构成。随着这个想法的消失，它变成了纯数学的一个领域，是拓扑学这个有趣且仍然不实用的领域的一个分支。但近年来，纽结理论再次成为数学的一个应用领域，因为科学家利用纽结理论的思想来研究流体力学、电动力学、纽结分子如DNA等。幸运的是，当科学家们忙于研究其他事情时，数学家们正在建立纽结目录和解开它们秘密的工具。

审核编辑：刘清