KNN算法、分类回归树、随机森林的优缺点及应用实例

原理

KNN属于一种监督学习的分类算法，用于训练的数据集是完全正确且已分好类的。

如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN算法的指导思想是“近朱者赤，近墨者黑”，由邻居来推断出类别。

「计算步骤如下：」

算距离：给定测试对象，计算它与训练集中的每个对象的距离。包括闵可夫斯基距离、欧氏距离、绝对距离、切比雪夫距离、夹角余弦距离；

找邻居：圈定距离最近的k个训练对象，作为测试对象的近邻；

做分类：根据这k个近邻归属的主要类别，来对测试对象分类

「K的含义」：来了一个样本x，要给它分类，即求出它的y，就从数据集中，在x附近找离它最近的K个数据点，这K个数据点，类别c占的个数最多，就把x的label设为c。K-近邻法中的邻近个数，即K的确定，是该方法的关键。

「优点：」

简单，易于理解，易于实现，无需估计参数，无需训练；

特别适合于多分类问题（对象具有多个类别标签）。

「缺点：」

主要的不足：当样本不平衡时，如一个类的 样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本，某一类的样本数量很大，那么或者这类样本并不接近目标样本，或者这类样本很靠近目标样本。

计算量较大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。

可理解性差，无法给出像决策树那样的规则。

R 进行 KNN 的实例

 

 

# 简单示范，以iris数据集为例
train <- iris[sample(nrow(iris), 145),] # 训练数据
test <- iris[sample(nrow(iris), 5),] # 测试数据
head(test)
library(class)
aa <- knn(train = train[,1:4], test = test[,1:4], 
          cl = train[,5], k = 5)
aa
table(test[,5], aa)

 

 

输出结果：

 

 

> head(test)
    Sepal.Length Sepal.Width Petal.Length Petal.Width   Species
117          6.5         3.0          5.5         1.8 virginica
135          6.1         2.6          5.6         1.4 virginica
44           5.0         3.5          1.6         0.6    setosa
18           5.1         3.5          1.4         0.3    setosa
43           4.4         3.2          1.3         0.2    setosa
> table(test[,5], aa)
            aa
             setosa versicolor virginica
  setosa          3          0         0
  versicolor      0          0         0
  virginica       0          0         2

 

 

「随机数据进行KNN分类：」

 

 

# data
set.seed(12345)
x1 <- runif(60,-1,1)
x2 <- runif(60,-1,1)  
y <- sample(c(0,1),size=60,replace=TRUE,prob=c(0.3,0.7))   
Data <- data.frame(Fx1=x1,Fx2=x2,Fy=y)  
SampleId <- sample(x=1:60,size=18)  
DataTest <- Data[SampleId,]   # 测试集
DataTrain <- Data[-SampleId,]  # 训练集

par(mfrow=c(2,2),mar=c(4,6,4,4))
plot(Data[,1:2],pch=Data[,3]+1,cex=0.8,xlab="x1",ylab="x2",main="全部样本")
plot(DataTrain[,1:2],pch=DataTrain[,3]+1,cex=0.8,xlab="x1",ylab="x2",main="训练样本和测试样本")
points(DataTest[,1:2],pch=DataTest[,3]+16,col=2,cex=0.8)

# KNN 分类
library(class)
# 循环计算不同K时的错误率
## 测试集与训练集均为Data时，会出现过拟合，错误率会很低
errRatio <- vector()  # 全部观测的错判率向量
for(i in 1:30){
  KnnFit=knn(train=Data[,1:2],test=Data[,1:2],cl=Data[,3],k=i)
  CT=table(Data[,3],KnnFit)  # 计算混淆矩阵
  errRatio=c(errRatio,(1-sum(diag(CT))/sum(CT))*100)  # 计算错判率（百分比）
}
plot(errRatio,type="l",xlab="邻近个数K",ylab="错判率(%)",main="ErrorRatio",ylim=c(0,80))
# 训练集与测试集单独分开
errRatio1 <- vector()   # 测试样本错判率向量（旁置法）
for(i in 1:30){
 KnnFit=knn(train=DataTrain[,1:2],test=DataTest[,1:2],cl=DataTrain[,3],k=i) 
 CT=table(DataTest[,3],KnnFit) 
 errRatio1=c(errRatio1,(1-sum(diag(CT))/sum(CT))*100)    
}
lines(1:30,errRatio1,lty=2,col=2)  # 随着样本数增加，错误率趋于稳定

# 使用另一个函数 knn.cv()，在不指定测试集的情况下默认使用训练集
# 该函数使用留一法交叉验证方法，与 knn 有区别，适用于样本量少的情况
errRatio2<-vector()   # 留一法错判率向量
for(i in 1:30){   
 KnnFit<-knn.cv(train=Data[,1:2],cl=Data[,3],k=i) 
 CT<-table(Data[,3],KnnFit)  
 errRatio2<-c(errRatio2,(1-sum(diag(CT))/sum(CT))*100)     
}
lines(1:30,errRatio2,col=2)

# KNN 回归
set.seed(12345)
x1 <- runif(60,-1,1) 
x2 <- runif(60,-1,1) 
y <- runif(60,10,20)   
Data <- data.frame(Fx1=x1,Fx2=x2,Fy=y)
SampleId <- sample(x=1:60,size=18)  
DataTest <- Data[SampleId,]  
DataTrain <- Data[-SampleId,]  
mseVector <- vector()    
for(i in 1:30){
 KnnFit<-knn(train=DataTrain[,1:2],test=DataTest[,1:2],cl=DataTrain[,3],k=i,prob=FALSE) 
 # 回归结果为因子向量，需转换成数值型向量
 KnnFit<-as.double(as.vector(KnnFit))   
 mse<-sum((DataTest[,3]-KnnFit)^2)/length(DataTest[,3])   
 mseVector<-c(mseVector,mse)
}
plot(mseVector,type="l",xlab="近邻个数 K",ylab="均方误差",main="近邻数K与均方误差",ylim=c(0,80))

 

 

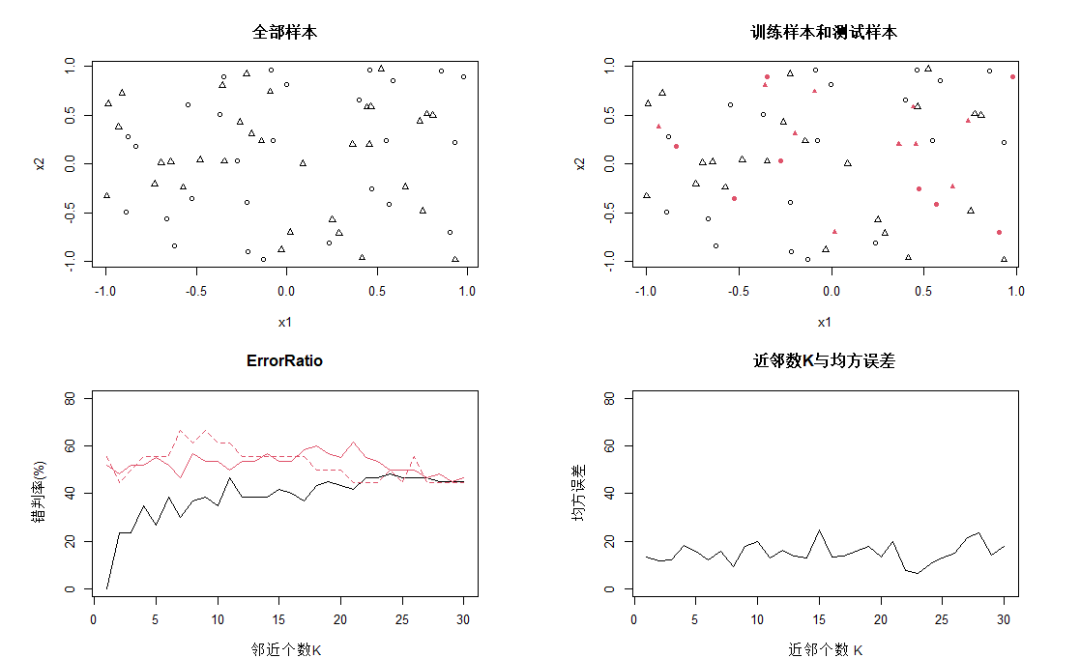
上图中，第一幅图为观测全体在特征空间中的分布，三角和圈分别表示输出变量的类别值分别为0和1；第二幅图是训练样本集和测试样本集的观测分布，其中有填充色的点属于测试样本集；

第三幅图黑线为全部观测进入训练样本集时的错判概率线，K=1时预测错误率一般为0；红色虚线为旁置法的错判概率曲线，K=9时达到最小；红色实线为留一法错判概率曲线，K=7时达到最小。「留一法的曲线基本在旁置法下方，应是较为客观的预测错误估计」。第四幅图是回归预测时测试样本集的均方误差随参数K变化的曲线。

KNN应用——天猫数据集

 

 

library(class) 
Tmall_train<-read.table(file="天猫_Train_1.txt",header=TRUE,sep=",")
head(Tmall_train)
#   BuyOrNot BuyDNactDN ActDNTotalDN BuyBBrand BuyHit
# 1        1       6.38        51.09      2.83   1.57
# 2        1       8.93        60.87      3.20   2.17
# 3        1      16.13        33.70     11.63   6.36
# 4        1      16.22        40.22     11.29   6.25
# 5        1       3.85        56.52      1.89   1.45
# 6        1       4.00        54.35      2.13   1.28
Tmall_train$BuyOrNot<-as.factor(Tmall_train$BuyOrNot)
Tmall_test<-read.table(file="天猫_Test_1.txt",header=TRUE,sep=",")
head(Tmall_test)
#   BuyOrNot BuyDNactDN ActDNTotalDN BuyBBrand BuyHit
# 1        0       0.00        54.84      0.00   0.00
# 2        1       7.69        83.87      2.36   0.83
# 3        1      14.29        90.32      4.76   3.89
# 4        1      10.00        32.26      7.69   4.00
# 5        1      15.38        41.94      8.70   6.98
# 6        0       0.00        19.35      0.00   0.00
Tmall_test$BuyOrNot<-as.factor(Tmall_test$BuyOrNot)

 

 

模型方法同上：

 

 

# 天猫成交顾客的分类预测
set.seed(123456)
errRatio<-vector()   
for(i in 1:30){
 KnnFit<-knn(train=Tmall_train[,-1],test=Tmall_test[,-1],cl=Tmall_train[,1],k=i,prob=FALSE) 
 CT<-table(Tmall_test[,1],KnnFit)
 errRatio<-c(errRatio,(1-sum(diag(CT))/sum(CT))*100)
}
errorRation
# [1] 1.707317 2.195122 2.804878 3.170732 3.292683 4.146341 3.292683 4.878049 5.975610 4.756098 5.365854 6.097561 6.341463 6.341463 6.341463 6.829268 8.048780
# [18] 8.048780 8.048780 8.048780 8.048780 6.951220 6.829268 6.707317 8.048780 7.439024 8.048780 8.048780 8.048780 8.048780
plot(errRatio,type="b",xlab="近邻个数 K",ylab="错判率(%)",main="天猫成交顾客的分类预测")

 

 

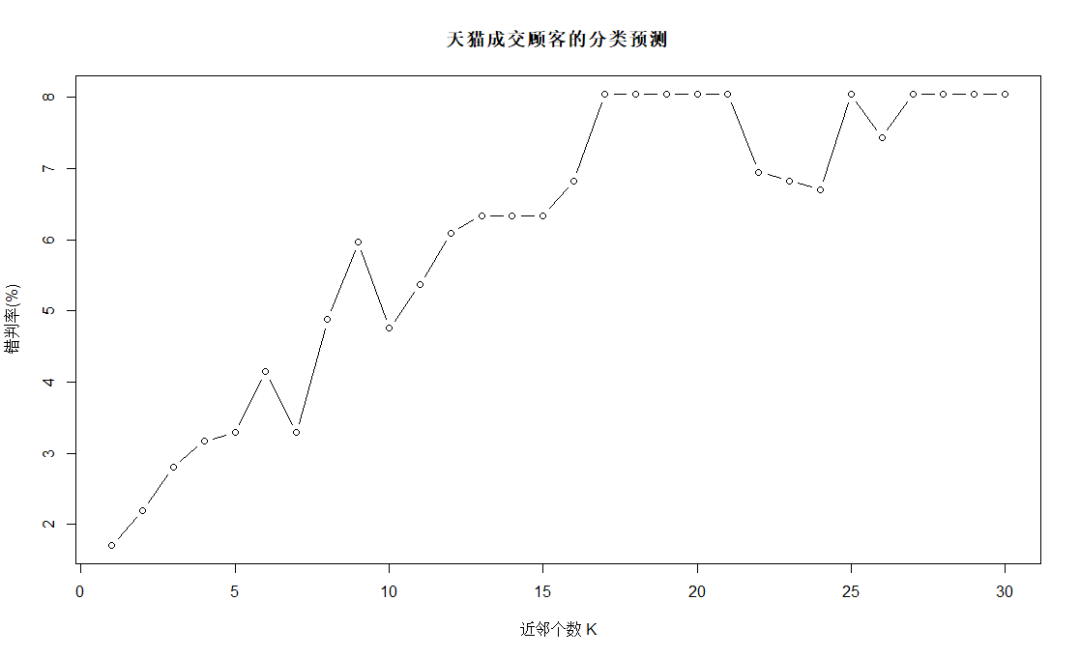
结合上图并兼顾KNN分析的稳健性等考虑，采用K=7的分析结论，错判率为3.3%。

基于变量重要性的加权KNN

KNN默认各输入变量在距离测度中有“同等重要”的贡献，但情况并不总是如此。因此需要采用基于变量重要性的加权KNN，计算加权距离，给重要变量赋予较高的权重，不需要的变量赋予较低的权重是必要的。

天猫数据KNN分类讨论变量的重要性

 

 

library(class)
par(mfrow=c(2,2))
set.seed(123456)
errRatio<-vector()   
for(i in 1:30){
 KnnFit<-knn(train=Tmall_train[,-1],test=Tmall_test[,-1],cl=Tmall_train[,1],k=i,prob=FALSE) 
 CT<-table(Tmall_test[,1],KnnFit) 
 errRatio<-c(errRatio,(1-sum(diag(CT))/sum(CT))*100)    
}
plot(errRatio,type="l",xlab="近邻个数 K",ylab="错判率(%)",main="邻近数 K 与错判率")
# 选择一个错判率相对较低的 K
errDelteX<-errRatio[7]
# 剔除变量
for(i in -2:-5){
 fit<-knn(train=Tmall_train[,c(-1,i)],test=Tmall_test[,c(-1,i)],cl=Tmall_train[,1],k=7)
 CT<-table(Tmall_test[,1],fit)
 errDelteX<-c(errDelteX,(1-sum(diag(CT))/sum(CT))*100)
}
plot(errDelteX,type="l",xlab="剔除变量",ylab="剔除错判率(%)",main="剔除变量与错判率(K=7)",cex.main=0.8)
xTitle=c("1:全体变量","2:消费活跃度","3:活跃度","4:成交有效度","5:活动有效度")
legend("topright",legend=xTitle,title="变量说明",lty=1,cex=0.6)
FI<-errDelteX[-1]+1/4
wi<-FI/sum(FI)
GLabs<-paste(c("消费活跃度","活跃度","成交有效度","活动有效度"),round(wi,2),sep=":")
pie(wi,labels=GLabs,clockwise=TRUE,main="输入变量权重",cex.main=0.8)
ColPch=as.integer(as.vector(Tmall_test[,1]))+1
plot(Tmall_test[,c(2,4)],pch=ColPch,cex=0.7,xlim=c(0,50),ylim=c(0,50),col=ColPch,
     xlab="消费活跃度",ylab="成交有效度",main="二维特征空间中的观测",cex.main=0.8)

 

 

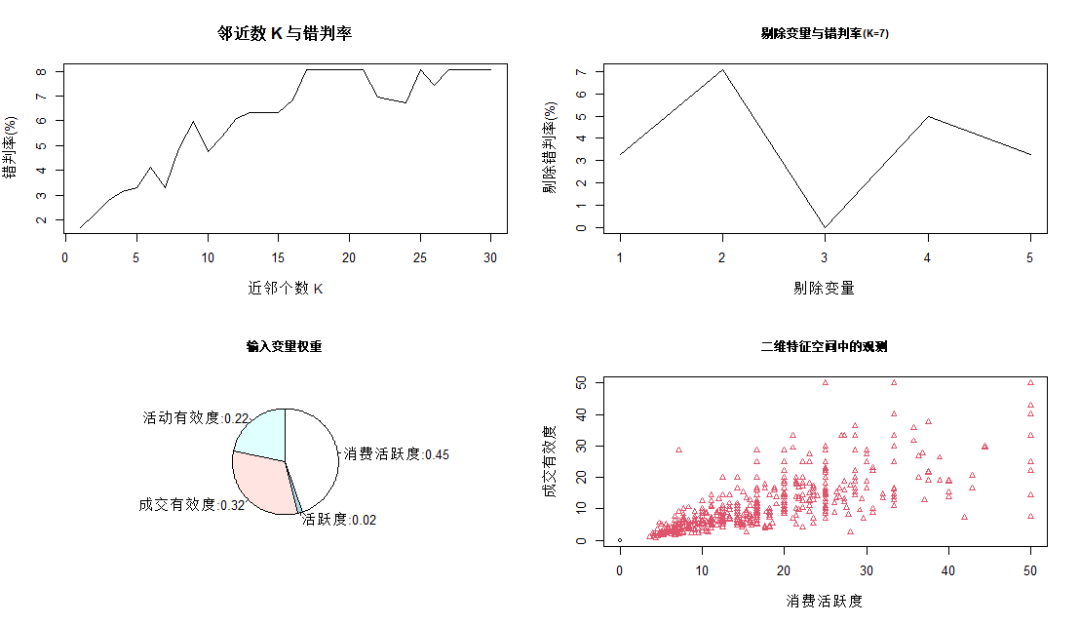
上图中第一幅图为普通KNN方法；

第二幅图为确定K=7后，逐个剔除变量，剔除后的错判率曲线（"1:全体变量","2:消费活跃度","3:活跃度","4:成交有效度","5:活动有效度"），可见剔除消费活跃度后错判概率显著增加，说明消费活跃度对预测的影响巨大；剔除活跃度后错判概率大幅下降，说明该变量包含较强噪声，对预测性能有负面影响；剔除成交有效性后错判率也大幅上升，说明该变量对预测贡献较大；

根据FI定义计算各个输入变量的重要性，确定的权重如第三幅图；第四幅图是消费活跃度和成交有效度特征空间中观测点的分布情况，黑色圆圈表示无成交，红色三角表示有成交，可见所有无交易点均在消费活跃度和成交有效度等于0处，消费活跃度和成交有效度大于0则均为有成交。

❝

综上，结论如下：

①在近邻数K=7时，普通KNN方法对测试样本集的错判率仅为3.3%，效果较好；

②大部分成交顾客处于消费活跃度和成交有效性取值水平较低的位置，在消费活跃度和成交有效性上取值较高处的成交顾客数量很少，可作为日后顾客营销策略的参考依据

❞

基于观测相似性的加权KNN

 

 

# devtools::install_github("KlausVigo/kknn")
library("kknn")
# kknn(formula = R公式, train = 训练样本集, test = 测试样本集, na.action = na.omit(), k = 邻近个数K, distance = k, kernel = 核名称)
par(mfrow=c(2,1))
Tmall_train<-read.table(file="天猫_Train_1.txt",header=TRUE,sep=",")
Tmall_train$BuyOrNot<-as.factor(Tmall_train$BuyOrNot)
fit<-train.kknn(formula=BuyOrNot~.,data=Tmall_train,kmax=11,distance=2,kernel=c("rectangular","triangular","gaussian"),na.action=na.omit())
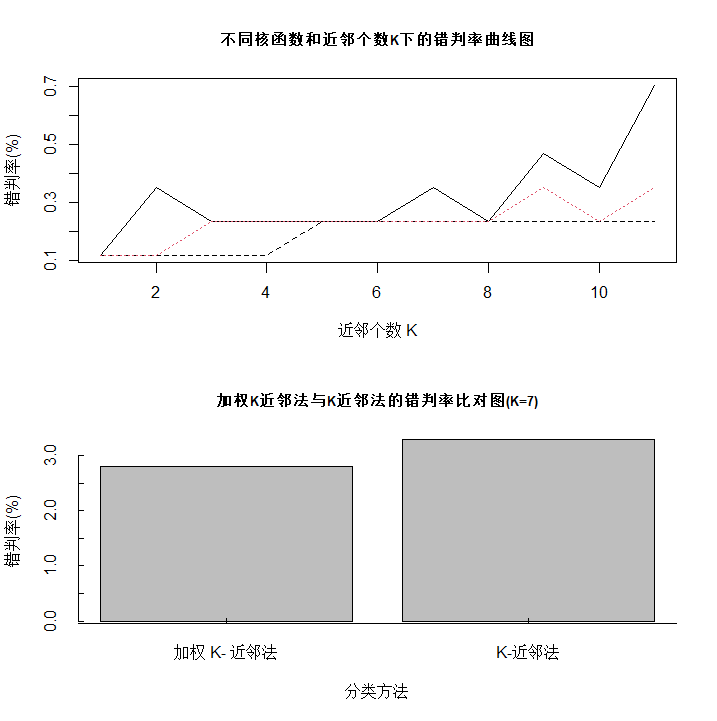
plot(fit$MISCLASS[,1]*100,type="l",
     main="不同核函数和近邻个数K下的错判率曲线图",cex.main=0.8,xlab="近邻个数 K",ylab="错判率(%)")
lines(fit$MISCLASS[,2]*100,lty=2,col=1)
lines(fit$MISCLASS[,3]*100,lty=3,col=2)
legend("topleft",legend=c("rectangular","triangular","gaussian"),lty=c(1,2,3),col=c(1,1,2),cex=0.7)
# 利用加权 K 近邻分类
Tmall_test<-read.table(file="天猫_Test_1.txt",header=TRUE,sep=",")
Tmall_test$BuyOrNot<-as.factor(Tmall_test$BuyOrNot)
fit<-kknn(formula=BuyOrNot~.,train=Tmall_train,test=Tmall_test,k=7,distance=2,kernel="gaussian",na.action=na.omit())
CT<-table(Tmall_test[,1],fit$fitted.values)
errRatio<-(1-sum(diag(CT))/sum(CT))*100
# 利用 K 近邻分类
library("class")
fit<-knn(train=Tmall_train,test=Tmall_test,cl=Tmall_train$BuyOrNot,k=7)
CT<-table(Tmall_test[,1],fit)
errRatio<-c(errRatio,(1-sum(diag(CT))/sum(CT))*100)
errGraph<-barplot(errRatio,main="加权K近邻法与K近邻法的错判率比对图(K=7)",
                  cex.main=0.8,xlab="分类方法",ylab="错判率(%)",axes=FALSE)
axis(side=1,at=c(0,errGraph,3),labels=c("","加权 K- 近邻法","K-近邻法",""),tcl=0.25)
axis(side=2,tcl=0.25)

 

 

决策树&随机森林

原理

决策树的目标是建立分类预测模型或回归预测模型。决策树(decision tree)也称判定树，它是由对象的若干属性、属性值和有关决策组成的一棵树。其中的节点为属性（一般为语言变量），分枝为相应的属性值（一般为语言值）。从同一节点出发的各个分枝之间是逻辑“或”关系；根节点为对象的某一个属性；从根节点到每一个叶子节点的所有节点和边，按顺序串连成一条分枝路径，位于同一条分枝路径上的各个“属性-值”对之间是逻辑“与”关系，叶子节点为这个与关系的对应结果，即决策属性。

「根节点」：决策树最上层的点，一棵决策树只有一个根节点；

「叶节点」：没有下层的节点称为叶节点；

「中间节点」：位于根节点下且自身有下层的节点。中间节点可分布在多个层中，同层节点称为兄弟节点。上层节点是下层节点的父节点，下层节点是上层节点的子节点。根节点没有父节点，叶节点没有子节点。

**2 叉树和多叉树 **：若树中每个节点最多只能长出两个分枝，即父节点只能有两个子节点，这样的决策树称为2叉树。若能长出不止两个分枝，即父节点有两个以上的子节点，这样的决策树称为多叉树。

❝

决策树分为分类树和回归树，分别对应分类预测模型和回归预测模型，分别用于对分类型和数值型输出变量值的预测。

❞

决策树主要围绕两个核心问题展开：

「决策树的生长」。即利用训练样本集完成决策树的建立过程。决策树一般不建立在全部观测样本上，通常需首先利用旁置法，将全部观测样本随机划分训练样本集和测试样本集。在训练样本集上建立决策树，利用测试样本集估计决策树模型的预测误差；

「决策树的剪枝」。即利用测试样本集对所形成的决策树进行精简。

分类回归树的R实现

 

 

rpart(输出变量 ~ 输入变量, data = 数据框名, method = 方法名, parms = list(split = 异质性测度指标), control = 参数对象名)
# 数据事先组织在 data 参数指定的数据框中；
# 输出变量~输入变量 是R公式的写法，若建立分类树，输出变量应为因子，若有多个输入变量，需用加号连接；
# 参数 method 用于指定方法，可取值：“class”表示建立分类树，“position”和“anova”分别输出变量为计数变量和其他数值型变量，此时建立回归树；
# 参数 parms 用于指定分类树的异质性测度指标，可取值：“gini”表示采用Gini系数，“information”表示采用信息熵；
# 参数 control 用于设定预修剪参数、后修剪中的复杂度参数CP值

 

 

设置预修剪等参数的 R 函数：

 

 

rpart.control(minsplit=20, maxcompete=4,xval=10,maxdepth=30,cp=0.01)
# minsplit：指定节点最小样本量，默认为20
# maxcompete：指定按变量重要性降序，输出当前最佳分组变量的前若干个候选变量，默认为4
# xval：指定进行交叉验证剪枝时的交叉折数，默认为10
# maxdepth：指定最大树深度，默认为30
# cp：指定最小代价复杂度剪枝中的复杂度CP参数值，默认为0.01

 

 

❝

当参数 cp 采用默认值 0.01 且 R 给出的决策树过小时（由于0.01过大的结果），可适当减小 cp 参数值。如可指定参数 cp 为 0，此时的决策树是满足预修剪参数下的未经后修剪的最大树，实际应用中这棵树可能过于茂盛。再次基础上，R 将依次给出 CP 值从 0 开始并逐渐增大过程中经过若干次修剪后的决策树。

❞

可视化决策树的 R 函数：

 

 

rpart.plot(决策树结果对象名, type = 编号, branch = 外形编号, extra = 1)
# 决策树对象名：rpart 函数返回对象；
# type：决策树展示方式。可取值：0~4；
# branch：指定决策树外形，可取 0（斜线连接）和 1（垂线连接）；
# extra：指定在节点中显示哪些数据。可取1~9

 

 

复杂参数 CP 对预测误差的影响：

 

 

# 复杂度参数 CP 是决策树剪枝的关键参数，其设置是否合理直接决定决策树是否过于复杂而出现过拟合，或是否过于简单而无法得到理想的预测精度。可通过函数 printcp 和 plotcp 浏览与可视化 cp 值：
printcp(决策树结果对象名)
plotcp(决策树结果对象名)

 

 

分类回归树的应用：提炼不同消费行为顾客的主要特征

1.初建分类树

 

 

# install.packages("rpart")
# install.packages("rpart.plot")
library(rpart)
library(rpart.plot)
BuyOrNot<-read.table(file="消费决策数据.txt",header=TRUE)
BuyOrNot$Income<-as.factor(BuyOrNot$Income) #指定收入为因子
BuyOrNot$Gender<-as.factor(BuyOrNot$Gender) # 指定性别为因子
# 指定预修剪等参数，复杂度参数CP为 0
Ctl <- rpart.control(minsplit=2,maxcompete=4,xval=10,maxdepth=10,cp=0)
set.seed(12345)
TreeFit1 <- rpart(Purchase~.,data=BuyOrNot,method="class",
                parms=list(split="gini"),control=Ctl)
rpart.plot(TreeFit1,type=4,branch=0,extra=2)
printcp(TreeFit1) # 可视化CP值
plotcp(TreeFit1)

 

 

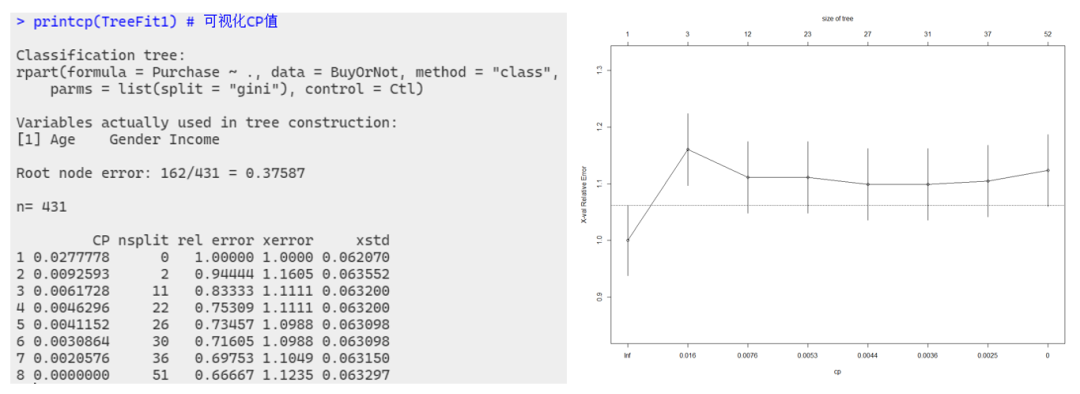
结果显示，根节点包括全部 431 个观测样本，其中 「162 个输出变量值为1的观测被误判为0，错判率为 38%」。左图中，（不含序号）第1列为CP值，第2列 nsplit 为样本数据共经过的分组次数，第3列 rel error 是预测误差相对值的估计，第4列 xerror 是交叉验证的预测误差相对值，第 5 列 xstd 为预测误差的标准误。

需要注意的是，这里的第 3~4 列给出的是以根节点预测误差为单位1的相对值。例如：本例中根节点的预测错误率162/431为单位1，经2次分组得到3个叶节点的分类树，因错误相对值为0.944，所以该树总的预测错误率为153/431。

当复杂度参数 CP 取指定值 0 时，此时的分类树是经过51次分组的结果，包含52个叶节点，与右图对应。此时分类树的预测误差估计值为0.667。经过交叉验证，在CP参数增加至0.002过程中进行了若干次剪枝，此时决策树是36次分组后的结果，包含37个节点，预测误差相对值为0.698，增加了0.031个单位。

右图纵坐标为根节点的交叉验证预测误差为单位 1 时，当前决策树的交叉验证预测误差的单位数；横坐标从右往左是 CP 列表中 8 个 CP 值的典型代表值 β，上方对应的是当前决策树所包含的叶节点个数。可以看出，「包含 12 个叶节点的决策树有最低的交叉验证预测误差」。

2.再建分类树

 

 

set.seed(12345)
# 默认参数
(TreeFit2<-rpart(Purchase~.,data=BuyOrNot,method="class",parms=list(split="gini")))
TreeFit2
rpart.plot(TreeFit2,type=4,branch=0,extra=2)  # 可视化决策树
printcp(TreeFit2)  # 显示复杂度CP参数列表

# 指定 cp=0.008，建立前述包含12个叶节点的决策树
TreeFit3<-prune(TreeFit1,cp=0.008) 
rpart.plot(TreeFit3,type=4,branch=0,extra=2)
printcp(TreeFit3)
plotcp(TreeFit3)

 

 

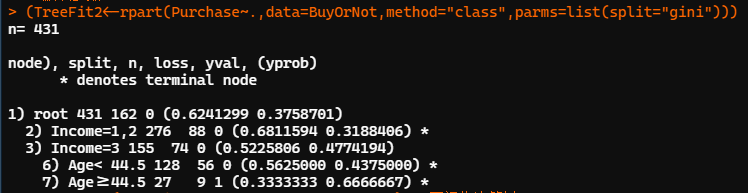
上图是按系统默认参数构建决策树，CP 参数为默认初始值 0.01，异质性指标采用 Gini 系数。节点2后的星号*标记表示为叶节点，其中所有观测的 Income 取 1 或 2，样本量为 276，其中 88 个输出变量为 1 的观测点被误判为 0，置信度为0.68，错判率 0.32。其余同理。

❝

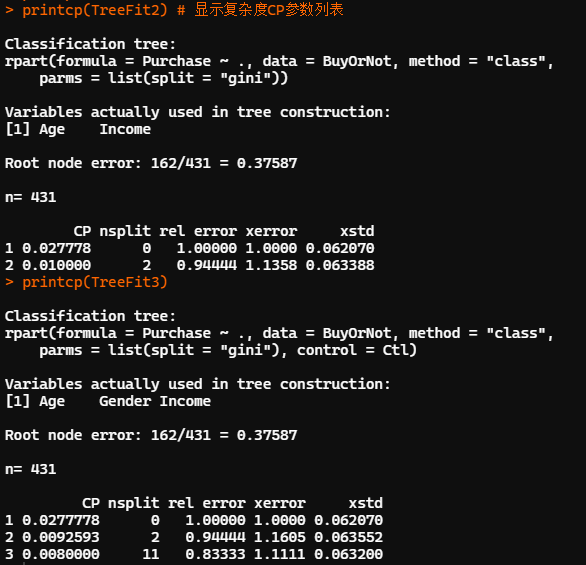
「分类回归树只能建立 2 叉树」

❞

建立分类回归树的组合预测模型：给出稳健预测

分类回归树具有不稳定性，模型会随训练样本的变化而剧烈变动。组合预测模型是提高模型预测精度和稳健性的有效途径，其首要工作是基于样本数据建立一组模型而非单一模型；其次，预测时由这组模型同时提供各自的预测结果，通过类似“投票表决”的形式决定最终的预测结果。

组合预测中的单个模型称为「基础学习器（Base Learner）」，通常有相同的模型形式，如决策树或其他预测模型等。多个预测模型是建立在多个样本集合上的。

如何获得多个样本集合，以及如何将多个模型组合起来实现更合理的“投票表决”，是组合模型预测中的两个重要方面。对此，常见的技术有「袋装（Bagging）技术」和「推进（Boosting）技术」。

1.袋装技术的 R 实现

 

 

# ipred 包中的 bagging 函数
bagging(输出变量名~输出变量名, data = 数据框名, nbagg = k, coob = TRUE, control = 参数对象名)
# 输出变量名~输入变量名为 R 公式的写法，有多个输入变量时应用加号连接；
# coob = TRUE 表示基于袋装观测（OOB）计算预测误差
# control：指定袋装过程所建模型的参数。bagging函数的内嵌模型，即基础学习器为分类回归树，control参数应为rpart函数的参数
# nbagg：指定自举次数为 k，默认重复 25 次自举过程，生成 25颗分类回归树

# adabag 包中的 bagging 函数
bagging(输出变量名~输出变量名, data = 数据框名, mfinal = 重复次数, control = 参数对象名)
# mfinal：指定重复几次自举过程，默认为100。bagging函数的基础学习器为分类树，control参数应为rpart函数的参数
# bagging函数返回值是列表。tree成分中存储k颗分类树的结果；votes中存储k个模型的投票情况；prob中存储预测类别的概率值；class为预测类别；importance为输入变量对输出变量预测重要性的得分
# 对新样本集进行预测：predict.bagging 函数
predict.bagging(bagging 结果对象名, 新样本集名)
# predict.bagging 将返回名为 votes，prob，class的列表成分，含义同bagging函数。此外，还返回名为confusion和error的列表成分，分别存储混淆矩阵和错判率

 

 

2.袋装技术的应用：稳健定位目标客户

 

 

library(rpart)
MailShot<-read.table(file='邮件营销数据.txt',header = T)
MailShot<-MailShot[,-1]  # 剔除ID
Ctl <- rpart.control(minsplit=20,maxcompete=4,maxdepth=30,
                     cp=0.01,xval=10) # rpart的默认参数
set.seed(12345)
TreeFit <- rpart(MAILSHOT~.,data=MailShot,
                 method="class", parms=list(split="gini"))  # 建立单一分类树
rpart.plot(TreeFit,type=4,branch=0,extra=1)
CFit1<-predict(TreeFit,MailShot,type="class")  # 利用单个分类树对全部观测进行预测
# CFit1<-predict(TreeFit,MailShot)  
ConfM1<-table(MailShot$MAILSHOT,CFit1)  # 计算单个分类树的混淆矩阵
#      CFit1
#        NO YES
#   NO  119  46
#   YES  39  96
(E1 <-(sum(ConfM1)-sum(diag(ConfM1)))/sum(ConfM1)) # 计算单个分类树的错判率
# 0.2833333

 

 

首先建立单个分类树，并利用单个分类树对全部观测做预测，错判率为 0.28。

 

 

## 利用ipred包中的bagging建立组合分类树
library(ipred)
set.seed(12345)
MailShot$MAILSHOT <- as.factor(MailShot$MAILSHOT)  # 不转换数据类型一直报错
(BagM1<-bagging(MAILSHOT~.,data=MailShot,nbagg=25,
                coob=TRUE,control=Ctl))  # bagging建立分类组合树
CFit2<-predict(BagM1,MailShot,type="class")  # 利用组合分类树对全部观测进行预测
ConfM2<-table(MailShot$MAILSHOT,CFit2)  # 计算组合分类树的混淆矩阵
(E2<-(sum(ConfM2)-sum(diag(ConfM2)))/sum(ConfM2))  # 计算组合分类树的错判率
# 0.196667

 

 

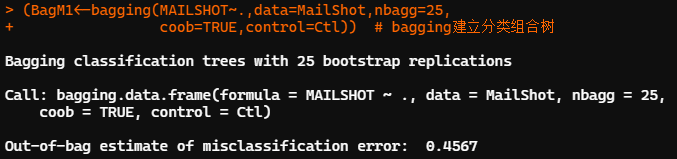
利用 ipred 包中的 bagging 函数建立组合分类树，袋装过程默认进行28次重抽样自举，生成25颗分类树。基于袋外观测（OOB）的预测误差为0.457。利用组合分类树并对全部观测做预测，错判率为 0.197。「预测精度较单一分类树有一定提高」

predict 函数 type 指定为 class 时，给出的预测结果时分类值。不指定参数，默认给出的预测结果是各类别的概率值（预测置信度）。

 

 

## 利用adabag包中的bagging函数
detach("package:ipred")
library(adabag)
MailShot<-read.table(file="邮件营销数据.txt",header=TRUE)
MailShot<-MailShot[,-1]
Ctl<-rpart.control(minsplit=20,maxcompete=4,maxdepth=30,cp=0.01,xval=10)
set.seed(12345)
BagM2<-bagging(MAILSHOT~.,data=MailShot,control=Ctl,mfinal = 25)
BagM2$importance
#       AGE       CAR    GENDER    INCOME   MARRIED  MORTGAGE    REGION      SAVE 
# 17.761337  3.202805  6.126779 49.217348  7.539829  5.398284  8.425630  2.327989 

CFit3<-predict.bagging(BagM2,MailShot)  # 利用组合分类树对全部观测进行预测
CFit3$confusion
CFit3$error

 

 

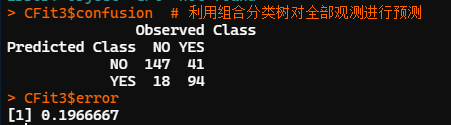
adabag 包中的 bagging 函数建立组合分类树，参数设置同前。函数自动计算了输入变量重要性的测度结果，并进行了归一化处理。输出变量重要性为归一化后的百分比。本例中较为重要的两个输入变量依次为收入（INCOME）和年龄（AGE）。

用组合分类树对全部观测做预测的错判率为 ，预测精度较单一分类树有一定提高。

3.推进技术的 R 实现

袋装技术中，自举样本的生成完全是随机的。多个模型在预测投票中的地位也都相同，未考虑不同模型预测精度的差异性。推进技术在这两方面进行了调整，其中的 AdaBoost（Adaptive Boosting）策略已有较为广泛的应用。

与袋装技术不同的是，AdaBoost 采用的是加权投票方式，不同的模型具有不同的权重，权重大小与模型的预测误差成反比。预测误差较小的模型有较高的投票权重，预测误差较大的模型投票权重较低。可见，「权重越高的模型，对决策结果的影响越大」。

 

 

# adabag 包中的 boosting 函数
boosting(输出变量名~输入变量名, data=数据框, mfinal=重复次数,
        boos=TRUE, coeflearn=模型权重调整方法, control=参数对象名)
# 指定重复自举次数，默认100
# boos = TRUE 表示每次自举过程均调整各观测进入训练样本集的权重
# coeflearn：指定预测时各模型的权重设置方法。可取值 Breiman 或 Freund 或 zhu
# boosting 函数的基础学习器为分类树，control 参数应为 rpart 的默认参数

 

 

bagging函数返回值是列表。tree成分中存储k颗分类树的结果；votes中存储k个模型的投票情况；prob中存储预测类别的概率值；class为预测类别；importance为输入变量对输出变量预测重要性的得分；weight为各个模型的预测权重。

4.推进技术的应用：文件定位目标客户

 

 

library(adabag)
MailShot <- read.table(file="邮件营销数据.txt",header = T)
MailShot<-MailShot[,-1]
MailShot$MAILSHOT <- as.factor(MailShot$MAILSHOT)
Ctl<-rpart.control(minsplit=20,maxcompete=4,maxdepth=30,cp=0.01,xval=10)
set.seed(12345)
BoostM<-boosting(MAILSHOT~.,data=MailShot,boos=TRUE,mfinal=25,
                 coeflearn="Breiman",control=Ctl)
BoostM$importance
#       AGE       CAR    GENDER    INCOME   MARRIED  MORTGAGE    REGION      SAVE 
# 23.666103  3.821141  3.597499 43.118805  5.424618  4.782976 11.057369  4.531490
ConfM4<-table(MailShot$MAILSHOT,BoostM$class)
E4 <- (sum(ConfM4)-sum(diag(ConfM4)))/sum(ConfM4)
E4
# 0.02666667

 

 

本例中，较为重要的两个输入变量依次为收入和年龄。用组合分类树对全部观测做预测的错判率为 0.027，较单一分类树有显著提高。

❝

袋装技术与推进技术有类似的研究目标，但两者训练样本集的生成方式不同，组合预测方式也不同。两者均可有效地提高预测准确性。「在大多数数据集中，推进技术的准确性一般高于袋装技术，但也可能导致过拟合问题。」

❞

随机森林：具有随机性的组合预测

Random Forest 也是一种组合预测模型，是用随机方式建立一片森林，森林中包含众多有较高预测精度且弱相关甚至不相关的决策树，并形成组合预测模型；后续，众多预测模型将共同参与对新观测输出变量取值的预测。

随机森林的内嵌模型，即基础学习器是分类回归树，其特色在于随机，表现在两个方面：

训练样本是对原始样本的重抽样自举，训练样本具有随机性；

在每颗决策树的建立过程中，称为当前最佳分组变量的输入变量，是输出变量全体的一个随机候选变量子集中的竞争获胜者。分组变量具有随机性

「Bagging方法的主要过程：」

训练分类器。从整体样本集合中，抽样n* < N个样本 针对抽样的集合训练分类器Ci

分类器进行投票，最终的结果是分类器投票的优胜结果

随机森林是以决策树为基本分类器的一个集成学习模型，它包含多个由Bagging集成学习技术训练得到的决策树。前面描述了原始的树的bagging算法。Random Forests不同的是：在Bagging的基础上，他们使用一种改进的树学习算法，这种树学习算法在每个候选分裂的学习过程中，选择特征值的一个随机子集。这个过程有时被称为“「feature bagging」”。

以决策树为基本模型的bagging在每次bootstrap放回抽样之后，产生一棵决策树，抽多少样本就生成多少棵树，在生成这些树的时候没有进行更多的干预。而随机森林也是进行bootstrap抽样，但它与bagging的区别是在生成每棵树的时候，每个节点变量都仅仅在随机选出的少数变量中产生。因此，不但样本是随机的，连每个节点变量（Features）的产生都是随机的。

「随机森林分类性能的主要因素：」

森林中单颗树的分类强度（Strength）：每颗树的分类强度越大，则随机森林的分类性能越好。

森林中树之间的相关度（Correlation）：树之间的相关度越大，则随机森林的分类性能越差。

「随机森林的几个理论要点：」

收敛定理。它度量了随机森林对给定样本集的分类错误率。

泛化误差界。单个决策树的分类强度越大，相关性越小，则泛化误差界越小，随机森林分类准确度越高。

袋外估计。Breiman在论文中指出袋外估计是无偏估计，袋外估计与用同训练集一样大小的测试集进行估计的精度是一样的。

「随机森林的优点：」

对于很多种资料，它可以产生高准确度的分类器。

它可以处理大量的输入变量。

它可以在决定类别时，评估变量的重要性。

在建造随机森林时，它可以在内部对于一般化后的误差产生无偏差的估计。

它包含一个好方法可以估计遗失的资料，并且，如果有很大一部分的资料遗失，仍可以维持准确度。

它提供一个实验方法，可以去侦测 variable interactions 。

对于不平衡的分类资料集来说，它可以平衡误差。

它计算各例中的亲近度，对于数据挖掘、侦测偏离者（outlier）和将资料视觉化非常有用。

使用上述。它可被延伸应用在未标记的资料上，这类资料通常是使用非监督式聚类。也可侦测偏离者和观看资料。

学习过程是很快速的。

可以实现并行运行

「随机森林的缺点：」

随机森林已经被证明在某些噪音较大的分类或回归问题上会过拟

对于有不同级别的属性的数据，级别划分较多的属性会对随机森林产生更大的影响，所以随机森林在这种数据上产出的属性权值是不可信的。

由于随机选择属性，得单棵决策树的的预测效果很差

投票机制中，并不是所有的树都能够准确地标记出所有的对象。

「随机森林的应用：」

随机森林是现在研究较多一种数据挖掘算法，由于其良好的性能表现，在现实生活中也获得了广泛的应用。随机森林主要应用于回归和分类。

随机森林的 R 实现

 

 

# randomForest 包中的 randomForst 函数
randomForest(输出变量名~输入变量名, data=数据框名, mtyr=k, ntree=M, importance=TRUE)
# mtry：指定决策树各节点的输入变量个数 k。若输出变量为因子，随机森林中的基础学习器为分类树；若为数值型变量，则基础学习器为回归树；
# ntree：指定随机森林包含 M 颗决策树，默认为 500；
# importance = TRUE：表示计算输入变量对输出变量重要性的测度值

 

 

randomForets 函数的返回值为列表，包含以下成分：

 

 

predicted：基于袋外观测 OOB 的预测类别或预测值；
confusion：基于袋外观测 OOB 的混淆矩阵；
votes：适用于分类树。给出各预测类别的概率值，即随机森林中有多少臂力的分类树投票给第 i 个类别；
oob.times：各个观测值作为 OOB 的次数，即在重抽样自举中有多少次未进入自举样本，其会影响基于袋外观测 OOB 的预测误差结果；
err.rate：随机森林中各个决策树基于 OOB 的整体预测错误率，以及对各个类别的预测错误率；
importance：输入变量重要性测度矩阵。

 

 

随机森林的应用：文件定位客户目标

 

 

library(randomForest)
MailShot<-read.table(file="邮件营销数据.txt", header = T)
MailShot<-MailShot[,-1]
set.seed(12345)
(rFM<-randomForest(MAILSHOT~.,data=MailShot,importance=TRUE,proximity=TRUE))
head(rFM$votes)  # 各观测的各类别预测概率
head(rFM$oob.times)  # 各观测作为 OOB 的次数

 

 

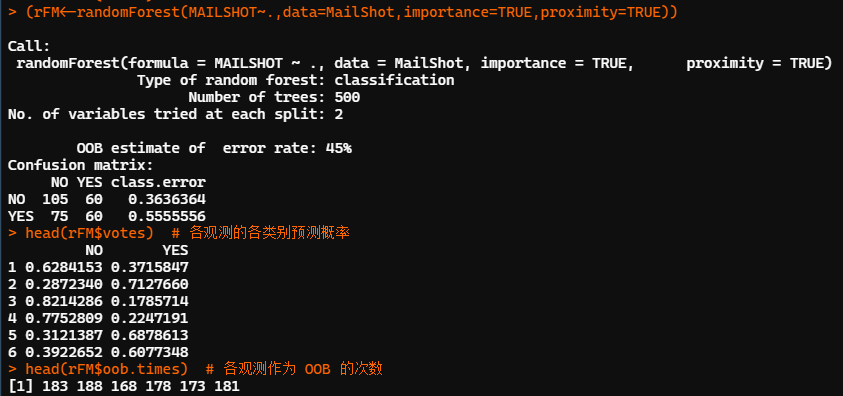
随机森林共建了500颗决策树，每个节点的候选输入变量个数为2。基于袋外观测 OOB 的预测错判率为 45%。从袋外观测的混淆矩阵看，模型对两个类别的预测精度均不理想。对NO类的预测错误率为36.4%，对YES类的预测错误率为55.6%。

以第一个观测为例：有62.8%的决策树投票给NO，37.2%的决策树投票给YES。有183次作为OOB未进入训练样本集。

 

 

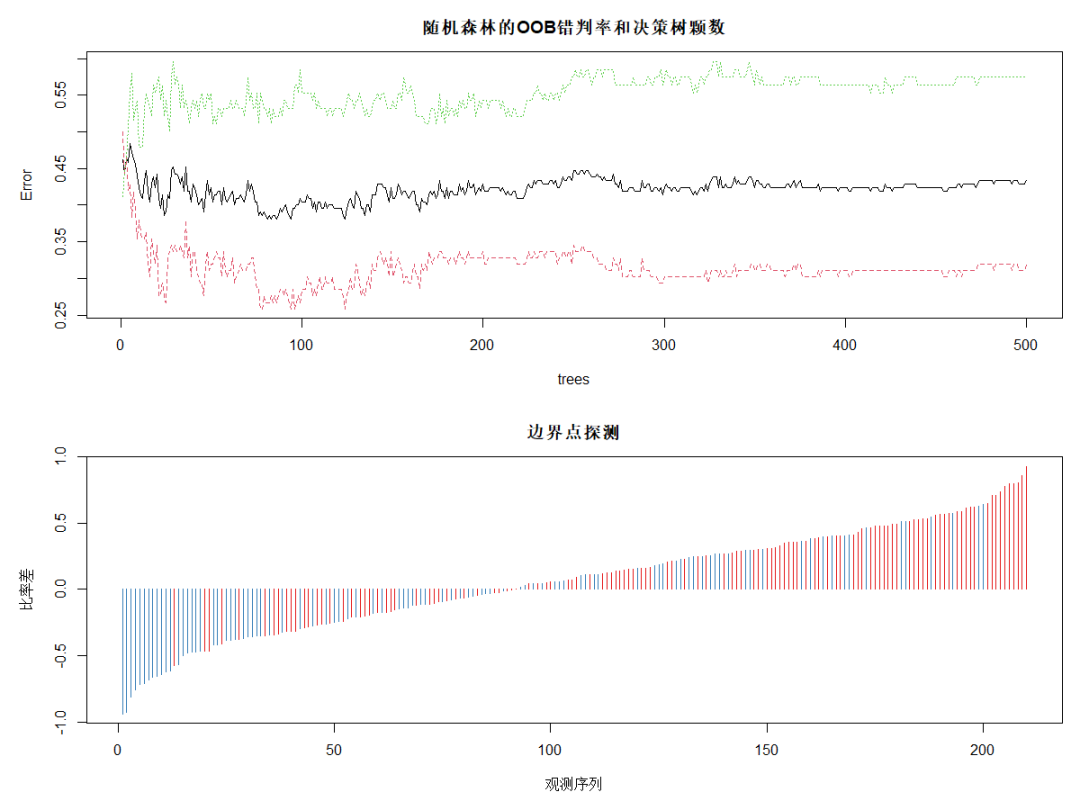
DrawL<-par(mfrow=c(2,1),mar=c(5,5,3,1))
plot(rFM,main="随机森林的OOB错判率和决策树颗数")
plot(margin(rFM),type="h",main="边界点探测",
     xlab="观测序列",ylab="比率差") # 探测边界点
par(DrawL)
Fit<-predict(rFM,MailShot)  # 随机森林对全部观测做预测
ConfM5<-table(MailShot$MAILSHOT,Fit)  # 随机森林对全部观测做预测的混淆矩阵
(E5<-(sum(ConfM5)-sum(diag(ConfM5)))/sum(ConfM5))  # 随机森林的整体错判率
# 0.03

 

 

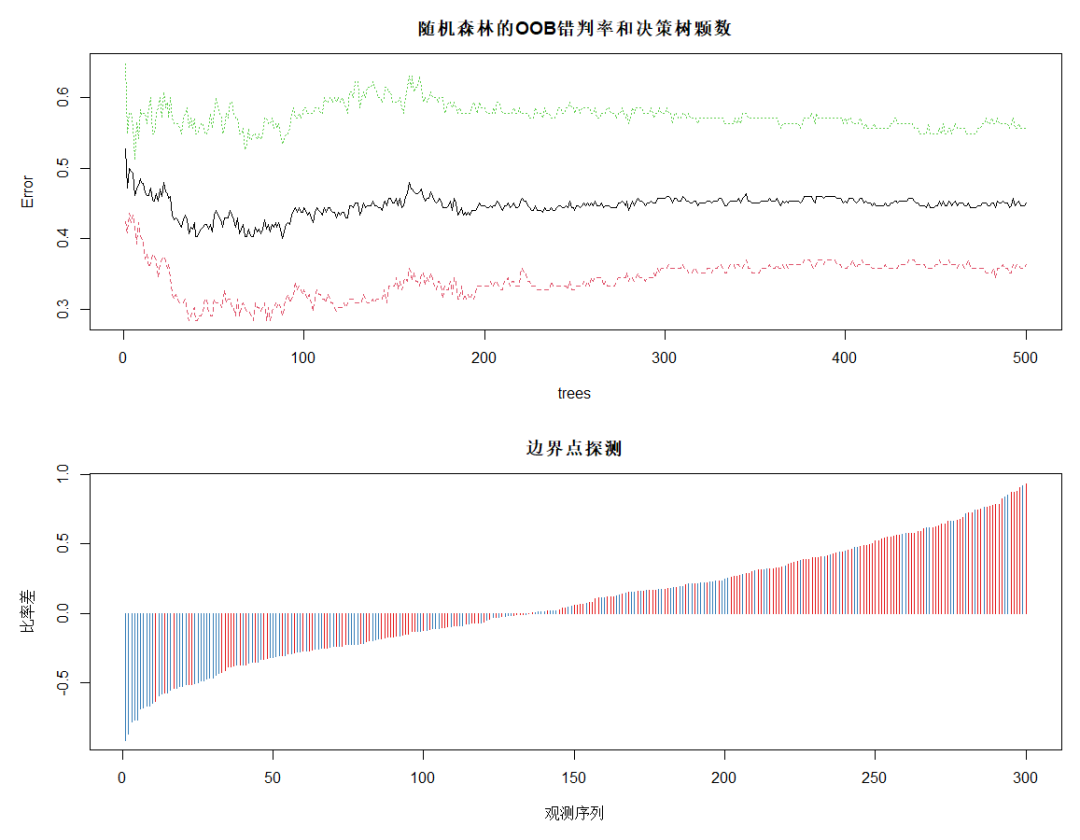
对OOB错判率随随机森林中决策树数量的变化特点进行可视化，plot的绘图数据为err.rate。图中黑色线为整体错判率，红色线为对NO类预测的错判率，绿色线为对YES类预测的错判率。可见，模型对NO类的预测效果好于对整体和YES类的。当决策树达到380以后，各类错判率基本保持稳定。所以本例中参数 ntree 可设置为380。

下面的图为使用 margin 函数考察处于分类边界附近的点的错判情况。该函数以差的升序返回所有观测的比率差。其中，比率差近似等于 0 的观测红色类（NO类）居多，多蓝类（YES类）的预测错误较多。

 

 

head(treesize(rFM))  # 浏览各个树的叶节点个数
head(getTree(rfobj=rFM,k=1,labelVar=TRUE))  # 提取第1颗树的部分信息

 

 

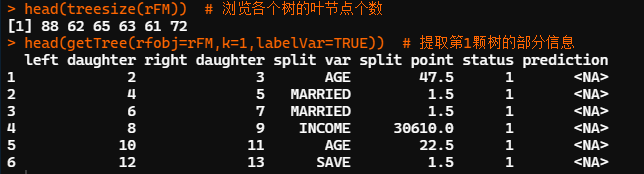
treesize函数可用于显示随机森林中各决策树的大小。treesize(随机森林结果对象名, terminal = TRUE/FALSE)，参数 terminal 取 TRUE 时仅统计决策树的叶节点个数，取 FALSE 表示统计所有节点的个数。

本例中，第 1 颗决策树包含 88 个叶节点。可利用 getTree 函数抽取随机森林中的某颗树并浏览其结构。

 

 

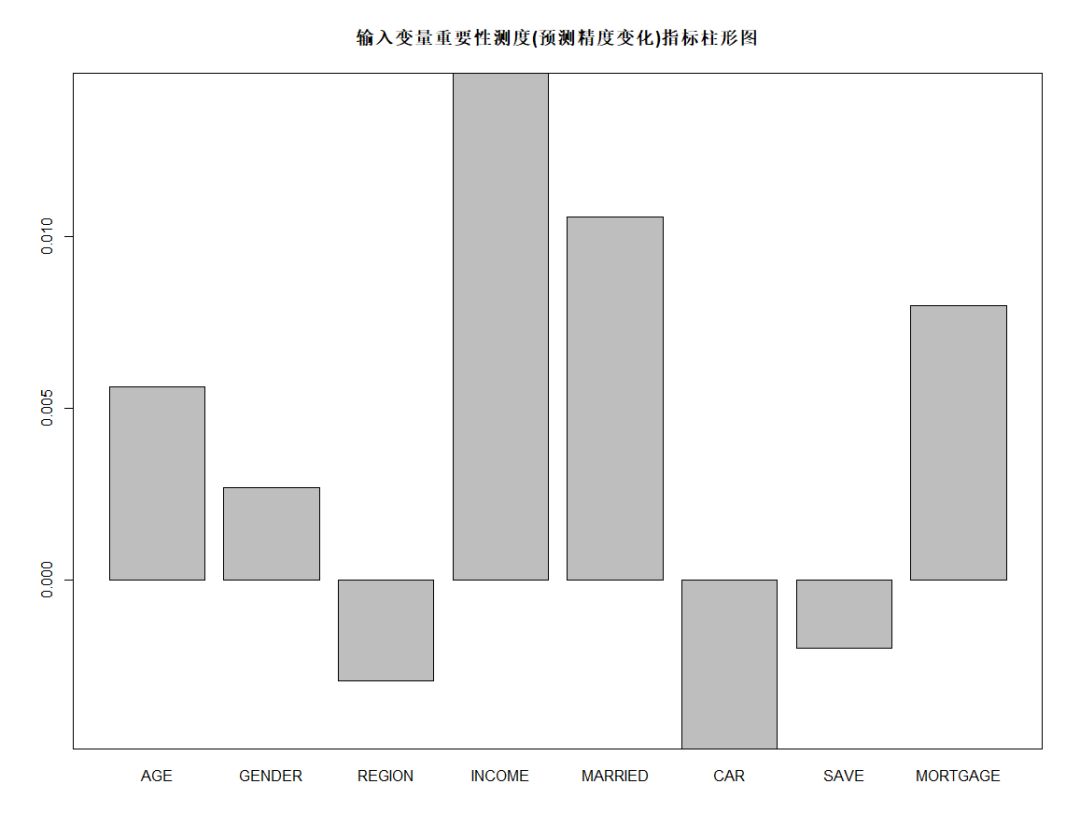
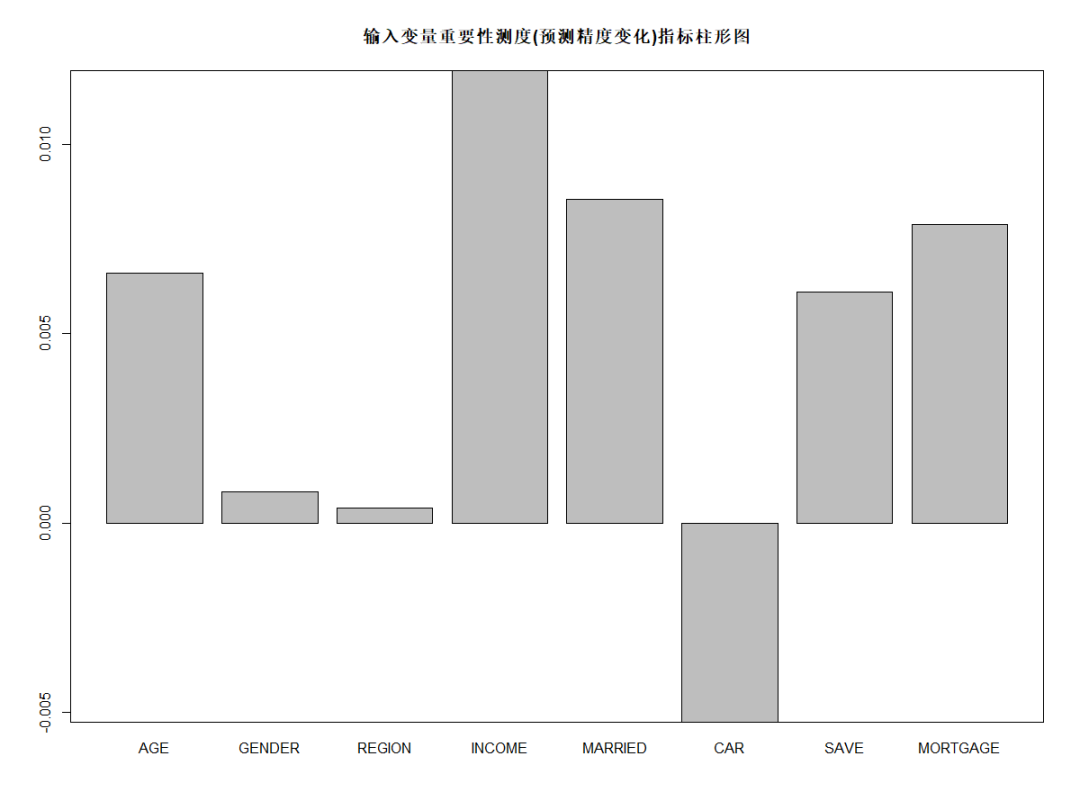
barplot(rFM$importance[,3],
                main="输入变量重要性测度(预测精度变化)指标柱形图")
box()

 

 

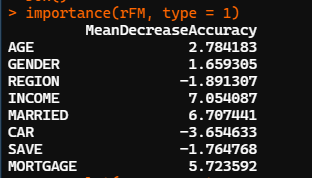
可调用randomForest包中的importance函数，importance(随机森林结果对象名, type=类型编号)。

 

 

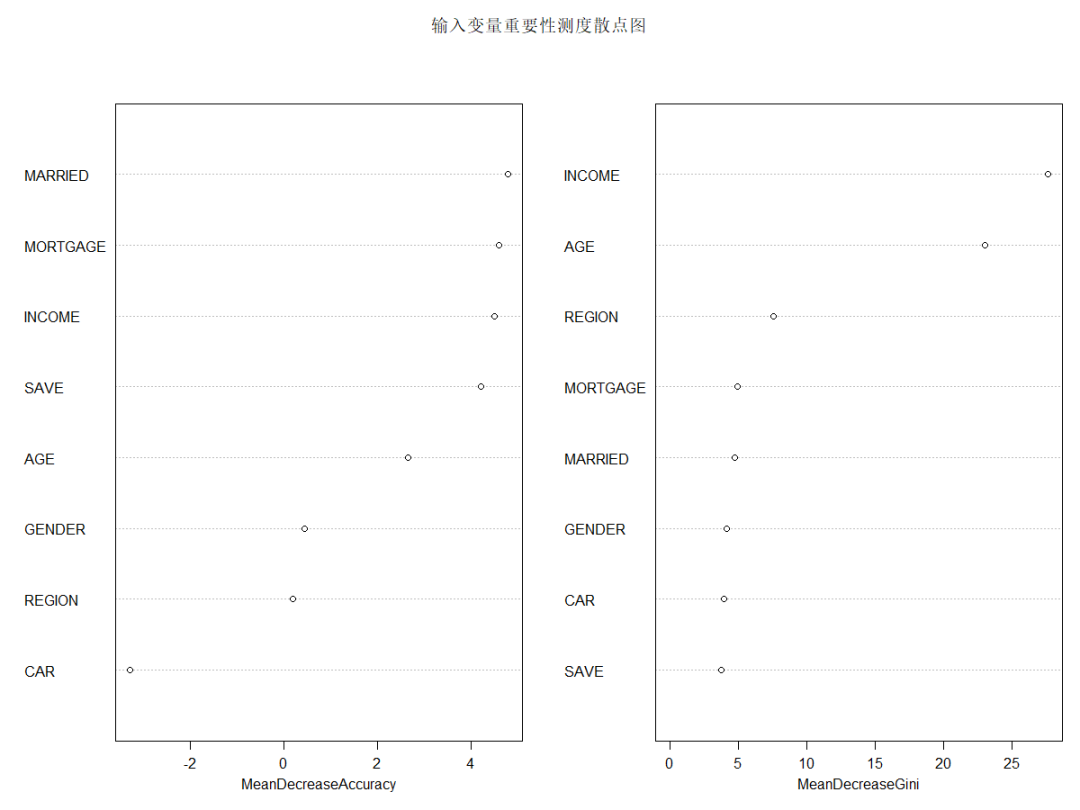
importance(rFM, type = 1)

 

 

 

 

varImpPlot(x=rFM, sort=TRUE, n.var=nrow(rFM$importance), main="输入变量重要性测度散点图")

 

 

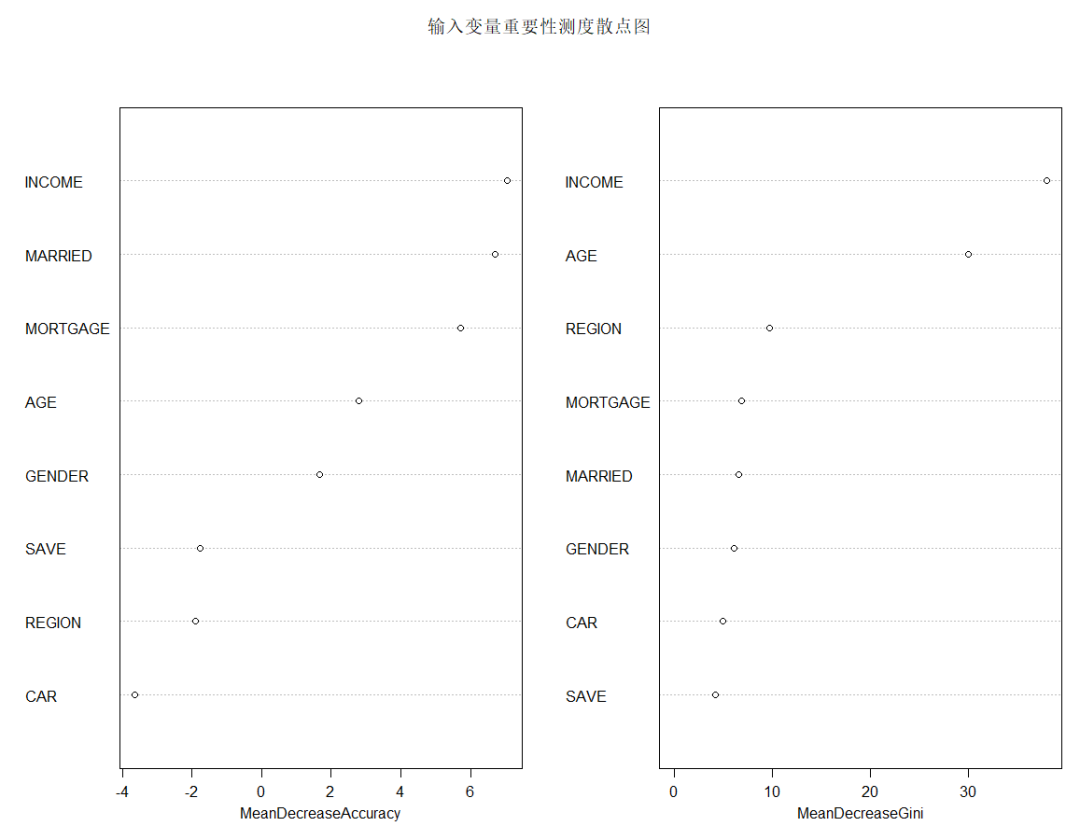
由上图可知，从对输出变量预测精度影响的角度看，收入、是否有债务、婚姻状况较为重要；从对输出变量异质性下降程度看，收入、年龄和居住地较为重要，即收入不同，年龄不同，居住地不同的人群对快递邮件的反应有较大差异。

练习

将上述数据分成70%训练集，训练随机森林模型，并对剩下30%预测，计算预测准确率。并且评价变量重要性。

 

 

library(randomForest)
MailShot<-read.table(file="邮件营销数据.txt", header = T)
MailShot<-MailShot[,-1]
MailShot$MAILSHOT <- as.factor(MailShot$MAILSHOT)
nrow(MailShot)
n <- sample(c(1:300), 300*0.70, replace = F)
MailShot_train <- MailShot[n,]
MailShot_test <- MailShot[-n,]

set.seed(12345)
(rFM<-randomForest(MAILSHOT~.,data=MailShot_train,importance=TRUE,proximity=TRUE))
head(rFM$votes)  # 各观测的各类别预测概率
head(rFM$oob.times)  # 各观测作为 OOB 的次数
DrawL<-par(mfrow=c(2,1),mar=c(5,5,3,1))
plot(rFM,main="随机森林的OOB错判率和决策树颗数")
plot(margin(rFM),type="h",main="边界点探测",
     xlab="观测序列",ylab="比率差") # 探测边界点
par(DrawL)

Fit<-predict(rFM,MailShot_test)  # 随机森林对测试数据做预测
ConfM<-table(MailShot_test$MAILSHOT,Fit)  # 随机森林对测试数据做预测的混淆矩阵
(E<-(sum(ConfM)-sum(diag(ConfM)))/sum(ConfM))  # 随机森林的整体错判率
# 0.4222222

 

 

审核编辑：郭婷