

使用MATLAB进行异常检测(下)
描述
在使用 MATLAB 进行异常检测(上)中,我们探讨了什么是异常值,简单的一维数据异常检测问题,针对高维数据的有监督异常检测方法。 在(下)篇中,我们将和大家一起探讨无监督异常检测。
没有标签怎么办?试试无监督异常检测
参考文档页面:Unsupervised Anomaly Detection[1]
对于没有标签信息的多变量样本数据,在MATLAB 可以使用以下方法检测异常值:
· 马氏距离 (Mahalanobis Distance):
如果数据符合多变量正态分布,可使用样本到数据集分布中心的马氏距离检测异常。利用稳健协方差估计robustcov[2] 函数计算马氏距离,进行离群值检测。
· 局部离群因子 (Local Outlier Factor, LOF):
基于观测点和邻近样本之间的相对密度检测异常点。利用 lof[3] 函数可以创建 LocalOutlierFactor 对象,针对训练数据,直接返回检测结果。
· 孤立森林 (Isolation forest):
通过一组孤立树模型,将异常值和正常数据点隔离。利用 iforest[4] 函数,创建 IsolationForest 对象,针对训练数据,直接返回检测结果。
· 单类支持向量机 (One Class SVM):
在无监督条件下,训练支持向量机模型,在变换后的高维空间,将数据点和原点分离。利用 ocsvm[5] 函数创建OneClassSVM 对象,针对训练数据,直接返回检测结果。
针对测试数据进行异常检测时,使用第一种方法的具体检测步骤将在下文中通过示例说明,如果使用另外三种算法,可以直接调用检测模型的对象函数 isanomaly()。
具体实现方式
1.利用马氏距离检测异常值
【定义】马氏距离:一种衡量样本和数据集分布间相似度的尺度无关的度量指标,例如y到中值点的距离是d2=(y-µ)Σ-1(y-µ)',其中Σ是多维随机变量的协方差矩阵,μ为样本均值。在MATLAB中可通过pdist2函数计算:
d = pdist2(feat,mean(feat),"mahalanobis");
马氏距离可以理解为是对欧式距离的一种修正,假设,下图中蓝色点和黄色点离样本均值的欧式距离相近,但是由于样本整体分布沿 f(x)=x 的方向分布(变量之间具有相关性),蓝色点更有可能是数据集中的点,对应的马氏距离更小,而黄色点更有可能是离群值,对应马氏距离也更大。因此,设定一个合理的阈值,可以划分异常样本和正常样本。
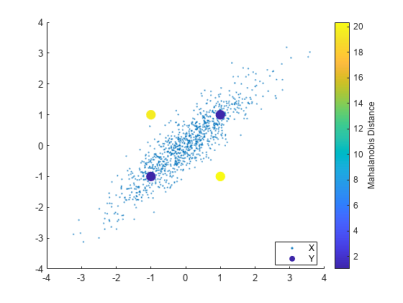
计算马氏距离,首先需要估计 Σ(sig) 和 μ(mu) 。极大似然估计(Maximum Likelihood Estimation, MLE)对数据中的异常值非常敏感,需要采取一种稳健的协方差估计方法,抵抗数据集中存在的异常观测数据。当数据中存在异常值时,协方差行列式偏大。使用最小协方差行列式估计 (Minimum Covariance Determinant, MCD),从 n 个数据样本中,最多选取h个观测值,找到协方差行列式最小的一组观测子集,计算其平均值和协方差,作为估计量。robustcov 函数提供了 FAST-MCD、OGK 和 Olive-Hawkins 三种算法供选择。假设训练数据集中,异常占比为 0.9%:
contaminationFraction = 0.09; [sig,mu,mah,tf] = robustcov(feat, ... OutlierFraction=contaminationFraction);
如果数据符合正态分布的假设,马氏距离的平方值,将服从具有 Dim 个自由度的 χ2 分布,Dim 为原数据的维度。默认情况下,robustcov 函数假设数据符合多变量正态分布,并根据 χ2 分布的临界值,将输入样本的 2.5% 作为异常值,如需调整异常值占比,可以使用 chi2inv 函数,重新计算阈值:
mah_threshold = sqrt(chi2inv(1-contaminationFraction,Dim)); tf_robustcov = mah > mah_threshold;
利用pdist2函数,计算测试集的马氏距离后与阈值mah_threshold进行比较:
dTest = pdist2(featureTestNoLabels.Variables, ... mean(featureTestNoLabels.Variables),"mahalanobis"); isanomalyTest = dTest > mah_threshold; predTest = categorical(isanomalyTest, [1, 0], ["Anomaly", "Normal"]);
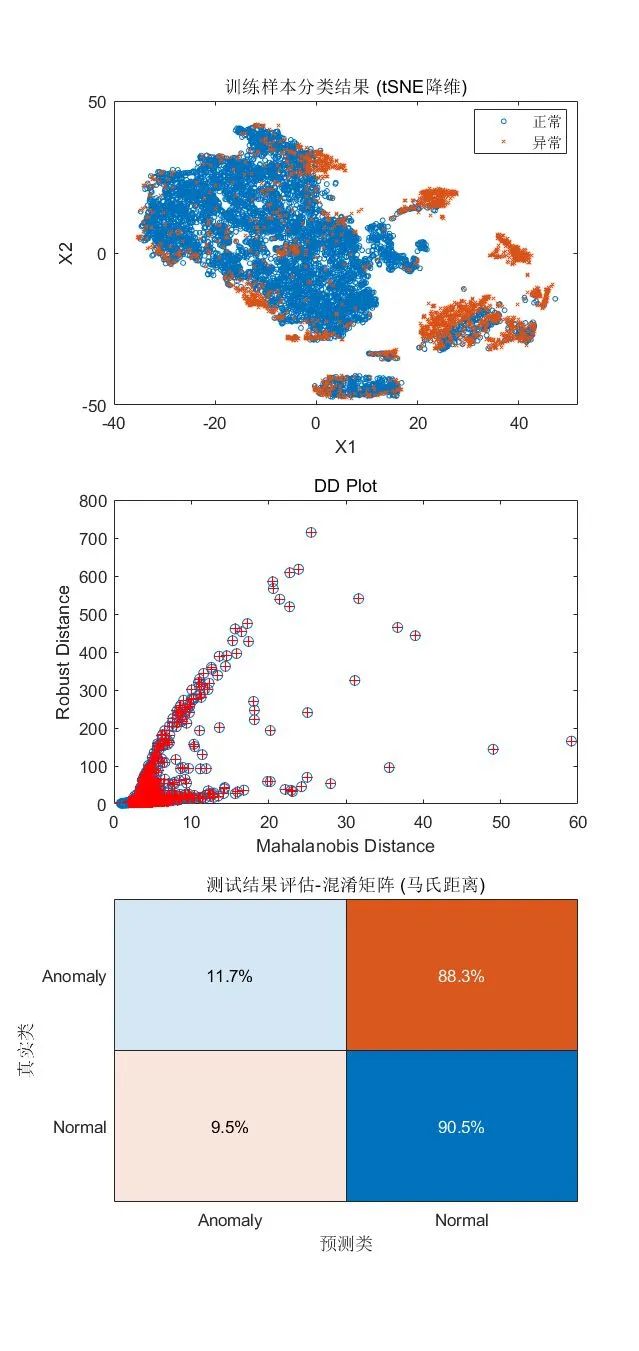
可视化检测结果:
tiledlayout(3,1)
nexttile
gscatter(X(:,1),X(:,2),tf_robustcov,[],'ox',3)
xlabel('X1')
ylabel('X2')
legend({'正常','异常'})
title("训练样本分类结果 (tSNE降维)")
nexttile
plot(d,mah,'o')
line([mah_threshold, mah_threshold], [0, 30], 'color', 'r')
line([0, 6], [mah_threshold, mah_threshold], 'color', 'r')
hold on
plot(d(tf), mah(tf), 'r+')
xlabel('Mahalanobis Distance')
ylabel('Robust Distance')
title('DD Plot')
hold off
nexttile
confusionchart(trueAnomaliesTest, predTest, ...
Title="测试结果评估-混淆矩阵 (马氏距离)", Normalization="row-normalized");
小结
· 以上方法在高维数据上应用效果不理想,可以看到,测试集中异常数据假阴率高。这个方法适用于数据符合或接近正态分布的情况,但是通常情况下,实际数据的分布规律难以预估。
2.局部离群因子
参考文档页面:Local outlier factor model for anomaly detection [6]
该算法通过计算样本 p 和其周围 k 个近邻点的局部可达密度(local reachability density, lrd),即观测样本 p 到近邻点的局部可达距离平均值的倒数:
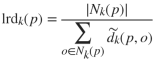
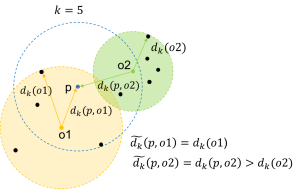
其中,为k近邻集合,样本p关于观测点o的局部可达距离定义为:
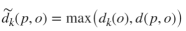
其中 dk(0)为观测点到其近邻的第k个最小距离, d(p,0) 为样本 p 和观测点 o 之间的距离,可参考下图示意。
再根据p的局部可达密度与近邻点的局部可达密度比值的平均值,量化每个样本的离群程度,具体计算可参考以下公式:
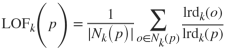
Ird(·)为局部可达密度函数,|Nk(p)|为近邻数量。
因此,对于正常样本,一般 LOF 值小于或接近 1,意味着其局部可达密度和近邻点相近或更高,该样本和邻域内的样本同属一个簇,当 LOF 值大于 1 时,则可能为异常值,利用 ContaminationFraction 参数可调整 LOF 的阈值。
[mdlLOF,tfLOF,scoresLOF] = lof(feat, ... ContaminationFraction=0.09, ... NumNeighbors=1000, Distance="mahalanobis"); [isanomalyLOF,~] = isanomaly(mdlLOF, featureTestNoLabels.Variables); predLOF = categorical(isanomalyLOF, [1, 0], ["Anomaly", "Normal"]);
可视化检测结果:
tiledlayout(3,1)
nexttile
gscatter(X(:,1),X(:,2),tfLOF,[],'ox',3)
xlabel('X1')
ylabel('X2')
legend({'正常','异常'})
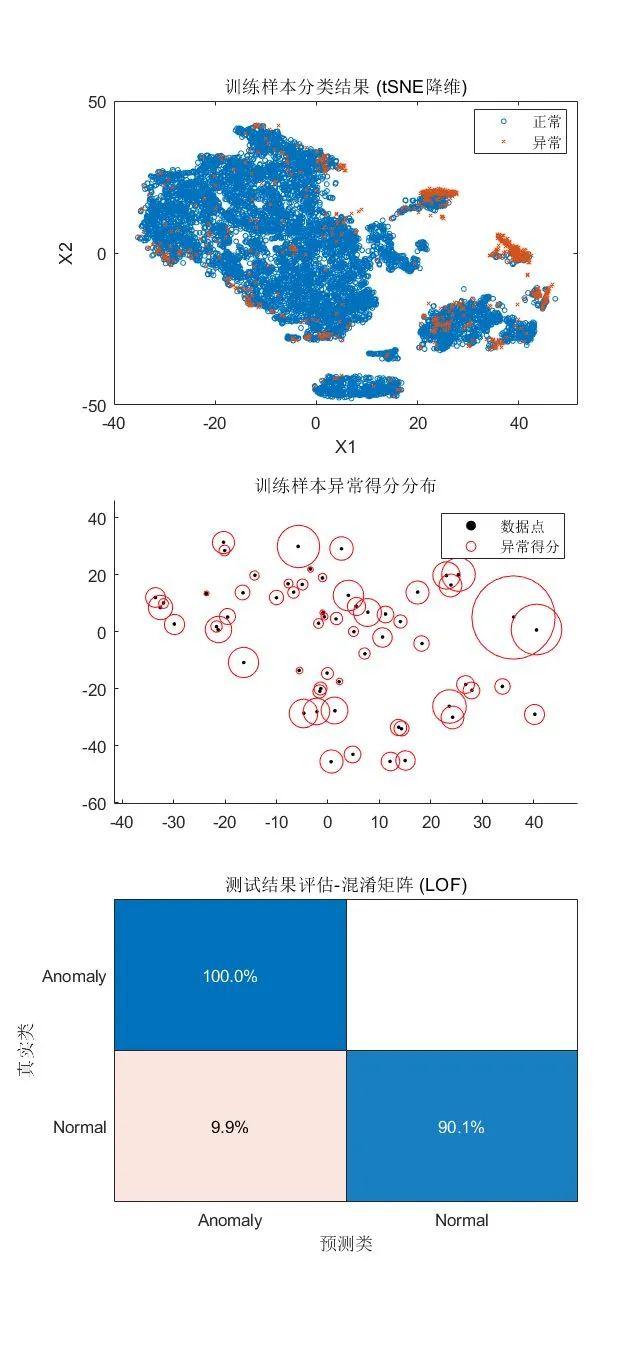
title("训练样本分类结果 (tSNE降维)")
随机选取部分样本,查看对应 LOF 值/异常得分
nexttile
idxes = randi(NumSamples,1,60);
scatter(X(idxes,1),X(idxes,2),5,'filled','MarkerFaceColor','k')
hold on
bubblechart(X(idxes,1),X(idxes,2),scoresLOF(idxes)/100, ...
'r','MarkerFaceAlpha',0);
legend({'数据点','异常得分'})
hold off
title("训练样本异常得分分布")
nexttile
confusionchart(trueAnomaliesTest, predLOF, ...
Title="测试结果评估-混淆矩阵 (LOF)", Normalization="row-normalized");
小结
· 优点:不受数据分布的影响,同时考虑了数据集的局部和全局属性,比较适用于中等高维的数据集,针对示例数据集的预测准确度比较理想。
· 使用限制:对近邻参数较为敏感,由于需要计算数据集中任意两个数据点的距离,算法的时间复杂度较高,在大规模数据集上效率偏低,适合小规模到中等规模的数值型数据。
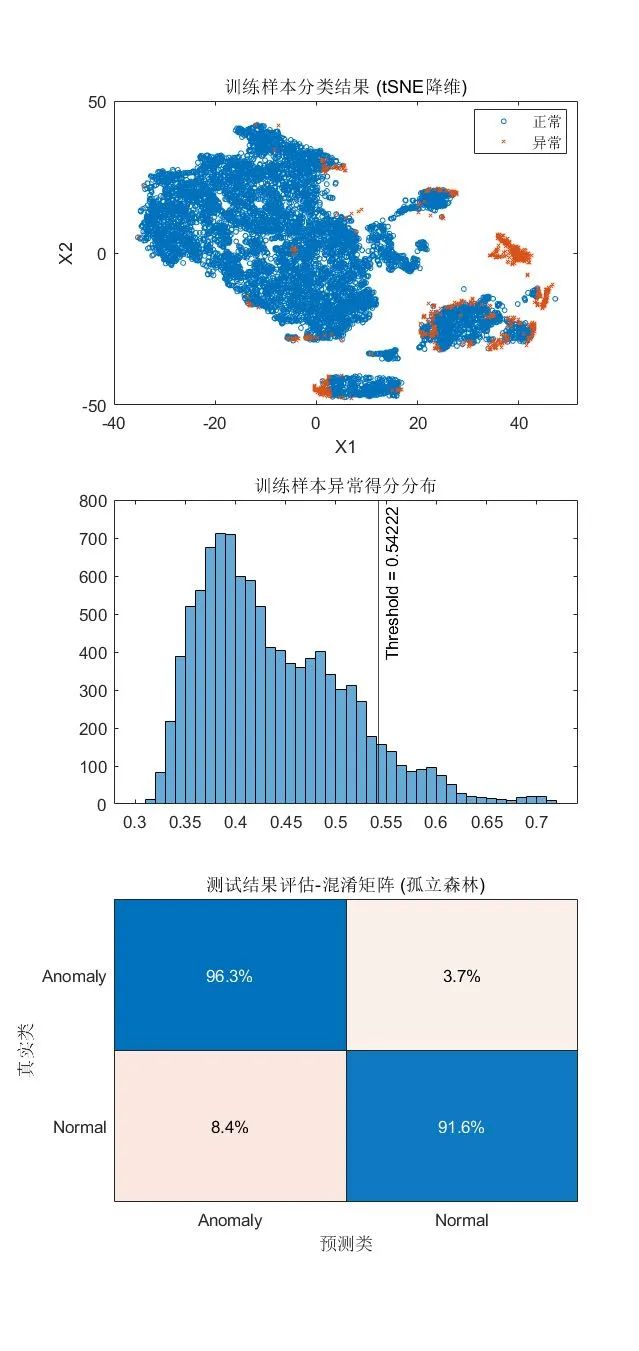
3.孤立森林
参考文档页面:Anomaly Detection with Isolation Forest [7]
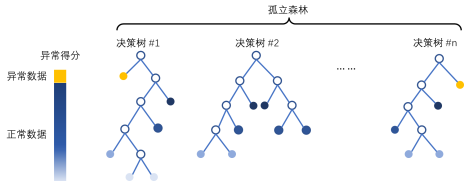
孤立森林算法中,集成了多个决策树模型,训练时,每个决策树对一个不放回采样的数据子集进行分裂,以试图将每一个观测样本划分到一个对应的叶节点上。假设异常点与其他正常数据差异较大,从根节点到对应叶节点需要经过的路径长度 (path length) 相对较短,对于每个样本,将孤立森林中的多个决策树路径长度的平均值,定义为对应样本的异常得分 (anomaly score)。
[mdlIF,tfIF,scoreTrainIF] = iforest(feat, ContaminationFraction=0.09); [isanomalyIF,~] = isanomaly(mdlIF, featureTestNoLabels.Variables); predIF = categorical(isanomalyIF, [1, 0], ["Anomaly", "Normal"]);
可视化检测结果:
tiledlayout(3,1)
nexttile
gscatter(X(:,1),X(:,2),tfIF,[],'ox',3)
xlabel('X1')
ylabel('X2')
legend({'正常','异常'})
title("训练样本分类结果 (tSNE降维)")
nexttile
histogram(scoreTrainIF)
xline(mdlIF.ScoreThreshold,"k-",join(["Threshold =" mdlIF.ScoreThreshold]))
title("训练样本异常得分分布")
nexttile
confusionchart(trueAnomaliesTest, predIF, ...
Title="测试结果评估-混淆矩阵 (孤立森林)", Normalization="row-normalized");
小结
· 优点:适合高维表格数据,不需要计算关于距离和密度的指标,具有线性时间复杂度,每个决策树可独立采样,支持并行化处理来实现加速。
· 使用限制:孤立森林适用于训练集和测试集中,正常样本和异常样本占比接近的情况,且异常样本的特征与正常样本差异很大。
4.单类支持向量机
参考文档页面:Fit one-class support vector machine (SVM) model for anomaly detection [8]
单类支持向量机,或无监督支持向量机,构建决策边界,将训练集中的数据点尽可能划分为一个类别,位于决策边界之外的数据则为异常值。
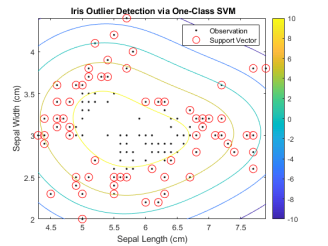
策略是通过核函数将数据映射到新的高维特征空间,在数据与原点间构建超平面(n 维平面)。因为,在低维空间中的非线性特征往往不是线性可分的,在扩展到高维空间后是可分的。在 MATLAB 中,一种实现方法是使用用于构建标准的支持向量机分类模型的 fitcsvm 函数(MATLAB R2022b前),另一种实现方法是使用 ocsvm 函数(MATLAB R2022b 起)。
fitcsvm 函数的求解是基于 SVM 的对偶问题形式,需要求解每对样本的格拉姆矩阵(Gram Matrix),相关示例可在 MATLAB 命令行输入以下指令打开:
>> openExample('stats/DetectOutliersUsingSVMAndOneClassLearningExample')
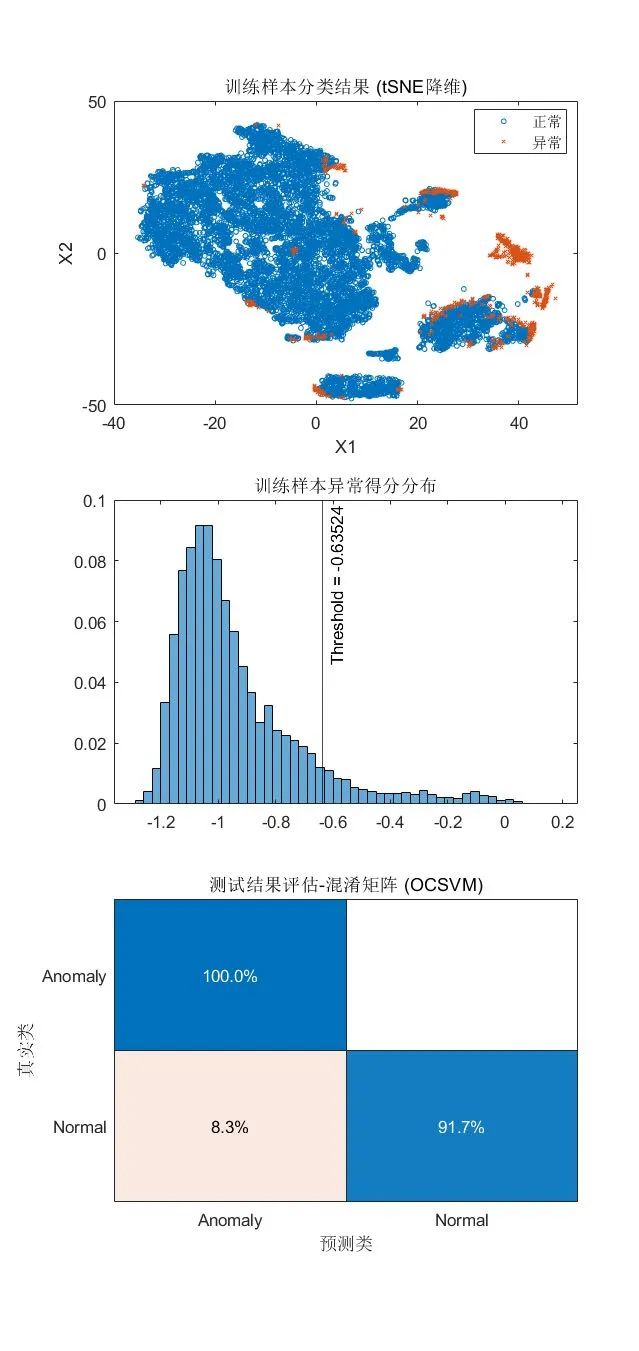
ocsvm 函数的求解则是基于 SVM 的原型问题形式,并使用高斯核进行一类学习,以找到决策边界,针对大规模数据集,求解效率更高。将 KernelScale 设为 "auto" 以启发式地选取合适核函数参数。
[mdlSVM,tfOCSVM,scoreTrainOCSVM] = ocsvm(feat, ...
ContaminationFraction=0.09, ...
StandardizeData=true,KernelScale="auto");
[isanomalyOCSVM,~] = isanomaly(mdlSVM, featureTestNoLabels.Variables);
predOCSVM = categorical(isanomalyOCSVM, [1, 0], ["Anomaly", "Normal"]);
可视化检测结果:
tiledlayout(3,1)
nexttile
gscatter(X(:,1),X(:,2),tfOCSVM,[],'ox',3)
xlabel('X1')
ylabel('X2')
legend({'正常','异常'})
title("训练样本分类结果 (tSNE降维)")
nexttile
histogram(scoreTrainOCSVM, Normalization="probability")
xline(mdlSVM.ScoreThreshold,"k-", ...
join(["Threshold =" mdlSVM.ScoreThreshold]))
title("训练样本异常得分分布")
nexttile
confusionchart(trueAnomaliesTest, predOCSVM,...
Title="测试结果评估-混淆矩阵 (OCSVM)", Normalization="row-normalized");
小结
· 优点:可以处理高维数据,适合表格/结构化数据。
· 使用限制:分类变量需要先转换为虚拟变量(哑变量,Dummy Variable),ocsvm函数中可定义相关参数CategoricalPredictors ,以自动进行转换。
结果对比
在该数据集的离群值检测问题中,孤立森林、局部离群因子与单类支持向量机的结果比较接近,各自的准确度都比较理想,预测结果的重合度也超过了90%:
mean((predIF==predLOF) & (predLOF==predOCSVM))
ans = 0.9325
利用马氏距离/稳健协方差估计的方法,结果不理想,与其他三个算法的结果差异较大:
mean((predIF==predLOF) & (predLOF==predOCSVM) & (predOCSVM==predTest))
ans = 0.6196
综上,各个方法的适用范围不一,或是有特定的使用条件,在使用时需要多加留意,例如马氏距离适合符合正态分布假设的数据集,孤立森林适用于处理正常样本和异常样本差异较大的情况,各个算法计算复杂度有些许区别,可以根据实际情况选择合适的方法。
关键点回顾
· 在处理异常检测问题时,首先需要充分了解您的数据
· 如果您有足够的标注数据(包括异常),可使用有监督学习方法进行异常检测
· 如果您的数据大部分都是正常数据,或者异常数据难以获取或标记,则可以考虑使用无监督的异常检测方法
审核编辑:汤梓红
-
matlab2009下载地址2010-03-22 0
-
如何使用部分异常观测数据进行异常检测2020-04-26 0
-
如何利用MATLAB和Simulink进行S模式检测和解码?2021-05-18 0
-
如何利用MATLAB和Simulink去进行S模式检测和解码?2021-05-20 0
-
基于密集人群的异常实时检测2017-12-18 620
-
检测域划分的虚拟机异常检测算法2017-12-20 656
-
密度偏倚抽样的局部距离异常检测算法2017-12-25 773
-
AIS数据在船舶异常行为检测2018-01-08 1117
-
如何进行双侧空间窗的异常检测详细方法概述2019-01-11 782
-
什么是异常检测_异常检测的实用方法2019-06-29 18666
-
使用MATLAB进行线性编程2021-05-27 566
-
如何选择异常检测算法2021-10-25 1683
-
使用MATLAB进行异常检测(上)2022-11-17 3489
-
采用基于时间序列的日志异常检测算法应用2022-12-09 1644
-
哈工大提出Myriad:利用视觉专家进行工业异常检测的大型多模态模型2023-11-21 1908
全部0条评论

快来发表一下你的评论吧 !

