

电报方程可以干什么呢?
描述
传输线方程,即电报方程,如下所示。
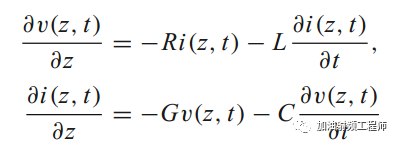
那电报方程可以干什么呢?
电报方程可用于推导传输线上电压和电流的波动方程。
所谓波动方程,其是一个微分方程,它将一个量在时间上的二阶导数与其在空间上的二阶导数相关联。
波动方程的解在时间和空间上都是正弦波。
想象一下,如果你站在海浪中,观察你所在位置海浪的深度变化。会发现海浪的深度变化表现为近似正弦变化。
那是因为波随时间呈正弦曲线。

或者,如果咔嚓一下,时间暂停。
但是你可以运动,你从海岸向大海移动时,你会看到不同位置处的海浪深度也成近似正弦变化。
这是因为波在空间中也是正弦曲线。
为了推导传输线上电压和电流的波动方程,我们从电报方程开始。
如上图所示,这些方程只有一阶导数项,我们知道对于波动方程,我们需要二阶导数。
于是,做如下的推导。

从上面的推导,得到了传输线上电压和电流的波动方程,两者具有相同的微分方程。
获得上述波动方程的解后,即能得到传输线上的电压和电流。

可以看到,γ为复传播常数,且与频率相关。
进而,可以得到:
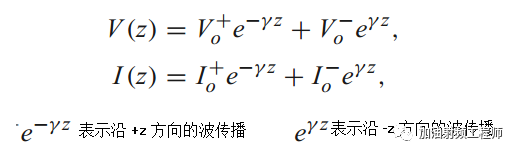
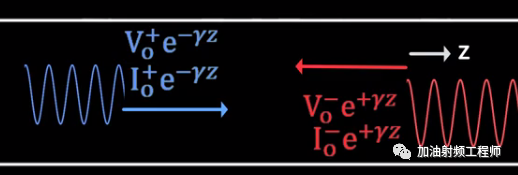
需要注意的是,最后的结果还需加上ejwt,所以是:
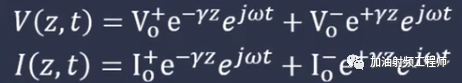
时域表达式为:

由上式可知,同一方向上的电流具有相同的衰减因子和相位,所以,可以假定同一方向上的电压与电流的比值,为一恒定的值。
而且该值只与传输线本身的特性相关,即与分布参数R,G,L,C相关。即:
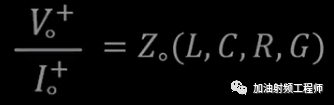
如果只看沿+z轴传播的正向波时,可以得到:

定义:
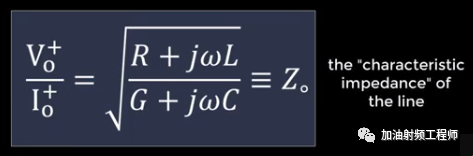
如果传输线是无耗的,即R=G=0,则特征阻抗为实数,如下图所示。
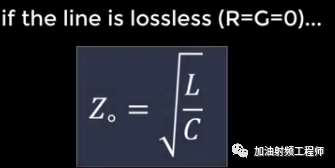
同样的,对于反向传播波
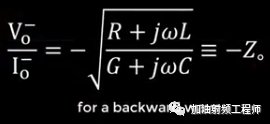
也就是说,从传输线的电报方程,我们可以推导出有关电压和电流的波动方程。
假设电流和电压为简谐波,可以求得电压和电流的表达式。
从电压和电流的表达式,可以得到传输线的特性阻抗。
审核编辑 :李倩
-
这些坏的板,能干什么,还可以改造吗?2015-11-19 0
-
sim808可以干什么2016-07-25 0
-
LABVIEW里面做吉利时的源表的程序时用node是干什么的?node in和node out是干什么的?2017-12-11 0
-
覆铜板是干什么的2020-01-07 0
-
固态硬盘与内存条这两者都是干什么用的呢?2021-06-18 0
-
单片机可以干什么?如何学习单片机?2022-02-15 0
-
STM32CubeMonitor这个工具是干什么的呢2022-03-01 0
-
晶圆厂是干什么的2018-03-16 105501
-
特殊电阻可以干什么?资料下载2021-03-28 857
-
转换器是干什么用的2021-10-01 22998
-
光缆是干什么用的?选购光缆需要注意哪些?2023-03-17 1830
-
光缆是干什么用的?315过后要正确选购2023-03-27 1826
-
什么是阻焊,阻焊的目的是干什么2023-08-28 7289
-
云服务器是干什么的2024-02-18 1481
-
美国云服务器是干什么的2024-02-19 435
全部0条评论

快来发表一下你的评论吧 !

