剖析RF DAC分辨率的真相：是14位还是16位

本应用笔记使用常用数据转换定理分析分辨率和采样速率对带限信号生成应用的影响。结论是，由于16位LVDS接口总线，SNR性能的提高比14位接口总线提供了改进的信噪比（SNR）。

介绍

Maxim Integred生产一系列16位射频数模转换器（RF DAC），旨在提供高性能、宽带信号生成。该系列中的首款器件是MAX5868，于2012年推出，采用并行16位双数据速率（DDR）低压差分信号（LVDS）接口总线。 图1所示为MAX5868数据资料中的简化框图。

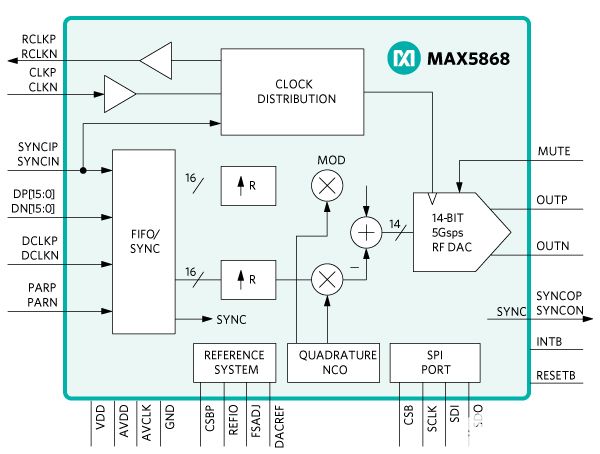
图1.MAX5868简化框图

设计的一个方面导致了一个经常重复的问题：为什么MAX5868的接口是16位，而DAC显示为14位？一个简短而甜蜜的解释是，本底噪声由量化噪声、热噪声和抖动噪声（时钟噪声）决定。如果输入接口只有14位，则量化噪声将主导热噪声。

数据转换器的分辨率直接影响器件的SNR性能。对于DAC，输出噪声有三个主要来源：热噪声、抖动噪声和量化噪声。这些源组合在一起以确定总SNR，如以下计算所示：

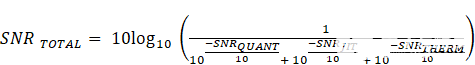
等式 1

哪里：

信 噪 比量化= 由于量化
信噪比吉特= 时钟抖动信
噪比引起的信噪比热= 热噪声引起的信噪比

数据转换中的另一个常见定理是计算理想SNR作为器件分辨率的函数，假设没有热或抖动贡献;换句话说，仅由于量化（SNR）引起的SNRQ） 如下：

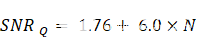
等式2

哪里：

N = 分辨率位数。

虽然公式2最常提及模数转换器（ADC），但它在确定DAC应用中量化噪声的影响时同样有用。应用于DAC的计算结果是整个奈奎斯特带宽内由于量化而产生的总噪声。

量化产生的SNR是有用的信息，但我们需要将其与公式1中的其他项进行比较，以确定DAC和输入接口分辨率的影响。我们还需要考虑各个阶段的更新率，以使比较有意义。为了便于分析，我们将转换计算出的信噪比Q达到理想的噪声频谱密度（NSDQ） 由于量化。我们还将估计信噪比的水平热（NSDT） 项，将与之进行比较量化噪声。

结果将显示 NSDQMAX5868每级的电平确保热噪声占主导地位，并且没有必要进一步提高内核DAC分辨率。

通过量化计算噪声频谱密度

噪声频谱密度是指定带宽内噪声功率的量度，通常以dBm或dBmV表示，通常归一化为1Hz。由于这是一个绝对功率，我们将使用DAC的满量程输出功率规格作为参考点，允许SNR的转换Q由于量化引起的噪声密度。

转换为NSD的第一步是计算奈奎斯特带宽内量化引起的总噪声功率。我们将此术语称为PQ并按如下方式计算：

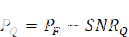
等式 3

哪里：

PF= DAC的输出功率规格，单位为dBm，基于满量程正弦波。

下一步是将噪声功率转换为功率谱密度值。我们假设噪声均匀分布在转换器的奈奎斯特区，并在以下等式中使用它：

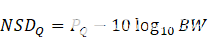
等式 4

哪里：

BW = 奈奎斯特频率

现在，我们用MAX5868规格应用上述理论。首先，我们将研究独立于输入接口的内核14位DAC。然后，我们将检查输入接口，看看分辨率和采样率如何影响性能。

MAX5868的满量程输出功率规格为0dBm，当使用4.96Gsps更新速率产生100MHz正弦波时。计算NSD所需的三个方程的参数问14（等式 2、3 和 4）如下：

N = 14，DAC 内核分辨率，（等式 2）
PF= 0，DAC满量程输出功率（PF） （公式 3） 带宽 = 2.48GHz， f代数转换器/2（公式4）

替换这些值将得到以下结果。

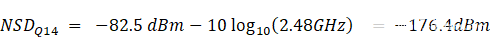
现在让我们看看 NSD问16，输入接口的噪声密度使用16位。首先注意到，Maxim的16位RF DAC产品均在输入接口和DAC内核之间采用插值。插值的使用降低了输入数据的频率，从而降低了奈奎斯特带宽。Maxim RF DAC产品组合的插值速率范围为DAC输入数据速率的4倍至24倍（f数据).MAX5868器件的输入数据速率上限为625MHz，DDR。DDR 数据作为复数值发送到 DAC：16 位 I 和 16 位 Q，按时间交错。它们通过复数调制器组合，提供625MHz（625MHz I + 625MHz Q = 625MHz BW）的奈奎斯特带宽。将公式2和4中的这些值（16位和625MHz带宽）代入得到NSD问16-182.5分贝。

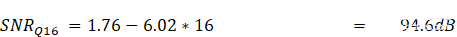
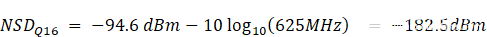
我们现在已经计算了两个信噪比值Q将用于计算两个信噪比总值，一个用于输入分辨率（16 位），一个用于输出（14 位）。接下来，我们将确定DAC输出端的热噪声贡献。计算热噪声的常用定义如下式给出：

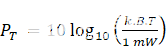
等式 5

哪里：

k = 博尔兹曼常数，1.38064852 x 10-23m2kg s-2 k-1
b = 带宽（赫兹
） T = 以开尔文为单位的温度

由此产生的 NSDT在 25°C （298.15°K） 下计算 1Hz 带宽时为 -173.9 dBm/Hz。

通过简单地比较这三个NSD结果（NSD问14， NSD问16和NSDT），我们看到量化引起的噪声贡献低于本底热噪声;DAC 输出端低 ~2.5dBm/Hz，数字输入端低近 12dBm/Hz。但是，要完成练习，我们将计算 SNR总.

上面的总信噪比方程有三个项，全部以信噪比为单位，是解所必需的。我们只计算了其中之一，我们必须转换热噪声谱密度（NSDT） 信噪比的值T，我们需要信噪比J我们尚未解决的问题。事实上，由于时钟抖动引起的SNR是另一个时间的主题，为了本练习，我们将假设NSDJ和NSDT相等并将该值替换为这两个项。热噪声引起的SNR的计算分为两步。第一步是在奈奎斯特带宽上积分NSD，以获得总噪声功率。一旦我们有了噪声功率，我们就可以根据满量程DAC信号或MAX5868规定的0dBm来计算噪声功率。由此产生的信噪比T14 位 DAC 内核的值为 75.84。实际计算如下所示。

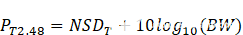
（奈奎斯特的热噪声功率）

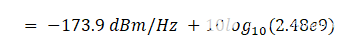
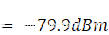
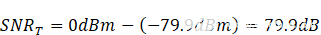
热噪声引起的信噪比

将这些值代入信噪比总等式，我们得出：

 

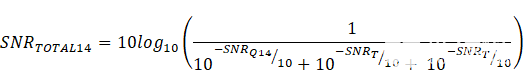
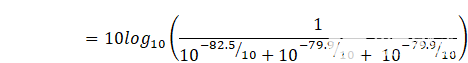
14位分辨率的总理论信噪比

最后，让我们使用625MHz的16位DAC输入接口重新计算总SNR：

 

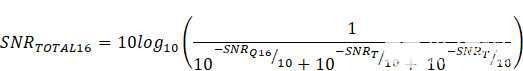
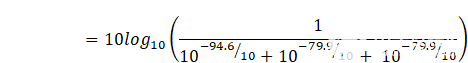
16位分辨率的总理论信噪比

比较结果

量化噪声和SNR的讨论和计算可能很有趣，但它并不能真正解释为什么MAX5868具有16位接口和14位DAC。表1和表2显示了12位至16位分辨率和625MHz和4.915MHz采样速率下的噪声（NSD和SNR）。有趣的事实是，在给定的采样率下，分辨率对总SNR没有影响。

表 1.625MHz数据速率的总信噪比
 

 

分辨率（位）	更新速率（兆赫）	信 噪 比Q （分贝）	国家税务局Q （分贝/赫兹）	信 噪 比总（分贝）
12	6.25E+08	74	-1.59E+02	-91.96
13	6.25E+08	80.02	-1.65E+02	-91.96
14	6.25E+08	86.04	-1.71E+02	-91.96
15	6.25E+08	92.06	-1.77E+02	-91.96
16	6.25E+08	98.08	-1.83E+02	-91.96

 

表 2.4.9152GHz数据速率的总SNR
 

 

分辨率（位）	更新速率（兆赫）	信 噪 比Q （分贝）	国家税务局Q （分贝/赫兹）	信 噪 比总（分贝）
12	4.92E+09	74	-1.68E+02	-83.01
13	4.92E+09	80.02	-1.74E+02	-83.01
14	4.92E+09	86.04	-1.80E+02	-83.01
15	4.92E+09	92.06	-1.86E+02	-83.01
16	4.92E+09	98.08	-1.92E+02	-83.01

 

然而，这些表还显示了由于量化噪声（NSDQ） 直接受分辨率和更新速率的影响，而 SNR总仅受更新速率影响。比较不同采样速率的给定分辨率，很明显，总SNR由热和时钟抖动噪声项决定，而SNR则由SNR主导。Q每增加一位，总SNR提高6dB，无论分辨率如何，总SNR都是平坦的。

结论

优化DAC的性能涉及许多考虑因素。为了确保器件具有足够的分辨率来完成给定的任务，必须在数字域的每个阶段考虑量化噪声，尤其是在采用插值时。虽然12至16位分辨率对总理论SNR没有影响，但采样速率的提高确实将量化噪声分布在更宽的区域，从而有效地降低了本底噪声（NSD）。

审核编辑：郭婷