

光学成像技术:阿贝成像原理和实验解析
光电显示
描述
普遍认为优良显微镜的关键在于减低像差和提高放大倍率,认为显微镜的分辨率是无限的。减低光学镜头像差的一个简单办法是用小的孔径,蔡司公司推出小孔径的显微镜,但结果反而不如以前生产的孔径较大的显微镜。阿贝为了探索个中原因,从理论和试验两个方面进行研究。通过大量的实验,观察显微镜物镜焦平面上的衍射图样,提出显微镜物镜的二次衍射成像理论,并提出:1)显微镜的分辨率存在上限,2)显微镜的分辨率和光的波长、显微镜物镜孔径的关系式。
光学成像是将“物”以其“像”的形式呈现出来,基于几何光学的成像理论,只能给出一些简单的光学成像信息,只有借助于波动光学,才能获得复杂的传输与结构信息。
一、阿贝成像实验原理
阿贝成像原理是1873年,德国科学家阿贝在研究如何提高显微镜分辨本领时提出的;原理指出,成像分为两个步骤,第一步是相干光照明下,物光在透镜后焦面上形成特殊的衍射光分布;第二步是衍射光继续向前传播,复合成像。
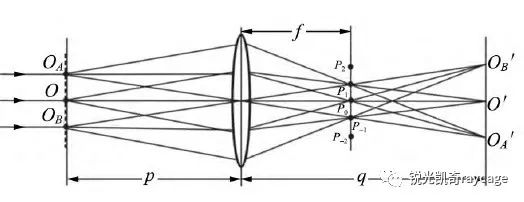
图1 阿贝成像示意图
如图1所示,平行光照明处于O点所在平面上的衍射物,透镜置于衍射物后距离为p处,在透镜后距离为q处放置接收屏,可以得到衍射物的像,成像光路满足:。除此之外,来自不同点的同向光线(同一角度)形成一束平行光汇聚于透镜后焦面上一点(图中各p点)。
汇聚点的振幅是所有同向光线的振幅之和,汇聚点坐标取决于入射平行光的入射方向,由于所有的平行光都是由衍射物衍射产生,所以在光源不变的情况下衍射平行光的方向和强度只取决于衍射物本身的特性和结构。因此衍射物的每一种相同的特性与结构所衍射产生的衍射光经过透镜后,在透镜后焦面上都有一个与之对应的坐标点,也就是说:在透镜后焦面上的每一个点,都对应衍射物的一种结构特性。接下来把这样的每一个点看成一个光源向前传播,并在像面上复合成像,此时如果挡住某些“光源”不让它参与复合过程,所成的像就丢失了某一结构的特定信息。
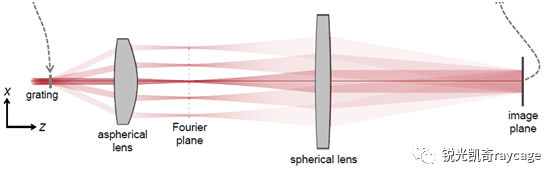
图2 阿贝成像VirtualLab软件仿真示意图
二、二维傅里叶变换
要想比较深刻地理解阿贝成像原理,需要深刻地理解光学傅里叶变换与成像的基本原理。
设二维函数,g(x,y),若其傅里叶变换为:

即:

对G(fx,fy)做傅里叶逆变换可得:

也就是说函数 g(x,y)本身可以由函数 G(fx,fy)做逆傅里叶变换得到,即:

在这里,如果将(2)式用离散求和的方式来表示的话,即:

从上式得到,二维函数可以看作无数个不同频谱信息的周期函数的叠加,反过来 g(x,y)也可以分解为一系列具有不同空间频率的成分。
本实验中光波的衍射传播满足菲涅尔近似条件,这样,当知道上一个面的光场分布时,就可以计算推导出下一个面的光场分布。
现在,再回过头来看阿贝成像理论,第一步是相干光照明下,物光在透镜后焦面形成特殊的衍射光分布,假设物光的光场分布函数是t(x,y),经过透镜后在透镜后焦面上光场分布为T(x,y)=F(t(x,y)),=,这一步是把物光分解成为一系列具有不同空间频率的光场分布,这个面称为傅里叶频谱面;第二步是衍射光继续向前传播,复合成像,这一步就可以看作是不同频谱信息的周期性函数的叠加。
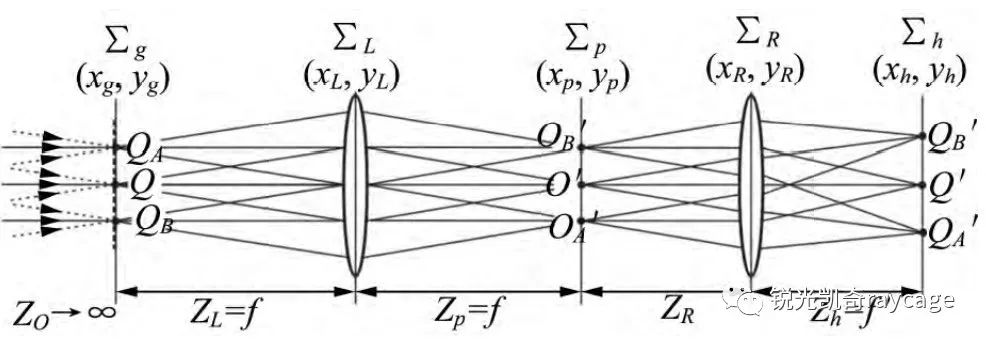
图3 平面波入射标准傅里叶变换
如图3所示,对于平面波入射的标准的傅里叶变换来说将物面置于第一个透镜的前焦面,在后焦面上就可以得到它的频谱信息,频谱面上的光继续向前传播,经过第二个透镜,并在其后焦面上成像,此时如果在频谱面上阻碍一些特定位置的光通过的话,得到的像就会损失某一特定的频谱信息(空间滤波)。
三、阿贝成像实验系统
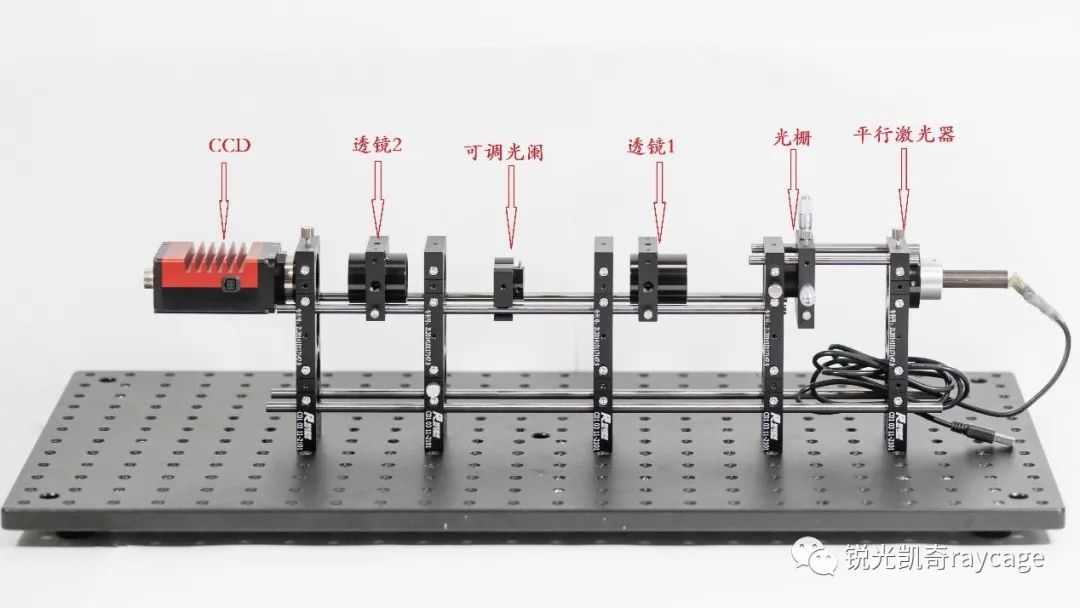
图4 系统示意图
本实验采用650nm平行光照明,样品选用一维光栅,配合两个f=80的透镜和一个置于频谱面上的可调光阑,最后在第二个透镜后焦面上使用CCD采集成像信息,通过调节光阑的大小,控制参与复合成像的频谱信息,从而改变成像效果。
如图5所示为系统频谱面光强分布:
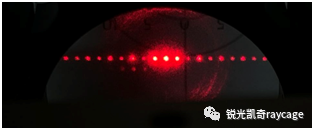
图5 光栅像的频谱面信息

图6
图6是光阑完全打开CCD接收到的像,也就是光栅的像。

图7
图7是只允许+1、0、-1级次通过的像,可以看到条纹之间的小亮点明显减少,也就是高频信息损失了一部分。

图8
图8是只允许0、+1级次通过的像,可以看到,条纹边缘比较模糊,高频信息进一步减少。

图9
当我们只允许0级通过的时候,图像就彻底丢失了高频信息,没有了光栅的周期性分布(如图9所示)。

图10 +1、-1级干涉

图11 +2、+1、-1、-2级干涉
当我们滤除掉0级光过后,低频信息减少,干涉条纹频率增加。其中+-1、+-2级干涉条纹为两个亮条纹之间有一个亮度低的亮条纹。
四、选用器材
600mm*300mm光学平板
三孔固定支撑座
光栅
650nm固体激光器
F=80mm透镜
可调光阑
CCD
[1]张朝晖,刘国超.阿贝成像原理和空间滤波实验[J].物理实验,2017,37(09):23-29.
编辑:黄飞
-
不同医学成像方法电子设计的挑战2019-05-16 0
-
阿贝成像原理和空间滤波2010-07-17 719
-
切伦科夫冷光成像的新型光学成像技术分析2010-07-12 837
-
光学成像与激光散斑成像技术的介绍2017-10-26 1256
-
最创新的近红外二区荧光/生物发光双模式光学成像技术2018-03-15 8313
-
基于深度学习的光学成像算法综述2021-06-16 1305
-
光学成像技术的了解与研究2022-10-10 4951
-
计算光学成像:突破传统光学成像极限2023-01-15 1306
-
基于光学成像的物体三维重建技术研究2023-09-15 906
-
计算光学成像如何突破传统光学成像极限2023-11-17 925
-
浅谈超分辨光学成像2024-03-15 605
-
什么是散射成像技术?2024-08-23 260
-
光学成像的关键技术和工艺2024-11-01 219
-
阿贝数在光学中的应用实例2024-12-20 568
-
阿贝数如何影响光学器件性能2024-12-20 597
全部0条评论

快来发表一下你的评论吧 !

