

KUKA机器人的几何运算符_$介绍
描述
用几何运算符可以以几何方式相加位置。几何相加也被称之为 “Frame 运算”。
在 KRL 中通过冒号 “:” 表示几何运算符。
几何运算符例如适用于以下用途:
移动位置,以根据已更改的工件尺寸对其进行调整
返回策略
示例:
用该指令将工具逆着冲击方向拉回 100 mm,这不取决于机器人现在位于哪个位置上。
LIN $POS_ACT : {x -100, y 0, z 0, a 0, b 0, c 0}
前提是冲击方向在 X 方向上。
$POS_ACT 是结构类型 E6POS 的系统变量,含有当前的笛卡尔机器人位置。
运算的类型 几何运算符可以运算 FRAME 和 POS/E6POS 数据类型。
必须已给分量 X、Y、Z、A、B 和 C 分配了一个值。运算保持分量 S 和 T 不变,因此不必为其分配值。
结果始终有最右侧运算数的数据类型。
| 左侧 | : | 右侧 | 结果 |
| POS | : | POS | POS |
| POS | : | FRAME | FRAME |
| FRAME | : | FRAME | FRAME |
| FRAME | : | POS | POS |
| 左侧 | : | 居中 | : | 右侧 | 结果 |
| POS | : | POS | : | POS | POS |
| POS | : | POS | : | FRAME | FRAME |
| POS | : | FRAME | : | FRAME | FRAME |
| FRAME | : | FRAME | : | POS | POS |
在此,通过之前所述的返回运行示例对其进行了介绍:
| 左运算数 | : | 右运算数 |
| $POS_ACT | : | {x -100, y0, z0, a0, b0, c0} |
| 转至该目标,... | ||
| ... 虽然基于该位置的坐标和姿态。 |
运算数的顺序
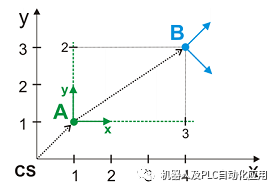
根据运算数的顺序,几何相加的结果不同。这展示了图示中的以下示例。
A = {x 1, y 1, z 0, a 0, b 0, c 0}
B = {x 3, y 2, z 0, a -45, b 0, c 0}
CS = 原点坐标系
可以用 KRL 通过计算运算的结果。这指定了右侧运算数基于左侧运算数坐标系的位置。
顺序 A:B
R = A:B 表示:
A 基于 CS。
B 基于 A。
结果给出 B 基于 CS 的位置:
A点的坐标是基于原点坐标系的
B点的坐标是基于A点的坐标的
R = {x 4, y 3, a -45}
顺序 B:A
R = B:A 表示:
审核编辑:刘清
-
KUKA机器人伺服驱动模块维修2021-09-17 0
-
KUKA重型机器人2015-02-03 0
-
FBD运算符名称2011-04-29 1135
-
条件运算符是什么_条件运算符有哪些2017-11-16 10913
-
单目运算符是什么_单目运算符有哪些2018-02-24 60562
-
C运算符的优先级和结合性详细解决2020-02-22 3238
-
浅析MySQL中的各类运算符2020-05-03 2056
-
python运算符是什么2022-02-21 2386
-
KUKA机器人的几何运算符2022-04-19 5135
-
什么是运算符重载2023-01-20 2494
-
什么是移位运算符2023-02-09 1842
-
Python中运算符介绍2023-03-08 1115
-
KUKA机器人的逻辑运算符2023-07-21 2528
-
C语言运算符的使用方法2023-11-02 1615
-
python中运算符的优先级大小2023-11-29 3412
全部0条评论

快来发表一下你的评论吧 !

