

在数据完整性方面,我们可以只加密数据吗
描述
为了防止有目的地尝试修改数据的对手,我们需要比错误检测/纠正CRC等代码更强大的解决方案。 理想情况下,任何(计算限制的)对手都不应该能够说服我们非法数据来自我们的设备或在我们没有注意到的情况下修改我们的数据。在介绍两种可能的解决方案之前,我们将回顾一些所需的构建块。首先,我们需要了解对称和非对称密码学之间的高级差异。
可以根据私钥的使用方式将不同的加密解决方案分组到类中。当所有用户共享单个私钥时,他们对密钥材料都有相同的知识。由于每个用户在密钥材料上的信息是对称的,因此此类称为对称加密。在另一个类中,每个用户都有一组两个数学上相关的密钥:一个只有他们知道的私钥,以及一个他们与所有人共享的公钥。由于私钥只有用户知道,因此用户之间的信息现在是不对称的。
需要注意的重要区别是,在对称加密中,每个用户都有同一私钥的副本,并且相同的密钥用于两种类型的操作:加密和解密,以及生成和验证签名。在非对称加密中,只有用户知道其私钥,并且只有该私钥可用于解密或签名数据。
需要的另一个工具是一种创建任意大量数据的简短摘要或“指纹”的方法。由于加密操作的计算成本很高,因此在表示(可能更大)数据量的简短摘要上运行它们会更方便。
加密哈希函数采用任意长度的输入并生成固定长度的摘要或“哈希”,该摘要将用作数据的摘要。由于该函数将任意大的输入映射到固定的输出范围,因此肯定会发生冲突。但是,通过使哈希输出的大小足够大,冲突概率可以忽略不计。
哈希函数的另一个重要属性是,即使输入数据中非常小的变化,例如一位翻转,也会导致输出哈希的实质性变化。平均而言,输入数据中的单个位翻转(即使数TB)将导致大约50%的哈希输出位发生变化。这意味着对原始数据的微小更改将导致生成截然不同的摘要或摘要作为哈希函数的输出。再加上碰撞的可能性可以忽略不计,这将作为我们要保护的数据的指纹。
我们可以只加密数据吗?
在尝试保护数据时,我们通常会想到加密。使用密钥加密数据可以使没有密钥的任何人都无法读取加密的密文。那么,我们为什么不对数据进行加密以保护它呢?
加密本身仅提供机密性,不提供真实性或完整性。让我们研究一种常用的加密方法:计数器模式下的 AES。AES 是一种对称分组密码,它使用共享密钥一次加密 16 字节的数据块。分组密码可以在几种不同的模式下运行(组合每个数据块的方法),一种常用的模式是计数器模式。在这种模式下,有一个单调递增的计数器,该计数器被加密以产生伪随机密钥流。为了加密数据,此密钥流与明文输入进行异或运算以生成密文。
密文可以与使用的初始计数器值(初始化向量)一起存储或发送,以便以后使用相同的密钥解密。解密时,将加载初始计数器值,并使用相同的密钥再次加密以生成相同的密钥流。此密钥流与密文进行 XOR 运算,以取消加密操作并恢复明文。
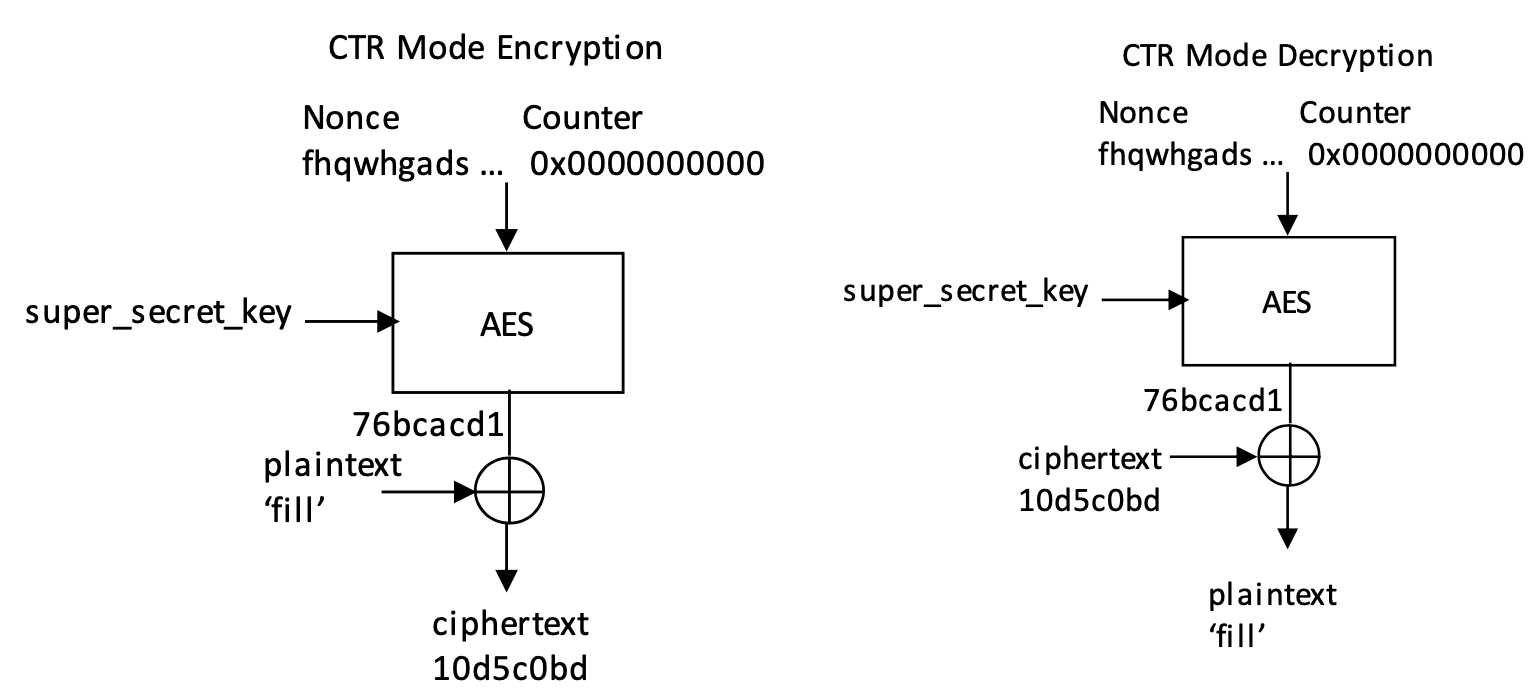
如果对密文的修改也以可预测的方式修改基础明文,则密文称为可延展性。计数器模式下的分组密码(以及其他流密码)具有微不足道的延展性。翻转密文中的单个位将在解密时翻转明文中的相同位,而不会更改任何其他位。这意味着攻击者可以轻松修改加密数据并预测此更改对解密数据的影响,即使他们不知道密钥或基础明文消息也是如此。
考虑有两个系统通过无线发送和接收在计数器模式下使用 AES 加密的消息进行通信的情况。攻击者可能能够拦截通信,即使他们可能无法解密消息,他们也知道他们可以翻转密文中的位以翻转明文中的相同位。在某些情况下,可能很容易猜到明文可能是什么。这些类型的机器对机器通信通常具有结构化和可预测的格式。攻击者可能已经获得了与之相关的文档,或者可能只是能够猜测它或对其进行逆向工程。
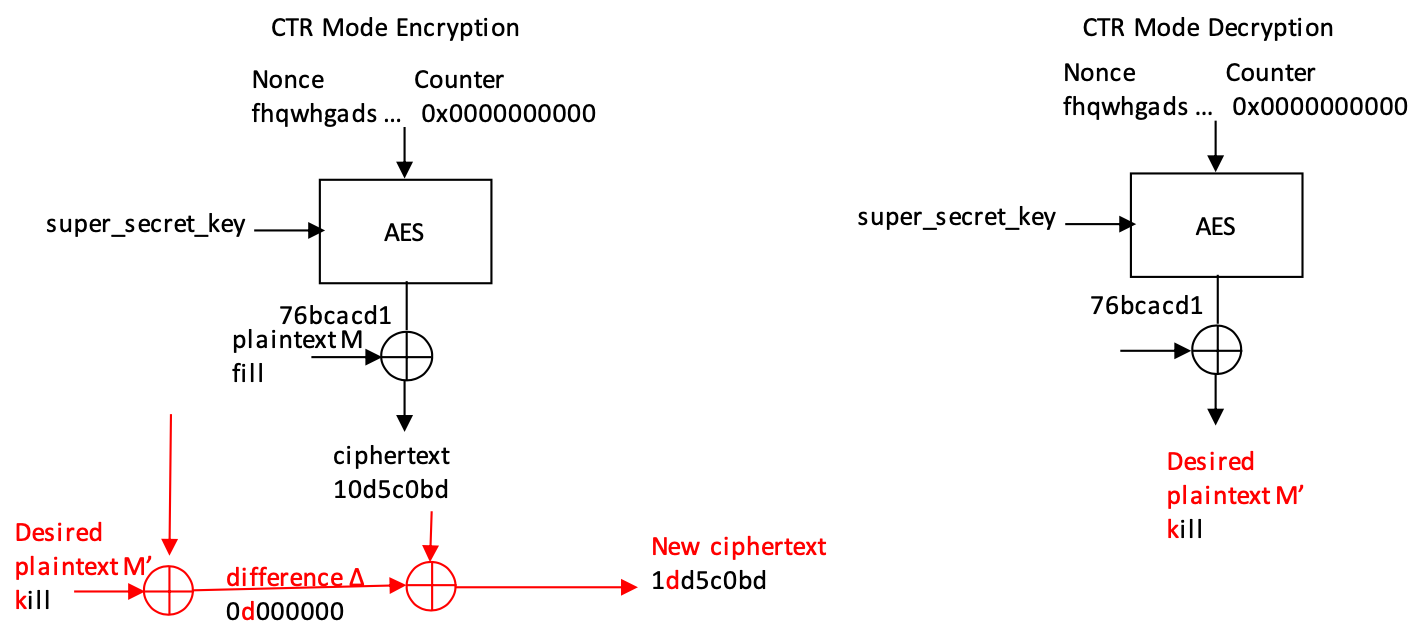
在我们的示例中,攻击者想要中断运营中心的订单。攻击者知道交换消息的格式(通过阅读用户手册),处理订单的命令是“fill”,删除订单的命令是“kill”。在上图中,我们可以看到执行订单的命令已正确加密和解密。让我们看看攻击者如何在不被发现的情况下更改此命令,即使消息将被加密!
攻击者知道明文消息中“fill”命令的位置,并希望恶意将命令更改为“kill”,以导致订单被取消,而不是履行。
首先,攻击者计算消息 M = “填充” 和 M' = “kill” 之间的差∆。通过∆包含明文消息“fill”的密文块进行异或运算,解密消息中的字符“f”将更改为“k”!
由于仅加密并不能阻止这些数据被修改,我们可以通过加密消息及其CRC来保护其完整性吗?攻击者不会知道CRC的值,如果他们修改密文,CRC应该检测到修改,对吧?正如我们在上一节中看到的,加密可以是可延展的,不幸的是,加密的CRC也可以。
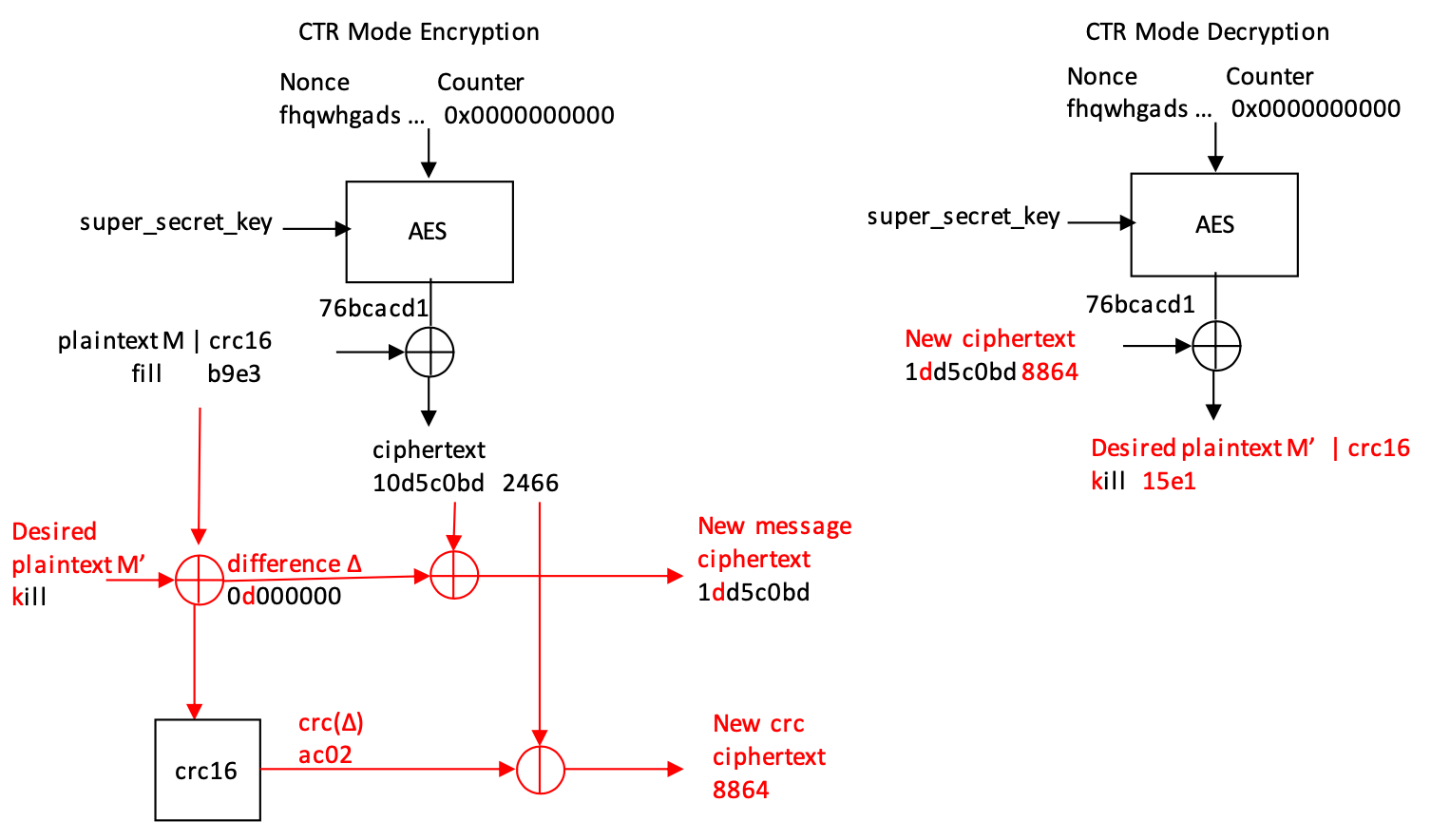
假设我们有一个加密的消息M,它也包含该消息上的加密CRC,并且我们知道密文中与加密CRC相对应的位置。如果我们想将消息 M 修改为新消息 M',我们还需要修改 CRC。
设 ∆ = M Å M' 是原始消息 M 和新消息 M' 之间的差值。这是两个异或一起,或者已经改变的位(如果∆的每个位是我们翻转的消息中的位,则为 1)。原始 CRC 与新计算的 M' 上的 CRC 不匹配。我们需要修改 CRC,使其在新消息 M' 上有效。
由于CRC是一个线性函数,CRC(M') = CRC(M) Å CRC(∆)。换句话说,为了获得一个新的有效CRC,我们计算∆上的CRC函数(我们已经更改的位的CRC),并使用CRC对这个值进行XOR。正如我们之前看到的,我们甚至可以在密文上完成所有这些操作,甚至不知道消息的真实值或 CRC 的值,我们可以使用有效的 CRC 将消息更改为我们想要的任何内容!
这种弱点不仅仅是理论上的。它存在于有线等效保密 (WEP) 算法中,该算法允许以类似的方式修改 WEP 流量。
因此,仅仅加密数据本身并不能保护它不被修改,加密的CRC也不能。如果明文CRC,加密数据或加密数据及其CRC不能保护我们的数据免受故意修改,那又有什么作用呢?
审核编辑:郭婷
-
信号完整性分析与设计2009-09-12 0
-
信号完整性与电源完整性的仿真分析与设计2015-01-07 0
-
我们为什么重视系统化信号完整性设计方法(于博士信号完整性)2017-06-23 0
-
数据加密技术主要应用在哪些方面2021-02-25 0
-
如何保证STM32串口接收数据的完整性?2021-12-09 0
-
什么是电源和信号完整性?2021-12-30 0
-
怎样学好“信号完整性”?2017-08-29 20671
-
保持 EMIF 通道信号完整性的数据测量2018-06-20 8414
-
数据完整性问题的解决办法——校验和2020-08-31 5845
-
基于群签名算法的云共享数据完整性审计2021-05-29 624
-
信号完整性与电源完整性的仿真2021-09-29 1327
-
ADS在信号完整性和电源完整性仿真方面的应用2022-08-30 6768
-
数据完整性:验证数据未被更改2023-02-07 922
-
什么是信号完整性2024-05-28 1213
-
信号完整性与电源完整性-电源完整性分析2024-08-12 1049
全部0条评论

快来发表一下你的评论吧 !

