

机器视觉学习—边缘检测
描述
前言
边缘检测是图像处理和计算机视觉中,尤其是特征提取中的一个研究领域。有许多方法用于边缘检测,它们的绝大部分可以划分为两类:
基于一阶导数
首先计算边缘强度, 通常用一阶导数表示, 例如梯度模,然后,用计算估计边缘的局部方向, 通常采用梯度的方向,并利用此方向找到局部梯度模的最大值。
即:图像一阶导数中的最大和最小值来检测边界,通常是将边界定位在梯度最大的方向。
一阶:Roberts Cross算子,Prewitt算子,Sobel算子, Kirsch算子,罗盘算子;
基于 零穿越/零交叉 的一类:二阶导数
基于零穿越的方法通过寻找图像二阶导数零穿越来寻找边界,通常是Laplacian过零点或者非线性差分表示的过零点。
基于二阶导数:Marr-Hildreth,在梯度方向的二阶导数过零点,Canny算子,Laplacian算子。
一、边缘检测
为什么要进行边缘检测呢?因为这是稳定的视觉特征,是人类经验的结果。边缘检测的目的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。主要包括:
深度上的不连续(物体处在不同的物平面上);
表面方向不连续(如正方体的不同的两个面)
物质属性变化(会导致光的反射系数不同)
场景照明变化(阴影)
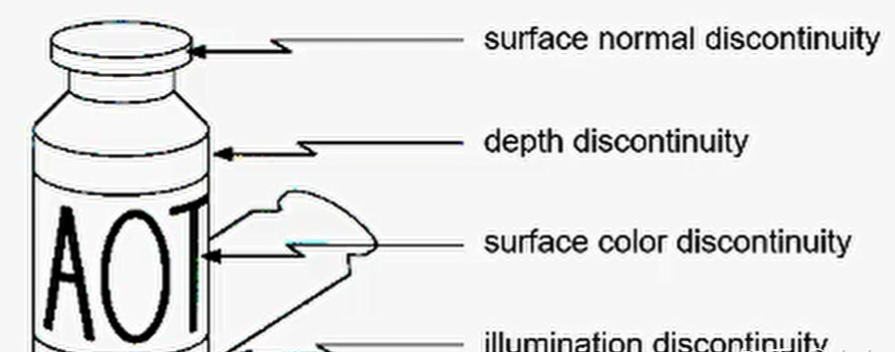
那么,对于下面这张图像进行边缘检测时,沿着这条红色的水平线,得到其每个像素点上的强度(也就是灰度值),由此可知边缘就是在像素值发生突变的地方。那么如果从一个信号中找到突变的地方呢?
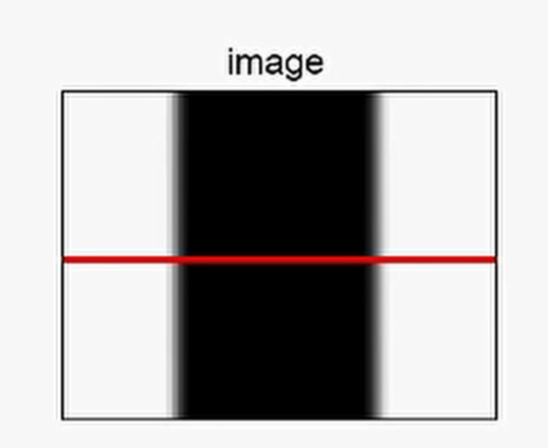
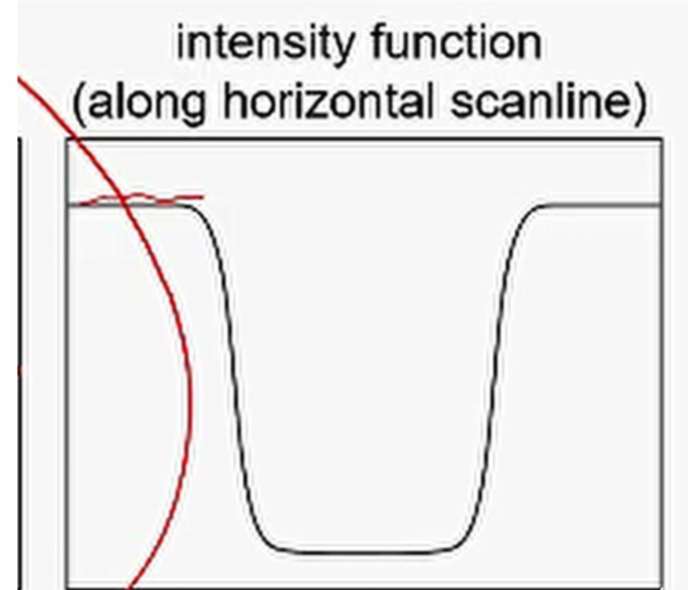
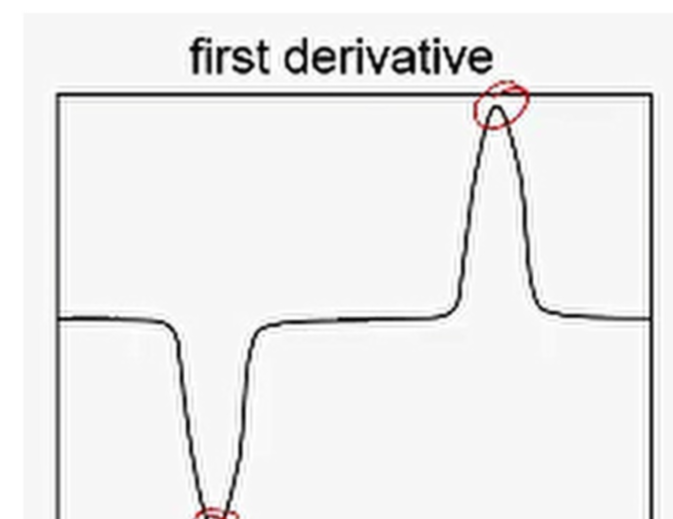
显然,根据数学知识,对信号曲线进行求一阶导数,对于边缘来说,并不需要关注方向,只需要关注极值即可,所以可以通过求导得到边缘所在位置。
由此将这跟红色的水平线从上至下滑动即可得到整个图像的竖直方向上的边缘。
对于一个二元函数f(x,y) ,响应的的求导公式:
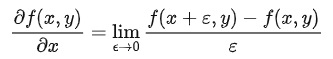
在图像处理过程中,对于像素值的位置的最小单位是 1 px,因此令 ε=1 ,使用这种近似来作为点前位置的导数,则有:
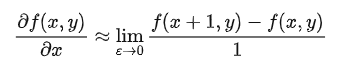
其实由这个公式可以看出,就是右面一个像素减去左面一个像素,作为当前位置的导数,这样简化之后其实就可以把这个过程使用卷积代替,即卷积核为:这就是检测竖直方向上边缘的卷积核。同理也可以得到水平方向上边缘的卷积核。
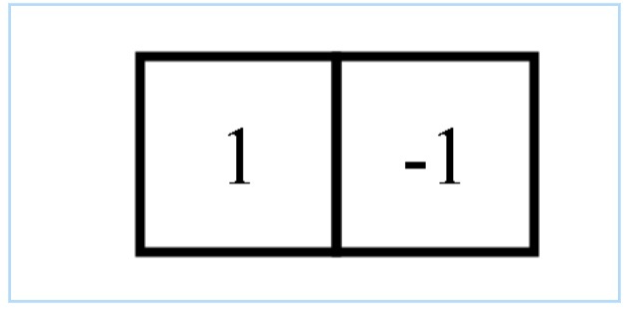
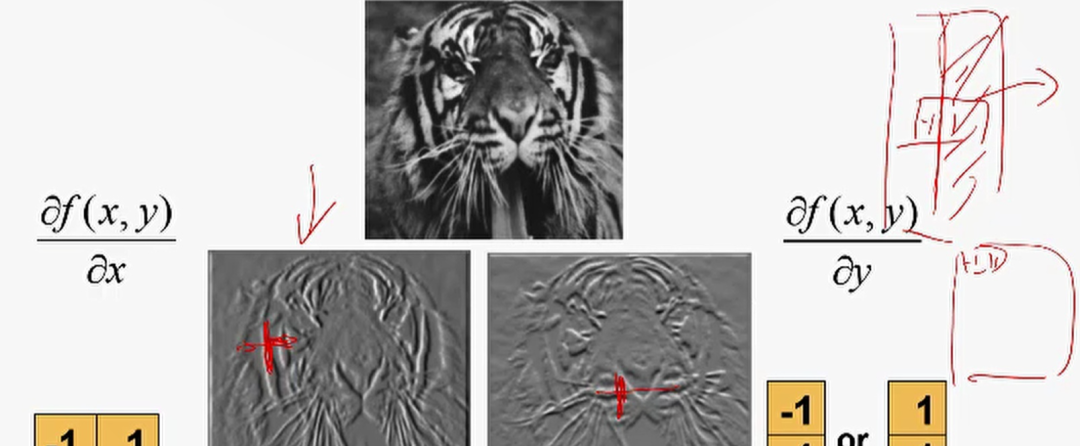
那么接下来举个例子,下面这两个边缘检测结果哪个是水平方向卷积核检测到的?
哪个是竖直方向卷积核检测到的?因为只有水平卷积核检测的是左右差异较大的像素值,自然而然连成线之后就是竖直方向的线条。
接下来,解释一下梯度(一维叫导数,高维叫梯度),对于一副图像的一个像素点
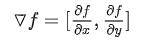


这个幅值越大说面这点附近像素值变化越剧烈,就越有可能是边缘。
其实梯度对于一副图像来说就是图像变化剧烈的方向。而且梯度方向与边缘是垂直的。
二、边缘检测流程
由于在实际应用过程中信号的采集往往伴随着噪声的出现,假设有下面这么一个一维信号,很显然边缘就在突变的地方。但是由于真实点附近存在噪声,如果直接使用边缘滤波器(边缘卷积)得到的结果会是什么样?
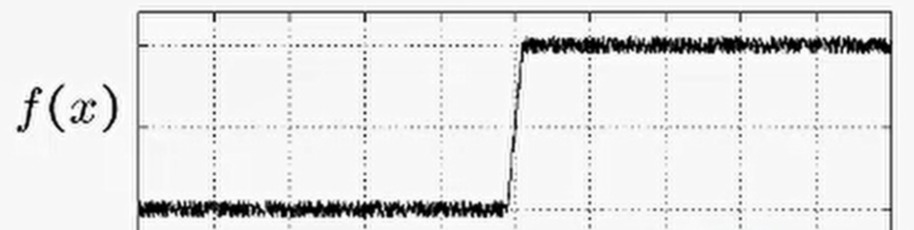
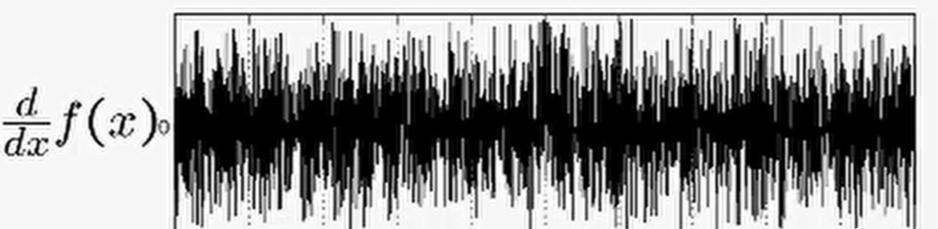
显然,通过边缘检测器之后得到导数(梯度)是无法确定极大值极小值的,因此无法判断边缘位置。所以,往往在进行边缘检测前首先要进行滤波。
这是因为边缘检测算子主要是基于图像强度的一阶导数和二阶导数,但是通常情况下导数对噪声十分敏感,因此必须使用滤波器来进行平滑噪声。
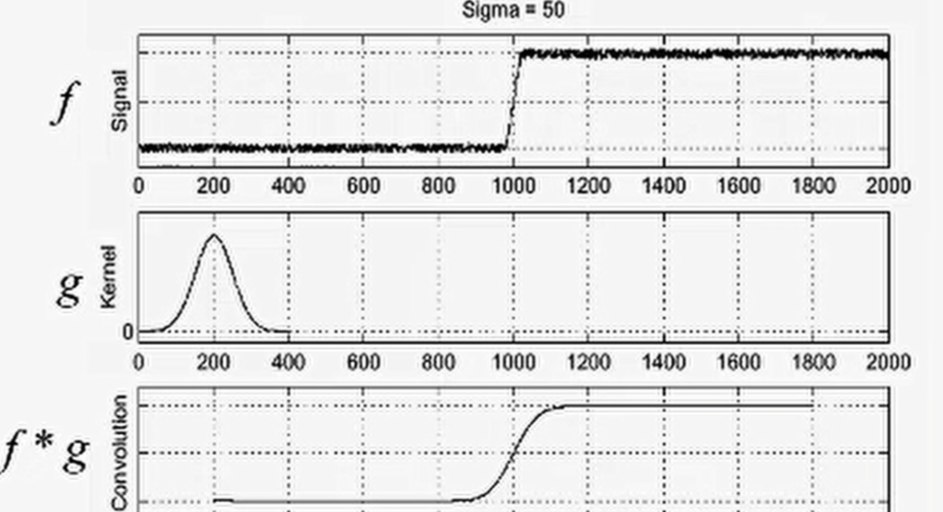
因此对于一维图像f使用高斯卷积核 g进行滤波,通过将f*g(卷积)得到的结果可以看出,最左边和最右面为什么没了呢?这就是因为卷积过程中如果不对边界补充的话,卷积结果相比原来图像会小一圈。
经过高斯卷积之后的图像就相对平滑很多,在这个基础上再进行边缘检测,得到结果如下。很显然求极值就十分简单了。

因此,我们在对图像进行边缘检测前首先用高斯卷积对图像进行平滑就是了,因为我们也无法确定图像是否包含噪声。
虽然上面这个过程实现了边缘检测,但是在这个过程中使用了两次卷积,首先是滤波过程的卷积,然后是求导过程的卷积,显然卷积是十分耗时的,那么能否使用一次卷积完成这个操作呢?
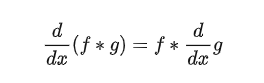
这个公式成立是因此卷积是满足交换律,结合律和分配率的。所以使用右面的公式,先对高斯卷积核进行求导,这个模板一般比较小,求导也相对简单,然后再进行卷积。这样就能加速运算过程了。
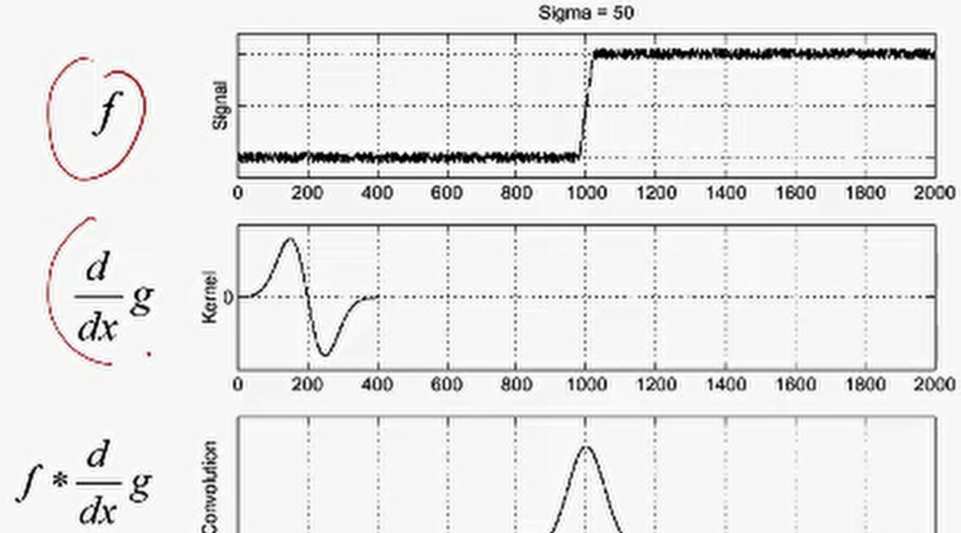
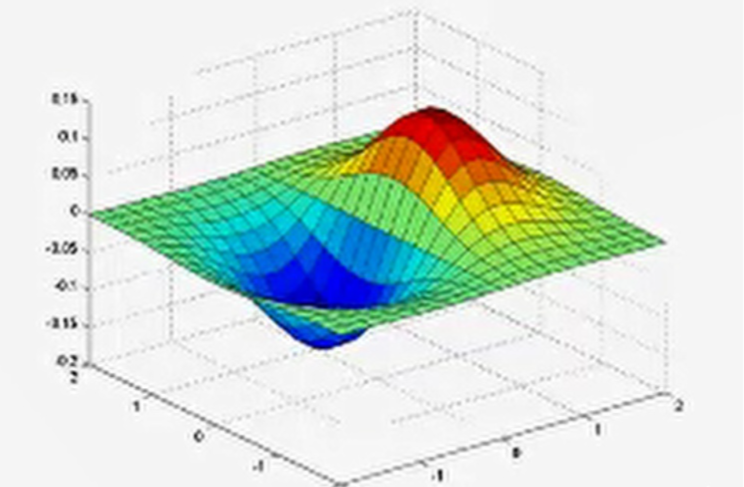
虽然,使用平滑对图像进行去噪,但是它也会模糊图像,因此我们可以考虑在不同的scale下进行边缘检测。
也就是选择响应的窗宽和标准差即可对图像进行平滑并边缘检测,由于窗宽一般默认经验值3σ,因此只需要指定参数σ即可执行这两个过程。所以可以考虑使用不用的σ在不同的scale下进行边缘检测。
因此,接下来对比重新认识一下高斯卷积核与高斯一阶导数核的区别:
高斯卷积核(smoothing filters):高斯卷积实际上是滤除高频信号,是低通滤波器,滤波器模板中的数值没有负数,而且这些值相加和为1。

高斯一阶导数核(derivative filters):滤波器模板中的数值一定有负数,而且这些相加为0。

总结一下,对于一副图像进行边缘检测的流程
滤波
增强,增强算法可以将图像灰度点邻阈强度值有显著变化的点凸显出来。
边缘检测,经过增强的图像,往往邻域中有很多点的梯度值比较大,而在特定应用中,这些点并不是要找的边缘点,所以应该采用某些方法对这些点进行取舍。实际工程中,常用的方法是通过阈值化的方法进行检测。
三、Canny边缘检测

对于这样一张图像进行边缘检测时,首先第一步,对图像进行滤波处理,然后计算两个方向的梯度,先计算每个像素点的梯度,然后计算幅值,得到下面这张图像。

在进行梯度计算时,梯度较大的地方可能是边缘也有可能是噪声,虽然已经进行过一次平滑滤波,但是仍然还会有一些高强度的噪声无法滤除,因此在这里选择使用阈值对其进行第二次过滤,去除一些梯度相对较小的点。
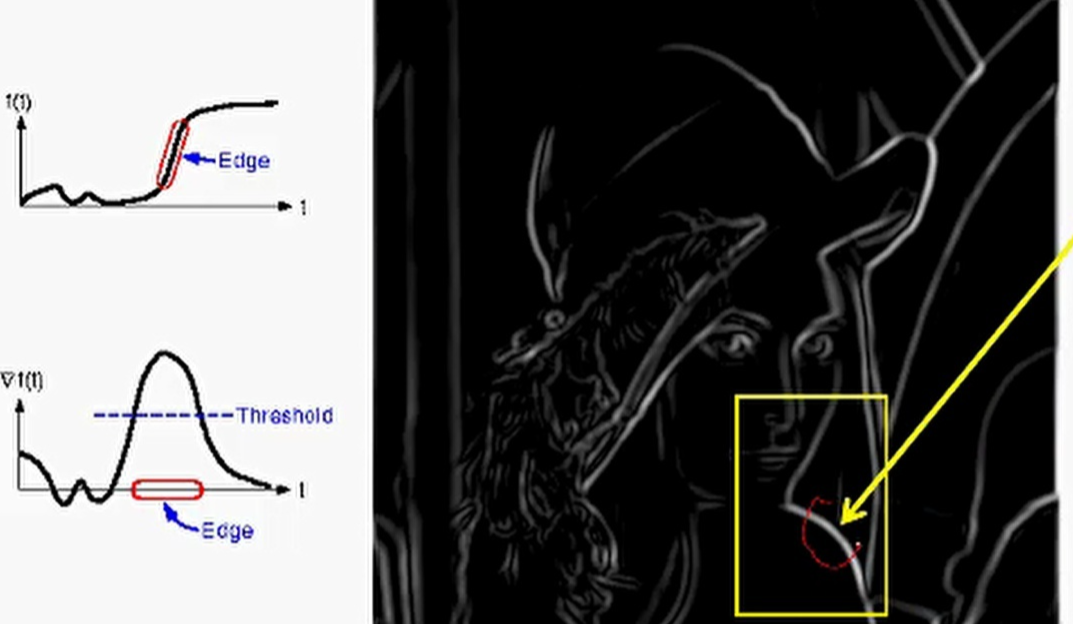
然而经过阈值处理后,还是会有一些小问题,就是图像中的边缘会很宽,这是由于图像中的边缘像素值都是缓慢变化的,不会是一个垂直的突变,即使原始图像中的边缘是一个垂直的突变,经过高斯平滑之后它就会变得不那么垂直了,所以这就是为什么边会那么宽。那如何解决呢?
接下来就介绍了一个著名的算法:NMS非极大值抑制。它的一个主要思想就是,首先确定边上的一个点,然后沿着边的梯度方向比较跟相邻点的梯度进行比较,也即是右图中的q和Ρ,γ进行比较。如果 q 最大则保留,如果不是则舍去。

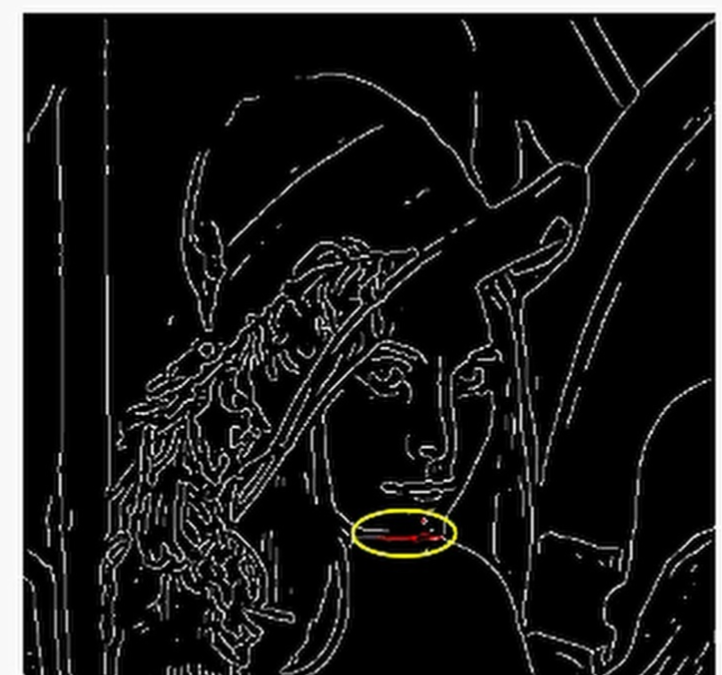
经过抑制以后:显然这就细化了很多,但是也会存在一定的问题,比如脖子下面的边缘消失了,出现了断断续续的情况,出现这种情况的原因是什么呢?
这是因为设置的阈值太高了,导致这部分梯度被滤除掉了,但是如果阈值设置的较低又会出现很多“假边”,因此这里需要对刚刚设置阈值过滤这一步进行改进。
改进的思路:就是使用双阈值法,首先使用一个较高的阈值去将那些确定度较高的边检测出来,称为“强边”,然后再使用一个较小的阈值显露更多的边,称为“弱边”,此时选择保留那些跟强边有连接关系的边。这个想法就很巧妙。

左边是高阈值,中间是低阈值,右边是双阈值
关于Canny边缘检测是有严格意义上的数学推导的,这个后续补充一下!
审核编辑 :李倩
-
#硬声创作季 机器视觉技术与应用:基于微分的边缘检测Mr_haohao 2022-10-26
-
#硬声创作季 机器视觉技术与应用:canny边缘检测算子Mr_haohao 2022-10-26
-
机器视觉 --检测图像边缘小程序2015-08-23 0
-
机器视觉算法与应用(双语版)2016-06-29 0
-
机器视觉检测设备的优势2019-10-14 0
-
深圳机器视觉检测项目包括哪些?2020-11-11 0
-
高性能的机器学习让边缘计算更给力2021-10-15 0
-
基于机器视觉定位技术之产品边缘轮廓检测2021-04-14 1991
-
如何在OpenCV中使用基于深度学习的边缘检测2021-04-18 1843
-
探究机器视觉定位技术之产品边缘轮廓检测2021-04-19 1869
-
OpenCV使用深度学习做边缘检测的流程2021-05-08 2266
-
什么是边缘学习2022-10-20 2679
-
面向工业边缘的机器学习和智能视觉2023-05-25 785
-
机器视觉检测平台2023-06-29 822
-
深度学习在工业机器视觉检测中的应用2024-07-08 1045
全部0条评论

快来发表一下你的评论吧 !

