

RF设计基础知识:VSWR、回波损耗和失配损耗
RF/无线
描述
当电波在其中传播时遇到介质的阻抗变化时会反射。当我们打算将功率从信号链中的一个块传输到下一个块时,这些反射是非常不受欢迎的。
在本文中,我们将了解两个参数,即 VSWR 和回波损耗,这使我们能够表征RF 设计中的波反射。我们还将讨论参数化波反射对功率传输的影响的“失配损耗”规范。
计算 VSWR 公式
对于短路或开路的传输线,会发生全反射,入射波和反射波的干扰会在传输线上产生驻波。例如,请考虑图 1 中所示的图表。
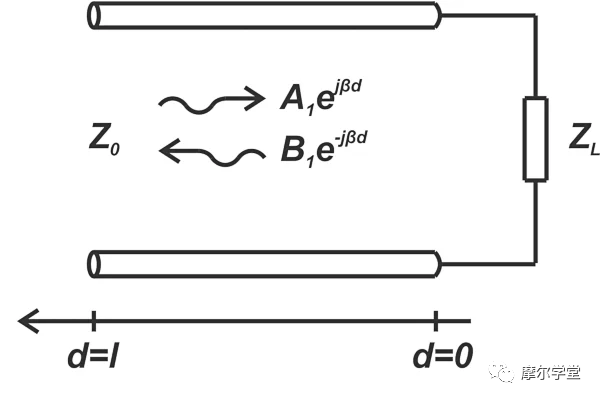
图 1. 示例图。
对于正弦输入,稳态响应也是正弦的。在 d = 0.2 米的长度和短路负载 (Z L = 0) 的情况下,36 个不同时刻沿线的电压波形如图 2 所示。
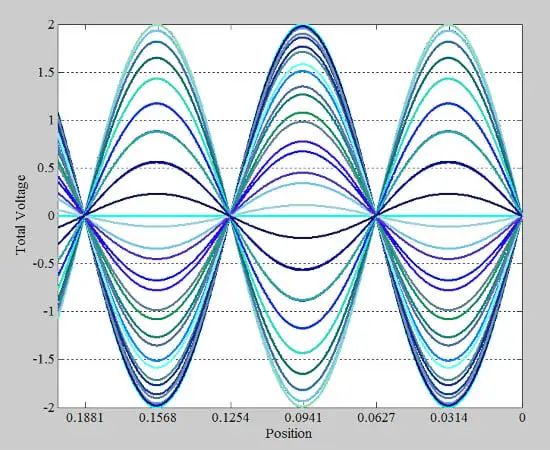
图 2. 36 个不同实例的电压波形。
上面的曲线让您了解电压波的幅度如何沿线变化。上图的包络线最好地显示了这种幅度变化,如下面的图 3 所示。
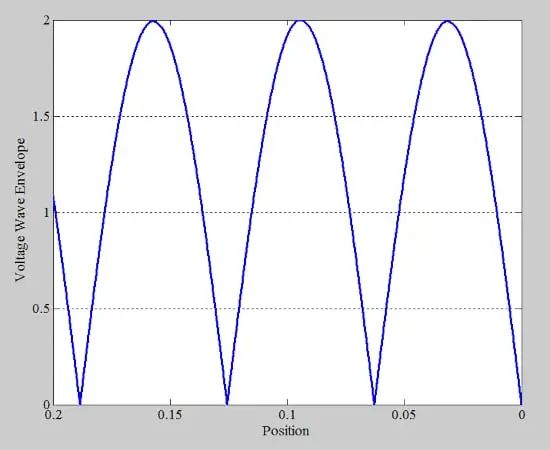
图 3. 振幅变化图。
请注意,包络线的最小值为零伏。我们可以对任意负载重复相同的过程,比如 Γ = 0.5 的负载。这种情况下 36 个不同时刻的电压波形图如图 4 所示。
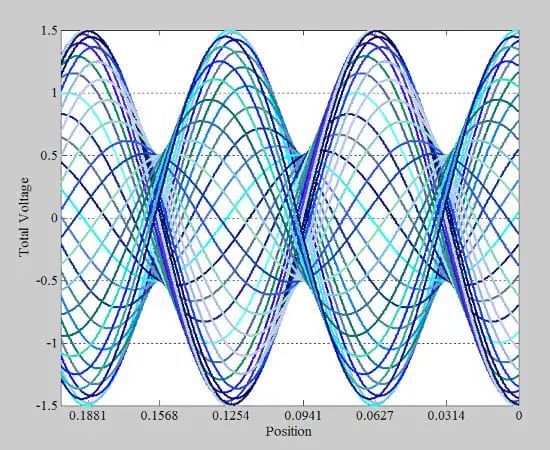
图 4.另一个示例图显示了 36 个实例的电压波形。
这些曲线的包络如图 5 所示。
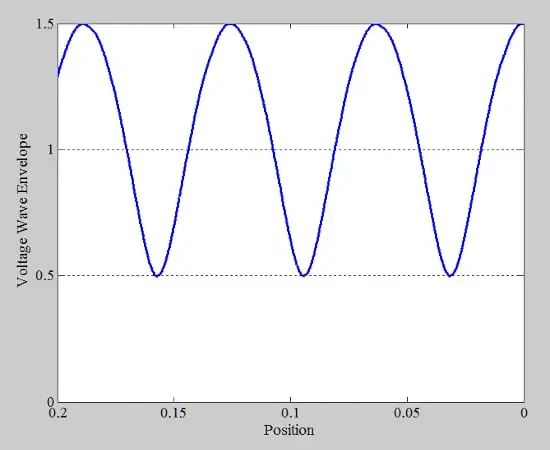
图 5. 示例电压波包络与位置图。
上面的讨论表明,当发生全反射时,包络的最小值为零伏 V min = 0(图 3)。然而,对于部分反射,V min 更接近峰值V max。在没有反射的理想情况下,V max 实际上等于 V min。因此,V max 与 V min之比(称为 VSWR)与阻抗不连续处发生的反射量有关。在数学语言中,VSWR 定义为:
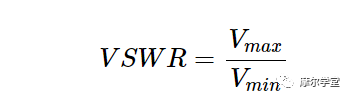
等式 1。
全反射时,驻波比为无穷大;对于匹配负载,VSWR 为 1;对于其他情况,VSWR 介于这两个极值之间。例如,对于图 5 中的包络波形,VSWR 为:
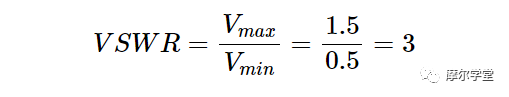
可以很容易地看出,VSWR 与负载反射系数Γ 的关系由下式表示:
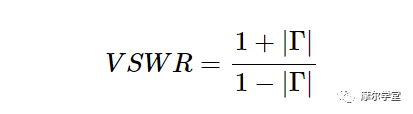
等式 2。
这个等式允许我们测量 VSWR 并使用该信息来确定反射系数的大小。
附带说明一下,VSWR 参数可能已经失去了它曾经具有的重要性。今天的高性能定向耦合器可以物理分离入射波和反射波,使我们能够准确地测量反射系数。
在传输线测量的早期,这些高性能定向耦合器是不可用的,公式 2 是测量 Γ 幅度的简单解决方案。为此,工程师只需通过一种称为槽线的设备测量线路沿线的最小和最大电压即可。考虑到当今高性能测量设备的可用性,VSWR 有时被认为是几十年前遗留下来的参数。然而,RF 工程师需要完全理解 VSWR 概念,因为它仍然通常在数据表中指定。
射频回波损耗
考虑图 6 中的图表,其中传输线连接到 RF 组件的输入。入射功率为 P i, “观察”RF 组件输入的反射系数为 Γ。
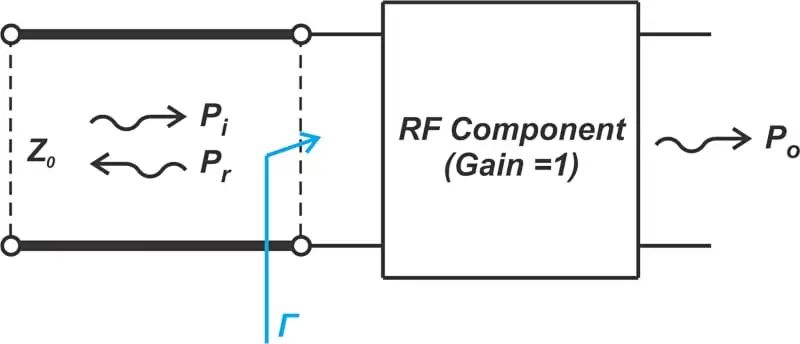
图 6. 显示 RF 组件和传输线的图表。
在这里,我们感兴趣的是表征有多少入射功率从 RF 组件 (P r ) 反射。而反射系数Γ是反射电压与入射电压之比,|2|C|2 表示反射功率与入射功率之比:
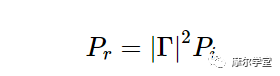
等式 3。
用分贝表示上述等式产生:
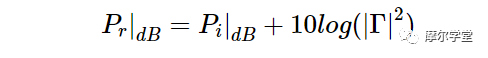
等式 4。
例如,如果
|Γ|2=0.1,我们得到:
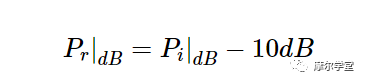
这意味着反射功率比入射功率低 10 dB。在这种情况下,我们可以说返回的入射信号部分经历了 -10 dB 的增益,或者等效地,损失了 +10 dB。换句话说,本例中的“回波损耗”为 10 dB。
或者,回波损耗参数通常用于表示等式 3 和 4。但是,这个参数的名称起初可能有点令人困惑。回波损耗指定入射信号在从阻抗不连续性返回或反射时经历的损耗。
请注意,对于无源威廉希尔官方网站 ,Γ 介于 0 和 1 之间,因此,返回的信号经历衰减或损失而不是增益。回波损耗,通常用 RL 表示,由下式给出:
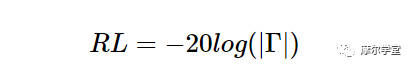
等式 6
例如,如果系统中的回波损耗指定为 40 dB,您会立即知道反射功率比入射功率低 40 dB。因此,较大的回波损耗对应于负载与线路特性阻抗之间更好的匹配。
Γ、VSWR 和回波损耗这三个参数都是指定负载与传输线匹配程度的不同方式。然而,与具有幅度和相位信息的 Γ 不同,VSWR 和回波损耗仅提供幅度而没有相位信息。
失配损失
让我们再检查一次图 6 中的配置。除了反射功率之外,我们还对表征阻抗不匹配对传输到输出 P o的功率量的影响感兴趣。首先,假设 RF 组件的功率增益为单位 (G = 1)。换句话说,传送到射频组件输入端的功率相同,出现在其输出端。由于阻抗不匹配会导致一些反射功率,它会降低传递到 RF 组件的功率。当 G = 1 时,输出功率 P o 等于入射功率与反射功率之差:
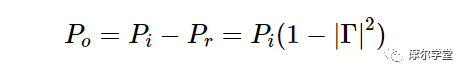
用分贝表示上述等式导致:
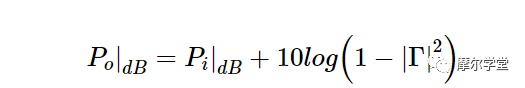
继续示例值
0.1|C|2=0.1,上面的等式产生:
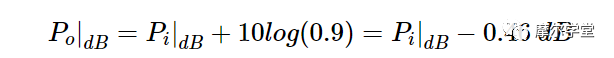
这意味着输出功率比入射功率低 0.46 dB。换句话说,信号经历了 -0.46 dB 的增益,或者等效地,损失了 +0.46 dB。这种功率损失被称为“失配损失”,因为它仅源于阻抗失配。失配损耗参数告诉我们通过提供完美的阻抗匹配可以获得多少增益改进。在上面的示例中,可获得的增益改进为 0.46 dB。基于上述讨论,由 ML 表示的失配损失由以下等式给出:
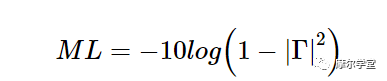
等式 7。
从上面的解释中可以清楚地看出,小的失配损耗是需要的,并且对应于负载和线路之间更好的匹配。
两个端口不匹配时的不匹配损失
在图 6 中,我们隐含地假设信号源(未显示)的阻抗与线路特性阻抗匹配。如果不是这种情况,P r 将重新反射源端的不连续性并影响入射波 P i。例如,当我们通过传输线将源连接到负载时(图 7(a))以及两个级联设备之间的接口(图 7(b)),就会遇到这种情况。
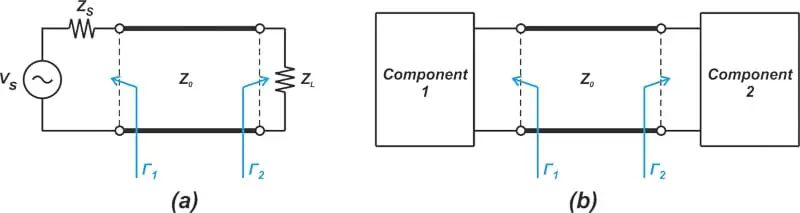
图 7. 源通过传输线 (a) 和两个级联设备之间的接口 (b) 连接到负载的示例图。
在这种情况下,失配损耗(以线性项而不是分贝表示)由公式 8 给出。
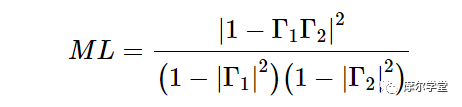
等式 8。
上式指定了由于波反射而在输入和输出端口之间来回反弹的输入功率部分。您可以在G. Gonzalez 的“微波晶体管放大器”第 2 章中找到该方程式的推导。例如,假设图7(a)中的Γ 1 和Γ 2 分别为0.1和0.2。在这种情况下,我们有 ML = 1.011 的不匹配损失。以 dB 表示,由于两个阻抗不连续,我们有 0.05 dB 的损耗。
请注意,Γ 具有幅度和相位信息,相位角会影响公式 8 生成的 ML 值。让我们重复上述示例,其中 Γ 1 = 0.1 和 Γ 2 = -0.2。在这种情况下,ML 计算为 1.095 或 0.39 dB。
失配不确定度
上述示例突出了 RF 应用中的严峻挑战。由于等式 8 中的失配损耗取决于反射系数的相位角,并且注意到在许多实际情况下,只有反射系数的大小是已知的,因此对于实际从输入传输到输出的功率有多少存在一些不确定性. 例如,知道 |Γ 1 | = 0.1 和 |Γ 2 | = 0.2,失配损耗介于 0.05 dB 和 0.39 dB 之间。由这些上限和下限指定的范围称为失配不确定性,我们将在本系列的下一篇文章中更详细地讨论它。
审核编辑:汤梓红
-
一文看懂RF领域中的驻波比和回波损耗2025-03-28 0
-
射频衰减器改善信号发生器或频谱分析仪的失配损耗2017-11-07 0
-
用于测量RF功率和回波损耗的集成双向桥2018-10-23 0
-
Keysight 8161X回波损耗模块的回波损耗解决方案2019-06-12 0
-
宽带RF功率和回波损耗测量2018-06-04 4519
-
回波损耗越大越好吗2020-01-06 17220
-
回波损耗是什么意思_回波损耗为什么不通过2020-01-06 17004
-
什么是插入损耗,回波损耗又是什么2020-11-05 30049
-
插入损耗和回波损耗是什么2020-12-25 4393
-
免校准回波损耗测量2023-01-06 1982
-
了解电压驻波比VSWR、回波损耗和失配损耗2023-02-09 4263
-
失配损耗对射频功率测量和级联放大器增益的影响是什么2023-02-19 2323
-
通过衰减器和统计模型实现失配损耗和失配不确定性2023-02-27 1915
-
怎么解决失配损耗对有损线路的影响?2023-10-30 640
-
插入损耗是什么?回波损耗是什么?影响插入损耗和回波损耗的因素2023-12-27 3466
全部0条评论

快来发表一下你的评论吧 !

