

三极管的基本特性、特征方程及工作状态
模拟技术
描述
晶体管分为三极管和场效应管两种,这里我们先说三极管,场效应管的内容我之前发过不少,但是还不全,后面我会慢慢补上。
1、三极管的基本特性
三极管分为NPN型和PNP型两种。 这里我不会讲它的物理结构这个微观层面的东西,只讲具体在威廉希尔官方网站 中我们怎么应用,怎么理解,怎么在大脑中构建这个模型。
如下图,三极管的三个引脚分别是基极(Base),发射极(Emitter),集电极(Collector)。
等效模型:BE直接就是一个二极管,CE直接等效为一个可调电阻,阻值可以从若干欧到无穷大(开路)。 (记住这个等效模型可以解决90%的问题,非常重要)
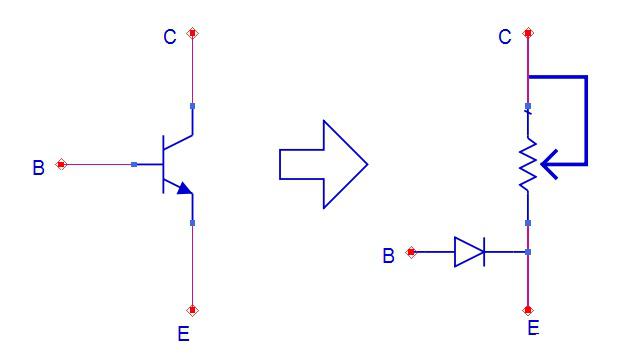
NPN型三极管等效模型
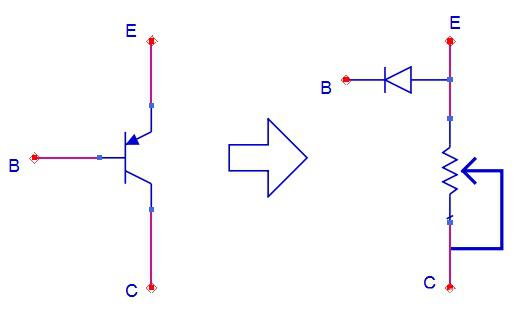
PNP型三极管等效模型
2、三极管的特征方程
ic = beta * ib,为什么叫特征方程呢? 所为特征就是本质的意思,一个三极管生产出来了,ic和ib就是这个关系,beta是个常数,是三极管自身的放大倍数,取决于生产工艺数值在几十到几百之间。 理解三极管就要从这个beta开始。
对于NPN型三极管,ib从B→E,ic从C→E。
对于PNP型三极管,ib从E→B,ic从E→C。
三极管有三个工作状态,饱和区,截止区和放大区,一个三极管固定了怎么会有三个工作状态呢? 阻容感器件可没这么多说法,很难理解,别忘了,等效模型中有一个量是变化的--可调电阻。 就是根据这个可调电阻来划分三极管的工作状态。
3、三极管的工作状态
三极管只能依靠改变CE直接的可调电阻R_ce来实现ic=beta * ib。
① 饱和区,如果R_ce降低到最小值,都实现不了ic=beta * ib,称为“饱和”。 (此时,R_ce为最小值,CE近似短路,但不满足ic=beta*ib)
② 截止区,如果R_ce增大到最大值,都实现不了ic=beta * ib,称为“截止”。 (此时,R_ce为最大值,CE近似开路,但不满足ic=beta*ib)
③ 放大区,如果在R_ce可调范围内能够ic=beta * ib,称为“放大”。
举个例子:
① VCC=10V,问三极管工作在哪个区?
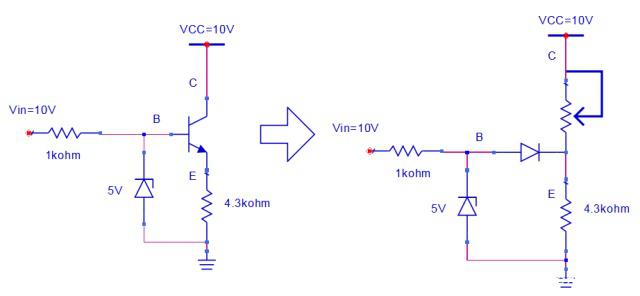
左边原理图,右边等效威廉希尔官方网站 图
答:由于有5V稳压管存在,B为5V,减去二极管管压降0.7V,得到E为4.3V,所以E极电流为1mA,假设工作在放大区ic=beta * ib,beta非常大,则E极电流几乎由ic完全提供,这样只要把可变电阻调整为5.7kohm就可以满足ic=beta * ib这个条件。 所以假设成立,该三极管工作在放大区。
② VCC=3V,问三极管工作在哪个区?
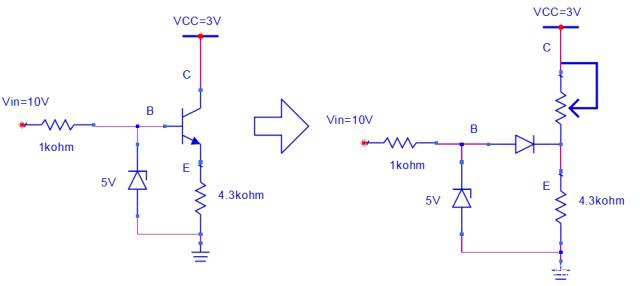
左边是原理图,右边是等效威廉希尔官方网站 图
答:同样由于有5V稳压管存在,B为5V,减去二极管管压降0.7V,得到E为4.3V,所以E极电流为1mA,假设工作在放大区ic=beta * ib,beta非常大,则E极电流几乎由ic完全提供,但是此时VCC=3V,Vce=-1.3V,再怎么减小可变电阻的阻值都不能提供1mA的电流,也就实现不了ic=beta * ib,所以假设失败,工作在饱和区。
4、数字威廉希尔官方网站 与模拟威廉希尔官方网站
模拟威廉希尔官方网站 中使用三极管时,基本上是工作在放大区,因为模拟威廉希尔官方网站 中一个重要的功能就是线性放大。 只有在放大区才有ic=beta * ib这一线性放大关系。
数字威廉希尔官方网站 中使用三极管时,基本上是工作在饱和区和截止区。 因为数字威廉希尔官方网站 只有“0”和“1”两种状态,最重要的一个功能是非门,即从“0”变到“1”,或从“1”变到“0”,其他逻辑关系都是用这个非门威廉希尔官方网站 衍生出来的。
当三极管工作在饱和区时,实现“1”变到“0”:
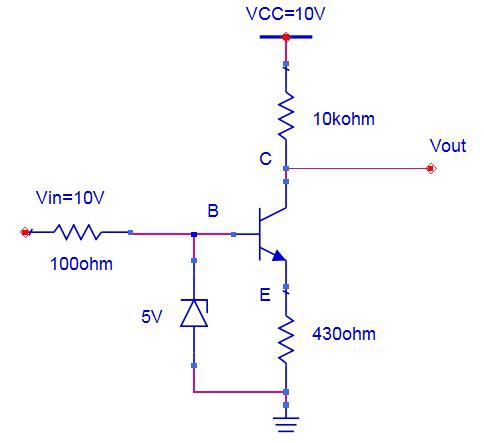
上面原理图表面,当输入Vin为10V高电平时,由于有5V稳压管存在,B为5V,减去二极管管压降0.7V,得到E为4.3V,所以E极电流为10mA,同样先假设工作在放大区ic=beta*ib,由(10V-4.3V)/10kohm=0.57mA可得,就算可变电阻调节为0ohm,也无法从C极提供10mA的电流。 所以假设失败,三极管工作在饱和区。 此时,Vout约为0.43V为低电平。 从而实现从“1”到“0”。
当三极管工作在截止区时,实现“0”变到“1”:
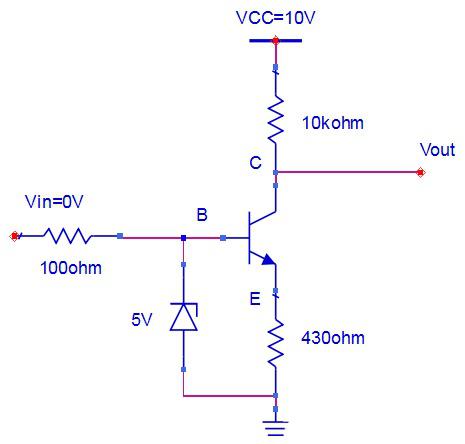
当输入电压为0V时,稳压二极管不能导通,无法起到稳压5V的作用,BE直接的二极管无法导通,可变电阻这时取最大值,近似为无穷大,三级管开路,输出Vout为VCC等于10V,为高电平,从而实现了从“0”到“1”。
总结NPN、PNP的等效威廉希尔官方网站 很重要,要理解可变电阻和三极管工作区域的关系。
模拟威廉希尔官方网站 工作在放大区,数字威廉希尔官方网站 工作在饱和区和截止区。
-
三极管特性曲线2017-11-27 56779
-
三极管三种工作状态特点分析及判断2018-09-28 190006
-
如何快速确定三极管的工作状态三极管的三种工作状态分析判断2019-05-03 71650
-
三极管的工作状态2019-06-18 16945
-
三极管的工作状态判断方法2008-07-14 18312
-
三极管工作特性2015-11-13 1314
-
什么是三极管的倒置状态?三极管倒置状态的应用2021-03-25 9160
-
三极管的三种工作状态 三极管在威廉希尔官方网站 中的作用2021-10-02 30686
-
三极管的三个工作状态2022-09-06 5219
-
三极管的工作状态、电流关系2022-11-21 14221
-
三极管的三种工作状态及动态特性2023-02-21 3343
-
判断三极管工作状态的方法2023-02-22 53473
-
N型三极管的工作状态2023-11-06 1607
-
什么是截止状态?如何才能使三极管进入截止工作状态呢?2023-11-23 5221
-
什么是三极管的饱和工作状态?如何才能让使三极管进入饱和工作状态呢?2023-11-23 8473
全部0条评论

快来发表一下你的评论吧 !

