如何在PLL输出端产生最低的相位噪声？

锁相环 (PLL) 在当今的高科技世界中无处不在。几乎所有商业和军用产品都在其运行中使用它们，相位（或 PM）噪声是一个主要问题。频率（或 FM）噪声密切相关（瞬时频率是相位的时间导数）并且通常在相位噪声的保护伞下考虑（也许两者都可以被认为是“角度噪声”）。幅度（或 AM）噪声是另一个考虑因素。

虽然两者都会影响 PLL 性能，但振幅噪声通常是自限性的，不会产生任何影响。因此，PLL 输出和 RF 组件的相位噪声是主要问题。当然，输出相位噪声是最重要的问题——它主要取决于每个组件的相位噪声。

许多因素都会导致元件相位噪声，例如电源、EMI 和半导体异常等等。了解这些因素使我们能够实施组件相位噪声的缓解策略，并最终实施输出相位噪声。

我们讨论的 PLL 属于模拟硬件类型，而不是数字或软件类型。这种 PLL 的一般拓扑结构是一个单环路系统，其中包含精密参考、参考分频器、反馈分频器、可能的预分频器、电压或电流（也称为电荷泵）鉴相器、环路滤波器和压控振荡器 (VCO) . 这些组件可能都是分立的，或者其中一些可能包含在 IC 中。无论如何，我们展示了如何分析一般的相位噪声，以及 RF 分量相位噪声如何通过 PLL 传播以确定其输出相位噪声。

在第 1 部分中，我们讨论了相位噪声的一些简要理论和典型测量及其分析（建模、仿真和传播），并详细展示了大多数计算机辅助设计 (CAD) 应用程序使用的方法。

相位噪声的简要理论和典型测量

相位噪声是一个重要而复杂的课题，研究正在进行中，对其起源的理解也很脆弱，数学基础也有问题。然而，许多近似值和变通方法被用来产生极好的理论和实践结果。1,2,3这是一个成熟的学科，有很多可用的文献。有几种仪器可以精确测量相位噪声，并且无数带有 PLL 的现场系统都具有受控的相位噪声特性。

在这里，我们简要回顾时域和频域中的相位噪声理论，以及基带 (BB) 领域（对 RF 载波信号进行相位调制的 BB 噪声信号）和 RF 领域（RF由 BB 噪声信号进行相位调制的载波信号）。

此外，我们还总结了频域中两个领域的典型相位噪声测量，当然，它们是同一现象的不同等效表示，并给出相同的结果。

BB 领域被认为是不太重要的领域，但对于相位噪声的起源很重要，并且提供比 RF 领域更好的测量精度。RF 领域被认为是更重要的领域，并且对相位噪声的可观察表现很感兴趣，尽管它的测量精度不如 BB 领域。1,8此外，我们调查了两种测量类型的等效性。

正如所有物理学中众所周知的那样，存在确定性和非确定性（也称为随机、随机或概率）过程。在 PLL 中，这些过程是信号，可以在时域和频域两个域中表示，两个域通过傅立叶变换通过变换理论相关联。

要使用（在本例中为连续）变换理论，系统被建模为（连续）线性时不变网络，这意味着 PLL 必须处于锁定状态。相反，处于解锁状态的 PLL 模型是非线性的；因此，不能应用变换理论。

此外，域之间的转换对于确定性信号是直接的，对于随机信号是间接的。直接意味着直接在时域和频域之间进行变换，因为存在直接变换。间接是指域之间的转换有一个中间步骤，就是计算随机信号的自相关函数，取其时间平均，然后进行变换，因为直接变换是不存在的。6个

然后，在 RF 系统或 RF 组件中，当已知和未知来源的内部和/或外部 BB 随机（噪声）信号对系统或组件的内部 RF 确定性（载波）进行相位调制时，会产生相位噪声） 信号。当然，相位噪声是一种随机现象或信号，因此充满了间接变换。

通常，对于频域中的随机信号，作为电压谱密度 (VSD) 的频谱是不存在的。然而，频谱确实以功率谱密度 (PSD) 的形式存在，只有幅度信息而没有相位信息。相比之下，对于频域中的确定性信号，频谱通常确实以 VSD 形式存在，具有幅度和相位信息，当然，扩展后也具有 PSD。

此外，在 BB 领域的频域中，频谱是低通（或准低通）函数，而对于 RF 领域，频谱是带通函数。此外，在本次讨论中，我们仅使用正单边 (OS) 频谱和正单边带 (SSB) 相位噪声信息，而不是双边 (TS) 频谱和双边带 (DSB) 相位-噪音信息。

我们还注意到，在时域中，相位噪声通常称为相位抖动，而在频域中，它通常称为规定相位噪声。这两个域中的现象通过瞬时频率定义为相位的时间导数而相关联。1,8,10

考虑到上述背景，我们简要回顾了时域和频域的一些理论以及BB 领域的 域之间的转换。在这个领域，我们的理论和分析原则上基本上存在，因为我们的随机（噪声）信号在时域（这是我们的分析开始的地方）没有解析表达式。因此，经过变换后，频域上没有解析表达式。我们有以下数学表示和变换步骤：6,7,8

1.时域函数或相位波形，它是一个真实的（非复杂的）随机过程，具有零均值高斯概率密度函数，ϕ(t)：

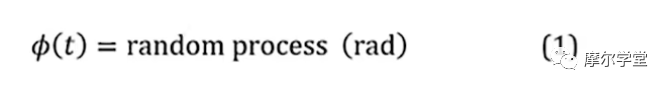
其中t是时间。

2. (1)的自相关函数，R ϕ (t, τ)：

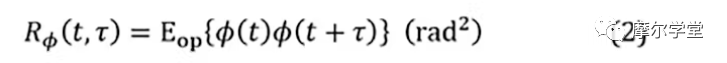
其中τ是测量之间的正时间增量，E op {...}是统计平均运算符。

3. 等式 2 的时间平均值的傅立叶变换，给出非归一化 (UN) BB频域函数或 PSD，W ϕ ( ξ)或WdB ϕ( ξ)：

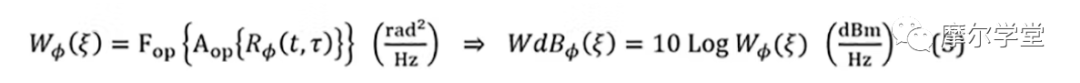
其中ξ是频率，A op {...}是时间平均算子，F op {...}是傅里叶变换算子。典型的相位波形图及其 UN BB PSD如图 1a 和 1b所示。

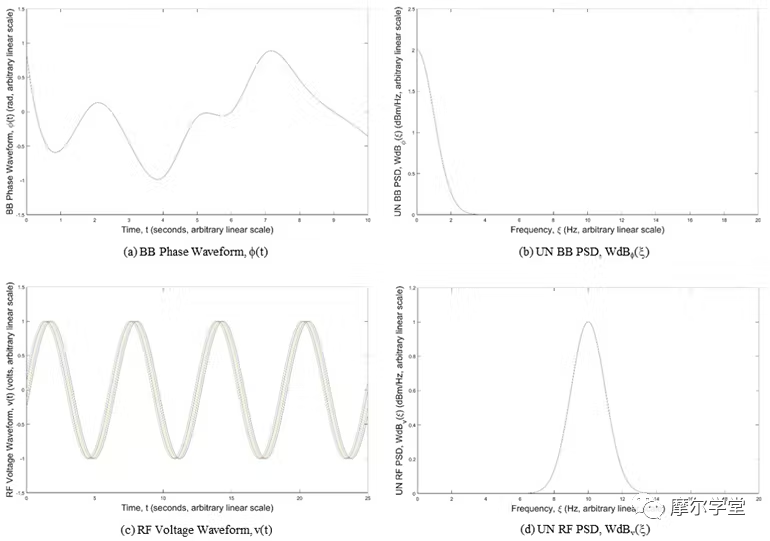
1. (a) 基带 (BB) 相位波形 ϕ(t)，(b) 非归一化 (UN) BB 功率谱密度 (PSD)，Wdb ϕ (ξ)，(c) 的相位噪声理论中的典型图) RF 电压波形 v(t)，以及 (d) UN RF PSD，Wdb v (ξ)。

接下来，我们简要回顾时域和频域中的类似理论以及射频领域的域间转换。在这个领域，我们的理论和分析是相当分析的，因为在时域中我们的确定性（载波）信号有一个相当分析的表达式（这又是我们分析的起点）。因此，经过变换后，在频域上有一个相当解析的表达式。

对于≤ 0.2 弧度（≤ 11.5°）的“合理”相位波形偏差（也称为小角度...、小调制指数...或窄带 PM...近似值），其中 PM 频谱与DSB AM 频谱——这是所有实际相位噪声问题的情况——我们有以下数学表示和变换步骤（为简洁起见未显示细节）：7、8、10

4.时域函数或电压波形（也是BB参数的函数），v(t)：

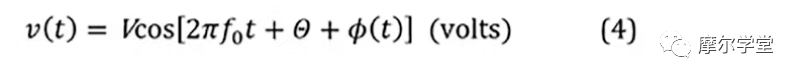
其中V是统计平均振幅，f 0是载波频率，Θ是初始相位（V是一般振幅的特例，V + a(t)，其中a(t)是统计零均值a(t) = 0的振幅噪声，因为如前所述，它是自我限制的并且没有任何后果）：

5. 等式 4 的自相关函数（同样也是 BB 参数的高斯概率密度函数），R v ( τ )：

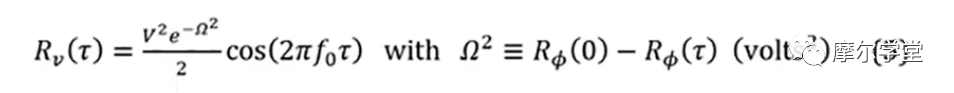
其中R φ (0)是R φ ( τ) ，其中τ = 0，这是φ(t)的方差。

6. 等式 4 的时间平均值的傅立叶变换（同样也是 BB 参数的函数）给出 UN RF频域函数或 PSD，W v ( ξ)或WdB v ( ξ)：

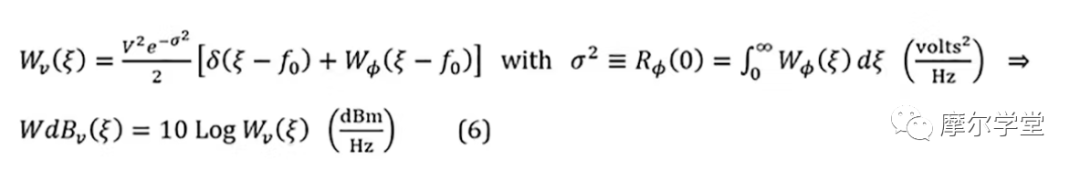
其中d ( ξ– f 0 )是 Dirac delta 或单位脉冲函数，W ϕ ( ξ– f 0 )是 UN BB PSD，W ϕ ( ξ)，通过调制过程从 BB 领域转换到 RF 领域。典型的电压波形图及其 UN RF PSD如图 1c 和 1d所示。

需要注意的是，如果ϕ(t)是严格平稳的（一个合理的假设），则可以证明v(t)至少是广义平稳的。在这种情况下，Weiner-Khinchin 定理成立，R ϕ (t, τ )和R v (t, τ )仅成为 τ 的函数，[ R ϕ (t, τ ) → R ϕ ( τ )和R v (t, τ ) → R v ( τ )]，因此不需要找到R ϕ ( τ )和R v ( τ )的时间平均值。因此，W ϕ ( ξ)和W v ( ξ)是R ϕ ( τ )和R v ( τ )本身的傅里叶变换。1,6,7,9

然后，根据上述简要理论，我们总结了频域中 BB 和 RF 领域相位噪声的典型测量。

BB 领域的测量

在上面的 UN BB PSD 中，选择了一个特定的频率，并将其在 1 Hz 带宽中的功率除以低通频谱上的总积分功率，得到归一化 (NM) BB PSD，L ϕ ( ξ )或LdB ϕ ( ξ)：

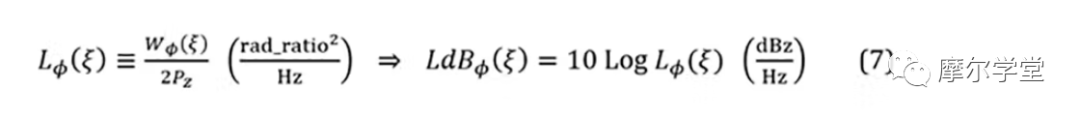
其中ξ是特定频率，P z是总积分低通功率，dBz 是相对于P z的分贝数。测量是间接的，使用信号源分析仪，解调、测量、处理和显示 BB 信号以产生L ϕ ( ξ)或LdB ϕ ( ξ) [ W ϕ ( ξ)包含 DSB 信息，因此因子L ϕ ( ξ)的计算需要 2给 SSB 信息]。它被认为比在 RF 领域所做的更准确。1,8

射频领域的测量

在上面的 UN RF PSD 中，选择了一个特定的载波偏移频率。它在 1 Hz 带宽内的功率除以带通频谱上的总积分功率，得到 NM RF PSD、L v (f)或LdB v (f)：

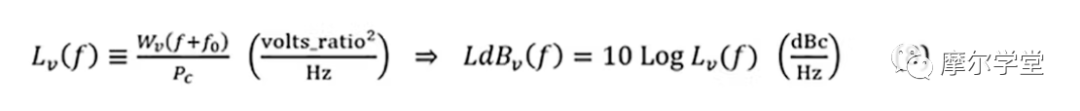
其中f是载波的特定偏移频率 ( f = ξ − f 0其中ξ≥ f 0 ), P c是总积分带通功率，dBc 是相对于P c的分贝数。测量是直接的，使用具有相位噪声处理能力的频谱分析仪测量、处理和显示射频信号以产生L v (f)或LdB v (f)。它被认为不如在 BB 领域中所做的那样准确。1,8

两种测量的等效性

如前所述，L ϕ ( ξ)或LdB ϕ ( ξ)和L v (f)或LdB v (f)是同一现象的不同表示，逻辑上应该对所有实际相位噪声问题给出相同的结果（其中，也如前所述，相位偏差被认为是“合理的”）。因此，对于这种情况，它们是等价的并且给出相同的结果，称为 NM PSD、L(f)或LdB(f)。BB 和 RF 领域下标 ( ϕ和v) 被删除并且不使用下标（即使是“合理”条件也有一些异常，必须使用具有学术和实践论据的近似值）：1,10

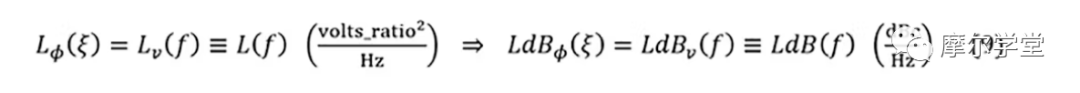
其中，典型显示的f是 x 轴载波的偏移频率，单位为 Hz，对数标度，LdB(f)是 y 轴的 NM RF PSD，单位为 dBc/Hz，线性标度规模，对于上述间接和直接测量，最终将一切与 RF 领域相关联（图 2）。

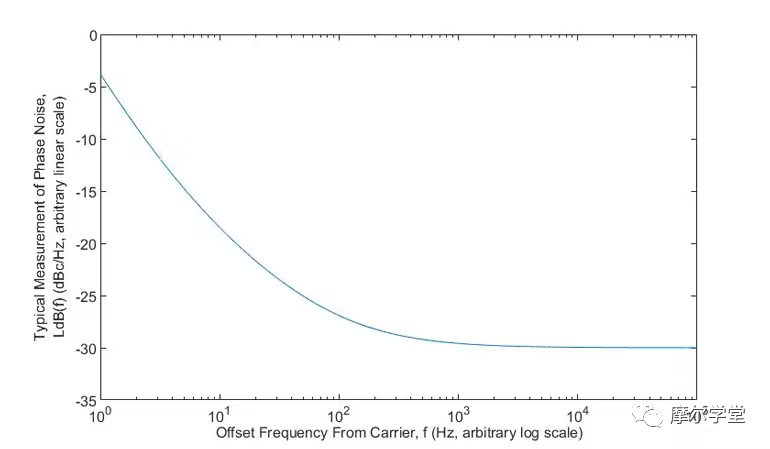
2. 频域中基带和射频领域相位噪声的典型测量。

需要注意的是，如果不满足“合理”条件，则必须使用贝塞尔函数数学将L ϕ ( ξ)与L v (f)联系起来。因此，这两种测量不会等同，会给出不同的结果，并且会被认为是灾难性的问题。

相位噪声的分析（建模、仿真和传播）

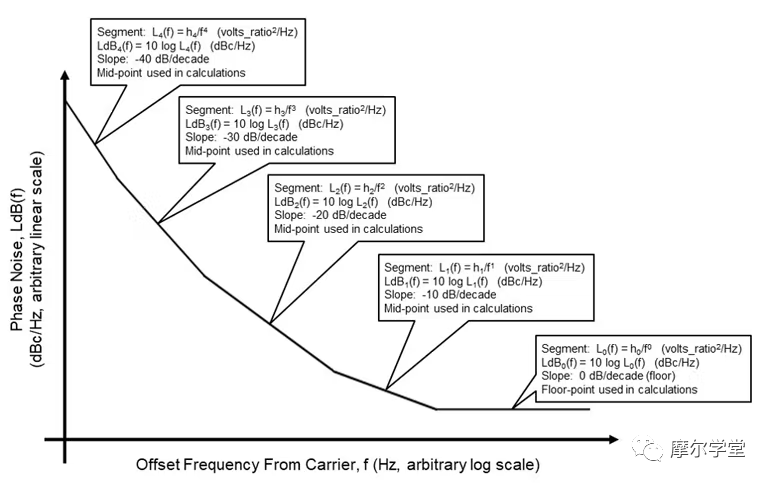
3. 用于相位噪声分析（建模、仿真和传播）的一般相位噪声模型。

有了以上信息，我们现在开始分析 PLL 中的相位噪声，以及一般如何对其进行建模和仿真。还讨论了 RF 分量相位噪声如何通过 PLL 传播以确定其输出相位噪声。通常，相位噪声可以使用“通用相位噪声模型” （图 3）及其标准整数幂级数进行有效建模：

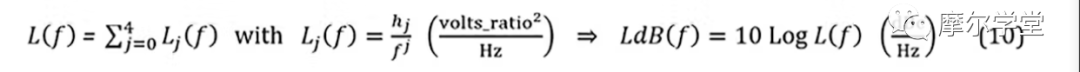
其中h是加权系数，f是载波的偏移频率。1,7然后使用任何标准应用程序对其进行仿真（在本例中，我们使用 MATLAB）。最后，组件相位噪声通过 PLL 的传播以确定其输出相位噪声是使用通用 PLL 模块“图表和相位噪声传播模型”完成的（图 4）。

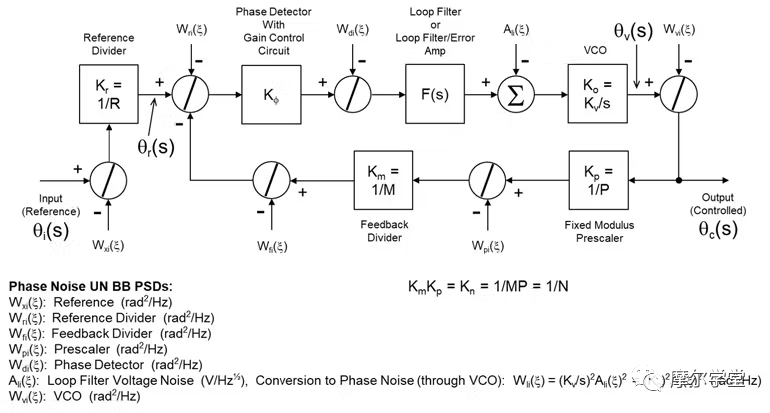
4. 用于相位噪声分析（建模、仿真和传播）的通用 PLL 框图和相位噪声传播模型。

此外，为了简化分析，所有组件的相位噪声都近似为不相关（合理的假设），以便它们的 NM PSD 直接相加，而不必处理相关信号，这会使分析变得非常复杂。然后使用以下相位噪声分析程序进行分析：4,5

1. PLL 必须表示为（在本例中为连续的）线性时不变网络，这意味着它必须锁定在其输出之一。

2. 所有组件的相位噪声必须近似为不相关。

3. 每个组件的相位噪声图都是从其数据表中获得的，“通用相位噪声模型” （图 3）适合每个组件的图，以确定匹配的通用模型的部分（其中一些可能不存在）每个组件的情节。

4. 对于每个组件的拟合通用相位噪声模型，一个相位噪声点，LdB j (f k ) ( j,k = 0,a; 1 ,b ; 2,c ; 3,d ; 4,e )，在每个获得段用于计算（通常使用段内的中点）。将所有对数值转换为线性值，LdB j (f k ) Þ L j (f k )：

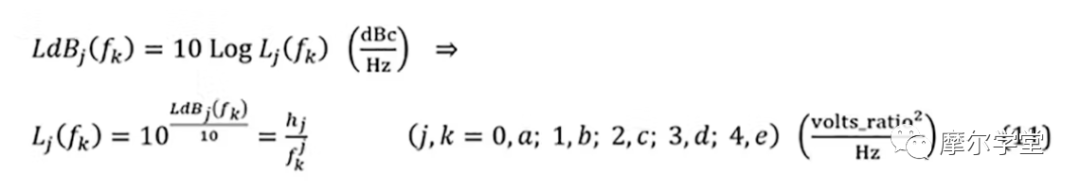
5. 每个组件的拟合通用相位噪声模型系数h j是使用来自步骤 4 的相位噪声点（其中一些可能为零）计算的：

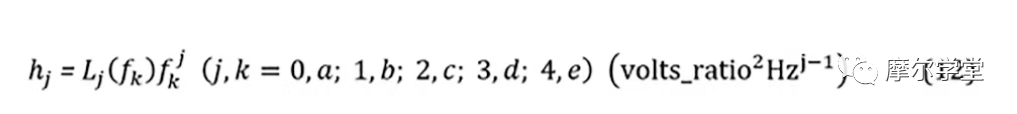
6. 来自步骤 5 的每个组件的拟合通用相位噪声模型系数h j用于形成每个组件的相位噪声模型L ci (f)：

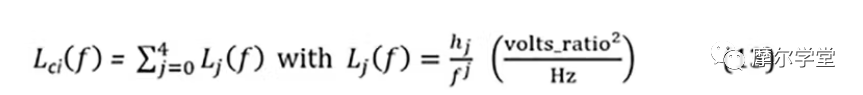
可以对其进行模拟以产生分量相位噪声曲线。

7. 来自步骤 6 的每个组件的相位噪声模型L ci (f)乘以其适用的传递函数（输出或误差；稍后讨论）幅度平方，| T(f) | 2，得到其传播的相位噪声模型，L co (f)：

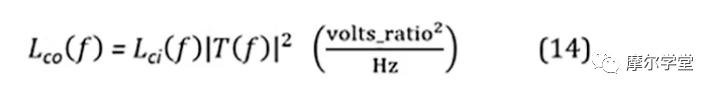
可以对其进行模拟以产生组件传播的相位噪声曲线。

8. 来自步骤 7 的每个组件的传播相位噪声模型L co (f)与所有其他相加在一起以获得输出相位噪声模型L至(f)：

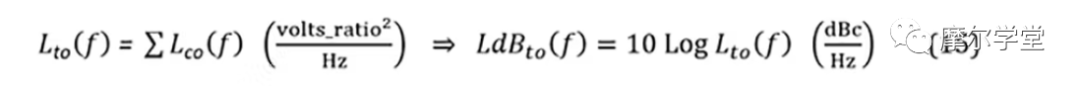
可以对其进行仿真以产生输出相位噪声曲线。

这就是我们的相位噪声分析（建模、仿真和传播）过程。如前所述，这是大多数 CAD 应用程序用于相位噪声分析的方法。

审核编辑：刘清