定义和测试高速ADC中的动态参数

本系列文章的第一部分讨论了通信、仪器仪表和数据采集应用中使用的高速数据转换器（在本例中为模数转换器或短ADC）中最为关键的常见定义。本文旨在帮助读者更好地了解常见参数，如信噪比（SNR）、信噪比和失真（SINAD）、总谐波失真（THD）和无杂散动态范围（SFDR）。在本系列文章的第二部分中（有关进一步阅读，请参见“高速ADC的动态测试”），这些参数定义通过在实际测试场景中测量来进行测试。

ADC的动态规格在数字通信、超声成像、仪器仪表和IF数字化等高速应用中非常重要。以下讨论提供了每个参数的定义和数学基础，提供了评估高速ADC动态性能的有用技术，并解释了动态参数如何与ADC性能相关。这个由两部分组成的讨论的第 1 部分涵盖了这些规范的定义：

信噪比 （SNR）

信噪比和失真比 （SINAD）

有效位数 （ENOB）

总谐波失真 （THD）

无杂散动态范围 （SFDR）

双音互调失真 （TTIMD）

多音互调失真 （MTIMD）

电压驻波比 （驻波比）

在解释如何测量这些参数时，第 2 部分提供了对动态性能测试的实际方面的见解。请注意，某些规范允许使用多种方法进行测量甚至定义。因此，第 2 部分的测试技术代表一种方法，不是强制性的。所描述的任何方法都可以根据需要扩展或更改，以适应手头的应用。

在测试高速模数转换器时，可以仿真用于量化模拟威廉希尔官方网站 线性度的频谱分析仪的操作。对于该仪器和测试程序，动态规格通常使用快速傅立叶变换（FFT）在频域中表示。在这两种情况下，数据输出都表示该FFT的大小。例如（图1），考虑一个80Msps、10位ADC的FFT图，该ADC专为超声成像和基带/中频的数字化而设计和优化。这种FFT图包含大量信息，并且可以快速生成。但是，要使用FFT，必须了解其参数是如何定义的。

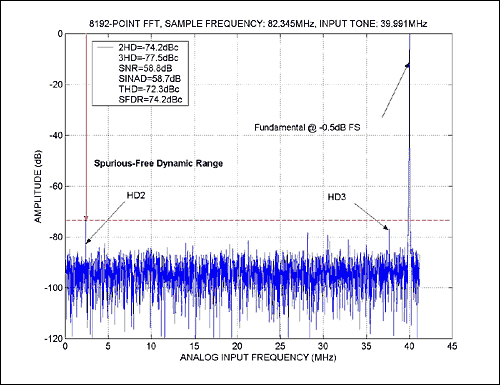
图1.MAX8192的1448点FFT曲线

信噪比 （SNR）

对于由数字样本完美重建的波形，SNR 是均方根（均方根）满量程模拟输入与其均方根量化误差 （A量化[有效值] = A低音水平/√12 = A裁判/[2N ×√12]）。正弦波的均方根值是其峰峰值的一半除以√2，量化误差是模拟波形与其数字重建副本之间的差异，其特征是阶梯形传递曲线。差分函数类似于锯齿波，每个样本在 +1/2LSB 和 -1/2LSB 水平之间振荡一次（LSB 是最不重要的位）。差分函数的均方根值是其峰值（1/2LSB）除以√3。对于理想的N位转换器，SNR定义为

信噪比 - 2N× √3 / √2 = 1.23 × 2N.

大多数动态规格表示为相对测量值的比率，而不是绝对单位。因此，理想ADC的信噪比由交流功率等于AREF / （2 × √2）的满量程正弦输入驱动，单位为分贝，为

SNRdB = 20 × log10 (AIN[rms] / AQUALITIZATION[rms]
SNRdB = 20 × log10 (AREF / [2 × √2] / AREF / [2N × √12])
SNRdB = 6.02 × N + 1.76

除量化噪声外，SNR还会因许多噪声源而降低（见附录1）。数据转换器的分辨率和量化电平都有助于确定其本底噪声。因此，正弦输入信号的实际SNR可以描述为：

SNRdB = 20 × log10 (ASIGNAL[rms] / ATOTAL_NOISE[rms],

其中 A信号[rms] 表示模拟输入信号的均方根幅度，ATOTAL_NOISE[rms] 是限制转换器动态性能的所有噪声源（热噪声、量化噪声等）的均方根总和。将此定义应用于MAX10等1448位ADC，在58MHz奈奎斯特频率（f样本= 80毫秒）。该SNR占理想94位ADC所表现出的~62dB SNR的10%。

对于由正弦输入驱动且幅度等于ADC满量程输入的ADC，最大理论SNR为：

SNRdB = 6.02 × N + 1.76 + 10 × log10 (fSAMPLE[rms] / 2 × fMAX,

其中 f.MAX描述输入音的最大带宽，以及 f样本是转换器的采样频率。根据这个等式，请注意，SNR随着采样频率的增加而增加，超过奈奎斯特速率（2 × f.MAX).这种效应称为处理增益，是由量化噪声功率（固定且与带宽无关）随着采样频率的增加而扩展引起的。这种“过采样”有助于最大限度地减少噪声的影响，噪声落入直流至f的奈奎斯特带宽.MAX.

信噪比和失真比 （SINAD）

对于正弦输入信号，SINAD 定义为均方根信号与均方根噪声的比值（包括 THD 的前 N 次谐波：通常是 2 次至次 5 次谐波）。对于给定的采样率和输入频率，SINAD提供模拟输入信号与噪声加失真的之比（以dB为单位）。SINAD描述了ADC动态范围的质量，表示为最大幅度输出信号与转换器可以产生的最小输出信号增量之比。在数学上，SINAD 被描述为

SINADdB = 20 × log10 (ASIGNAL[rms] / ANOISE+HD[rms]),

其中 A信号[均方根]表示均方根输出信号电平和A噪音+高清[rms] 描述奈奎斯特频率以下所有频谱分量的均方根和，不包括直流电。SINAD 的质量还取决于正弦输入音的幅度和频率。

有效位数 （ENOB）

对于实际（相对于理想）ADC，通常用来代替SNR或SINAD的规格是ENOB，它是特定输入频率和采样速率下ADC精度的全局指示。它根据转换器的数字数据记录计算为 N - log2测量值与理想均方根误差之比：

ENOB = N ×日志2（一MEASURED_ERROR[有效值] / AIDEAL_ERROR[有效值]），

其中 N 是数字化位数，AMEASURED_ERROR[rms] 是平均噪声，AIDEAL_ERROR[rms] 是量化噪声误差，表示为 q / √12 = A司 司长/ [2N× √12]。一个司 司长是转换器的满量程输入范围，由基准电压A决定裁判.

ENOB = log2 (AFS / AMEASURED_ERROR[rms] × √12)_ERROR[有效值] × √12）

或

ENOB = log2 (AREF / AMEASURED_ERROR[rms] × √12)

ENOB通常取决于所施加的正弦输入音的幅度和频率，并且必须为此特定测试指定两者。该方法将被测ADC产生的均方根噪声与具有相同分辨率的理想ADC的均方根量化噪声（以位为单位）进行比较。如果具有给定频率和幅度的正弦波输入的实际10位ADC的ENOB = 9.0位，则对该输入产生的均方根噪声电平与理想的9位ADC相同。

与SINAD直接相关，ENOB经常表示为：

ENOB = （SINAD - 1.76） / 6.02。

理想ADC的误差仅由噪声组成。然而，对于实际转换器，测量误差包括量化噪声以及像差，如输出代码缺失、AC/DC非线性和孔径不确定性（抖动）。基准电压源和电源线路上的噪声也会降低ENOB的性能。

总谐波失真 （THD）

每当ADC对周期性信号进行采样时，动态误差和积分非线性都会产生谐波失真。对于纯正弦波输入，输出谐波失真分量位于频谱值处，其非混叠频率是所施加的正弦输入音的整数倍。非混叠频率的幅度取决于施加的输入正弦波的幅度和频率，通常以相对于施加的正弦波输入幅度的dB比给出。它们的频率通常表示为所施加的正弦输入信号频率的倍数。

THD 是输出信号的快速傅里叶变换 （FFT） 频谱中所有谐波的均方根和。根据定义，所有谐波都包括在内，但前三个（在大多数情况下）代表了给定转换器中输出失真的主要贡献。在通信和RF/IF应用中，THD对于ADC来说通常比描述转换器静态性能的直流非线性规格更重要。THD由下式给出

THDdBc = 20 × log10 (√{AHD_2[rms]² + AHD_3[rms]² + ... + AHD_N[rms]²} / A[fIN]rms),

其中 A[f在]有效值是均方根基波幅度，AHD_2[有效值]通过 AHD_N[有效值]表示二阶至N次谐波的均方根幅度。选择集合中包含的谐波分量通常是在希望包括具有很大一部分谐波失真能量的所有谐波和排除离散傅里叶变换（DFT）频率箱（其能量成分主要由随机噪声主导）之间进行权衡（见附录2）。

除非另有说明（请参阅数据手册中的制造商规格），否则THD通常由正弦模拟输入音的最低2至10次谐波（包括<>至<>次谐波）组成。请注意，制造商可以参考载波频率或基波 （dBc） 以分贝 （dB） 或分贝为单位指定其 THD 值。这两个单元都是常用的，THD是根据模拟输入音定义的。

无杂散动态范围 （SFDR）

术语无杂散动态范围通常用于谐波失真和杂散信号被视为采样纯正弦输入音输出频谱中不希望的杂散的情况。SFDR表示ADC的可用动态范围，超过该范围，频谱分析会带来特殊的检测和阈值问题。虽然与THD类似，但SFDR解决了转换器的带内谐波特性。

无杂散动态范围是指定频率范围内基波（最大信号分量）的均方根幅度与最大失真分量的均方根值之比。在设计良好的系统中，这种杂散应该是基波的谐波。SFDR很重要，因为噪声和谐波限制了数据转换器的动态范围。例如，在IF带通转换器中，杂散可以解释为相邻信道信息。

在其他应用中，低电平雷达信号等目标信号无法与谐波成分区分开来。为了帮助确定SFDR值，建议使用带有集成数模转换器（DAC）的频谱分析仪进行重建。通常的步骤是施加接近满量程的输入信号（首选输入音幅度为-0.5dB至-1dB FS），测量响应，然后采集并测量最大杂散分量的幅度。SFDR是第一次测量与第二次测量的比率。SFDR也可以通过检查被测ADC的FFT频谱（图）来确定。

对于频谱纯正弦波输入，SFDR是基频处平均DFT值的幅度之比（A[f在]） 到最大振幅谐波的平均 DFT 值的幅度 （AHD_MAX[有效值]）或杂散信号分量（ASPUR_MAX[有效值]）在整个奈奎斯特带上观察到。

SFDRdBc = 20 × log10 (|A[fIN]rms| / |AHD_MAX[rms]|)

or

SFDRdBc = 20 × log10 (|A[fIN]rms| / |ASPUR_MAX[rms]|)

通常，SFDR 是幅度和频率 （A[f ） 的函数在]， f在），在某些情况下，甚至采样频率（f样本） 的受测转换器。因此，在测试ADC的无杂散动态范围时，应指定采样频率以及输入频率和幅度。

双音互调失真（双音IMD）

IMD通常是由调制引起的，当ADC对由两个（或多个）正弦波信号组成的信号进行采样时，就会发生IMD。IMD光谱分量可以在两个总和（fIMF_SUM） 和差值 （fIMF_DIFF） 基频（输入频率音）或信号组频率的所有可能的整数倍的频率。

对于双音IMD测试，输入测试频率f合1和 f合2（f合2> f合1） 设置为DFT箱的奇数且远离奈奎斯特频率（f样本/2).这些设置保证两个输入音之间的差异始终是偶数个DFT箱。得到的频谱（图2）是平均幅度频谱A[f基金组织]有效值.双音输入信号的IMD幅度位于指定的和频和差频：

fIMF_SUM = |m × fIN1 + n × fIN2| and |m × fIN1 - n × fIN2|,

其中 m 和 n 是正整数。m 和 n 大于零的条件创建二阶(2fIN1 + fIN2, 2fIN1 - fIN2, fIN1 + 2fIN2, and fIN1 - 2fIN2, 3fIN1 and 3fIN2) 互调产物。

由于测试参数通常是特定于应用的，因此不需要（或提供）特定的指南来指定用于互调测试的频率和信号幅度。|f 的大小合2， G合1|完全取决于应用程序和所需的信息。请注意，两个输入音的微小差异会导致互调频率聚集在f的谐波失真分量周围合1和 f合2.

双音互调失真通常是幅度（A[f）的函数合1]有效值和 A[f合2]有效值） 和频率 （f合1和 f合2） 的输入组件。因此，您必须指定执行双音IMD测量的输入音调和振幅。输入测试信号必须几乎没有互调和谐波失真。对于动态范围更大、带宽更宽的ADC，这一条件越来越难以实现。

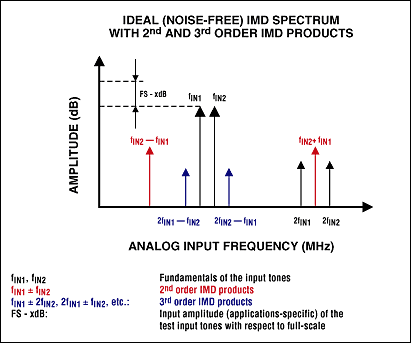
图2.该图显示了具有二阶和三阶IMD乘积的双音IMD频谱。

两个信号发生器包含输出电平威廉希尔官方网站 ，并通过平衡或隔离输出或任何其他耦合威廉希尔官方网站 连接，可以轻松产生IMD效果。因此，为避免测试信号中的互调失真，应在其线性范围内很好地操作功率分配器/合路器（用于组合或分离两个输入音）。图3显示了2位、3Msps ADC的双音IMD和二阶和三阶IMD产品。为获得最佳结果，该ADC的双音包络选择为-10.80dB FS，并将两个输入音的幅度归一化为-0.5dB FS。

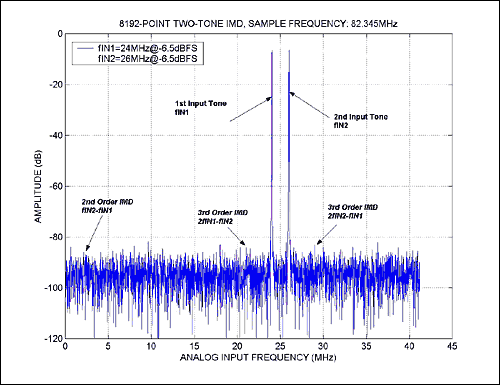
图3.MAX1448的双音交调失真，具有样本= 82.345兆赫。

多音调互调失真（多音IMD）

系统设计中经常使用多音互调失真测试来确定信号动态范围的限制、不同信号组的有用频段，以及在哪里设置输入信号的本底噪声以掩盖给定ADC的小互调分量。单音谐波失真的测量有助于获得有关给定ADC线性度的一般概念，但此类数据不会直接导致预测独立输入信号音调互调性能的有用测量值的模型。

典型的测试程序具有计算机控制的DAC，该DAC在DFT二进制中心频率上产生由一组正弦波组成的信号。随着音调幅度均匀增加，从本底噪声开始，一直到削波开始的满量程ADC电平，音调之间的间隙可作为观察点来分析任何产生的IMD。此类测试提供的结果类似于噪声功率比（NPR）测试（见附录3）。但是，它们可以更好地模拟预期的信号组波形。

电压驻波比 （VSWR）

在高速数据转换器的数据手册中很少指定，VSWR是实际阻抗与所需或预期阻抗之间的不匹配之比。它可以通过施加测试信号并测量ADC输入端子的反射系数来计算。计算如下，VSWR与简单端接阻抗Z的反射系数ρ直接相关T:

VSWR = （1 + |ρ|） / （1 - |ρ|），
其中 ρ = （ZT- Z0） / （ZT( 90)

ZT表示ADC输入端接阻抗和Z0表示传输线阻抗（标称值为50Ω）。为了补偿测量中的威廉希尔官方网站 误差，建议使用校准标准（通常为短路、开路和50Ω）。

结论

前面的讨论是对高速数据转换器最重要的动态规格的回顾。本文将在第 2 部分中结束，其中详细介绍了最适合捕获数据记录以及使用这些记录来测试上面定义的动态性能参数的工具。除了 测试 设置 信息 外， 第 2 部分 还 提供 了 MATLAB® 和 LabWindows/ CVI® 源代码 的 样本， 使 设计 人员 能够 通过 快速 捕获 数据 记录 并 高效 处理 数据 记录 来 分析 ADC 的 动态 性能。

审核编辑：郭婷