通过衰减器和统计模型实现失配损耗和失配不确定性

了解失配损耗对有损线路的影响、通过固定衰减器减少失配损耗的方法以及该误差的统计模型。

失配损耗 （ML）描述了RF信号路径中的多个阻抗不连续性如何导致功率损耗并阻止我们在威廉希尔官方网站 中的两点之间进行有效的功率传输。

在本文中，我们将首先讨论失配损失对有损线的影响。然后，我们将看一个通过固定来减少失配损耗的简单方法 衰减 最后触及这个误差的统计模型。

处理无损线路时的失配损耗

在本系列的上一篇文章中，我们了解了 失配损耗对级联放大器增益的影响 （图1）。

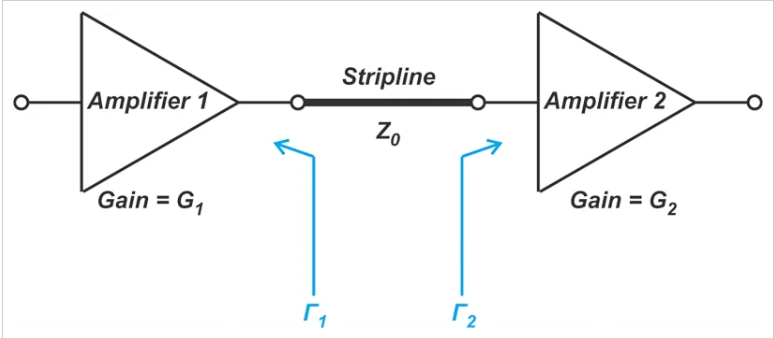
图1. 示例图显示了通过带状线连接的两个放大器。

在这种情况下，放大器1的输出阻抗和放大器2的输入阻抗与线路的 特性阻抗.由于 波反射，部分射频能量无法输送到放大器 2 的输入端。功率损耗由公式1给出：

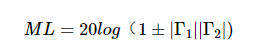
等式 1.

上述等式对应于以下情况： 传输线无损 （增益为 1 或 0 dB）。然而，在实践中，该线路表现出一些衰减。

考虑线路衰减

假设线路电压衰减的大小为 Ac，其中 Ac 以线性项而不是分贝表示，并且值小于单位。图2显示了电压波如何沿正向传播（a1） 受线路衰减的影响。

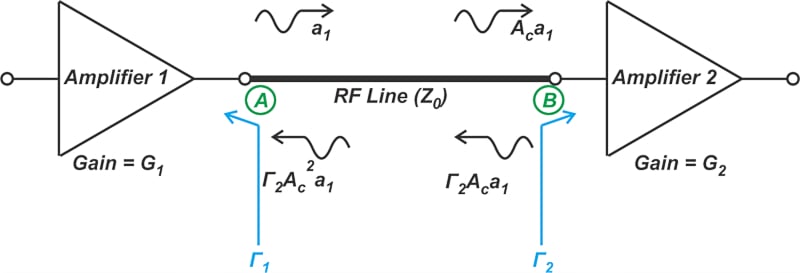
图2. 该图显示了向前传播的电压波如何受到线路衰减的影响。

当信号从A点传输到B点时，它会衰减A倍c.然后信号在B点碰到阻抗不连续性，反射信号经历额外的衰减Γ2.此时，整体衰减因子为Γ2一个c.最后，信号沿线路向A点传播，并额外衰减A。c.通过比较A点的入射信号和反射信号，从A点到线的有效反射系数的大小计算如下：

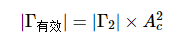
等式 2.

将此结果代入公式1，我们得到衰减为A的电缆的失配损耗c:

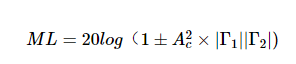
等式 3.

示例 1：查找最小和最大失配损耗

假设在匹配的环境中， 传输线 标称衰减为 2 dB。如果 |Γ1|≤ 0.5 和 |Γ2|≤0.33，失配引起的损失的最大值和最小值是多少？ 

我们首先需要用线性术语找到衰减因子：

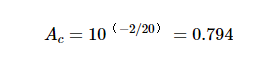
替换 Ac = 0.794, Γ1 = 0.5 和 Γ2 = 0.33 进入公式 3，ML 的最大值和最小值计算为 ML.max = 0.859 dB 和 ML最小 = -0.954 分贝。0.954 dB的负损耗实际上表示功率增益。现在，我们可以使用这些值来查找线路的等效损失。我们知道线路的标称损耗为2 dB。由于反射，可能会增加0.859 dB的损耗或0.954 dB的增益。因此，线路的最大损耗为 2.859 dB，最小损耗为 1.046 dB。

此外，我们还可以说线路的最大增益为-1.046 dB，线路的最小增益为-2.859 dB。如果放大器 1 和 2 的传感器增益为 G1 和 G2，则级联的总增益可以在G之间变化1 + 克2 - 2.859分贝和G1 + 克2 - 1.049分贝

通过衰减器降低失配不确定性

上述讨论为我们提供了一个减少失配不确定性（MU）的通用解决方案。比较等式1和3，我们观察到线的衰减因子有效地降低了反射系数。同样，我们可以故意添加一个匹配的固定衰减器来抑制反射波。如图 3 所示。

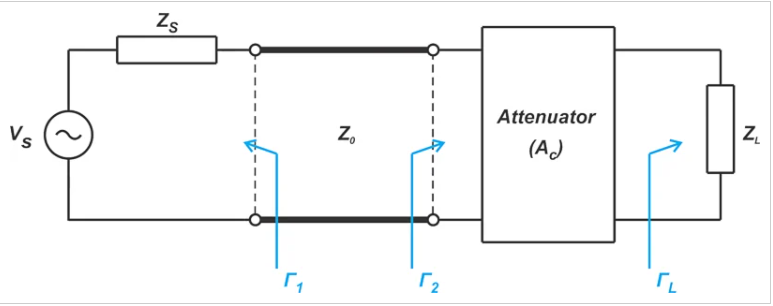
图3. 显示添加匹配的固定衰减器如何抑制反射波的图表。

衰减器输入端的反射系数大小为：

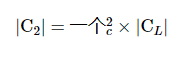
在这种情况下，MU 是：

 

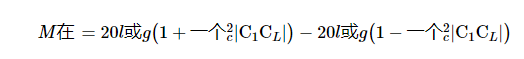
如果需要，我们还可以在线路的输入端口添加一个固定衰减器，如下图4所示。

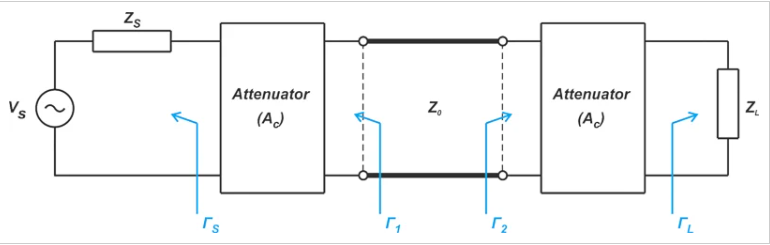
图4. 固定衰减器的示意图被添加到线路的端口。

线输入处的反射系数为：

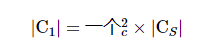
因此，在两个衰减器都到位的情况下，MU 为：

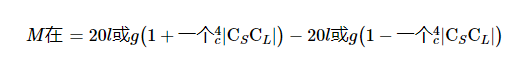
等式 4.

示例2：使用衰减器探索失配不确定性

射频线输入端和输出端的反射系数分别为0.3和0.4，如下图所示。

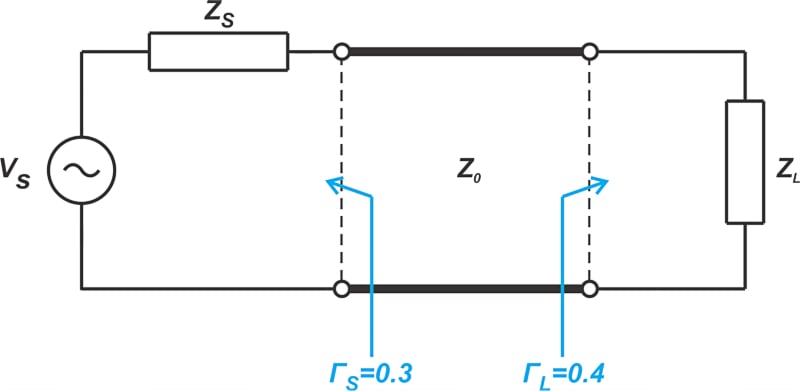
图5. 显示RF线路输入和输出的示例图，ΓS 和ΓL.

此配置中的失配不确定性是什么？如果我们在线路的输入和输出端插入两个3 dB衰减器，新的失配不确定性会是什么？

如果没有衰减器，我们有：

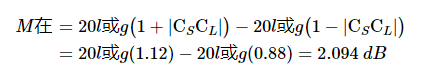
对于 3 dB 衰减器，衰减器的输入输出电压比为：

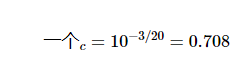
使用公式4，我们找到了双衰减器配置的失配不确定性：

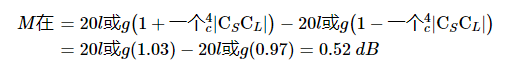
如您所见，衰减器显著降低了失配不确定性。

遮蔽垫 — 应用和其他注意事项

用于减轻阻抗失配的衰减器有时称为“焊盘”、“屏蔽焊盘”或“匹配焊盘”。但是，请记住，术语“匹配焊盘”也用于在 75 Ω 到 50 Ω 之间转换的阻抗转换焊盘，这些是不同的设备。

屏蔽垫通常用于RF信号路径，以使测量更加可靠和可预测。插入遮蔽垫的最佳位置是 阻抗匹配 是最差或最可变的。掩蔽焊盘的一个常见应用是射频步进衰减器（图 6）。

图6. 示例应用显示了在RF步进衰减器中使用掩蔽焊盘。图片由 侥幸

在上图所示的示例中，步进衰减器在输入和输出端口均配有3 dB掩蔽焊盘，以确保步进衰减器的不同设置表现出恒定的、定义明确的匹配。使用屏蔽垫的主要缺点是衰减器还会降低所需信号的幅度。这可以使所需信号更接近本底噪声。例如，使用单个3 dB衰减器时，给定负载的回波损耗理想地提高了6 dB;但是，前向行波的幅度也降低了3 dB。

也可以使用匹配网络来实现所需的阻抗匹配，而不会显着衰减所需信号。然而，与匹配网络相比，屏蔽焊盘的一个主要优点是屏蔽焊盘可以在指定频率范围内提供平坦的频率响应。例如，低值衰减器在 DC 至 18 GHz 频率范围内的衰减变化可能为 ±0.2 dB。对于通常在窄频率范围内提供阻抗匹配的阻抗匹配网络，情况并非如此。

失配不确定性图

研究失配不确定性如何随Γ变化是有益的1 和Γ2.如图 7 所示，图 7 取自 是德科技应用说明.

图7. 显示不匹配不确定性变化的图。图片由 是德科技 [点击图片放大]

这些图显示了 MU 以 ±dB 为单位的变化。例如，使用Γ1 = Γ2 = 0.05，我们知道失配不确定性约为±0.021 dB，这与上述一组图一致。这里重要的观察结果是，通过将其中一个反射系数足够低，我们可以控制失配不确定性。例如，使用Γ1 = 0.05（对应于1.1的VSWR），即使Γ，失配不确定性仍保持在约±0.2 dB以下2 = 0.5（或驻波比为 3）。例如，考虑RF功率测量应用。如果选择低驻波比的功率传感器，则可以确保根据传感器的驻波比有多低（无论电源的驻波比如何），在一定程度上控制了失配不确定性。 

失配不确定性的统计模型

在上面的讨论中，我们只考虑了失配不确定性的上限和下限。虽然这让我们了解威廉希尔官方网站 中最坏情况下的不确定性，但有一个误差的统计模型是很有用的。我上面提到的是德科技应用笔记总结了针对失配不确定性可以考虑的不同概率密度函数 （PDF）。要查找 MU 的 PDF，请考虑三种不同的发行版Γ1 和Γ2，如图 8 所示。

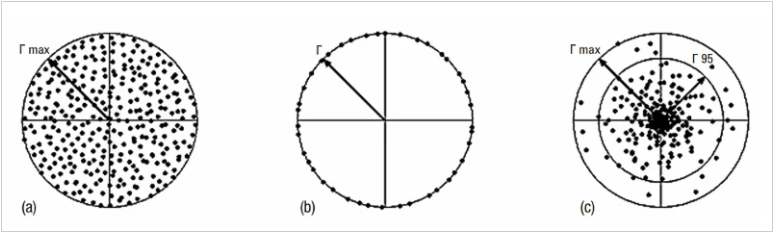
图8. 显示三种不同分布Γ的示例1 和Γ2.图片由 是德科技.

结合这些分布，发现了六种不同的PDF函数来表示失配不确定性。例如，假设两者都Γ1 和Γ2 具有环形分布（图8（b）），MU具有众所周知的U形分布，如图9所示。

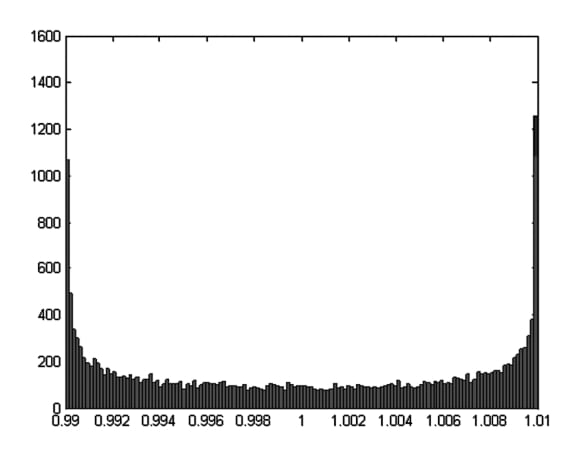
图9. 显示 MU 如何具有 U 形分布的示例图表。图片由 是德科技 [点击图片放大]

这些统计模型使我们能够估计失配不确定性的标准差。有关更多信息，请参阅本文前面链接的是德科技文档。

射频设计和失配不确定性

失配不确定性是设计级联RF模块或进行RF测量时要考虑的重要因素。降低失配不确定性的一种常用方法是将匹配衰减器放置在不匹配阻抗的前面。在处理此错误时，我们有兴趣找到错误的上限和下限及其 PDF 函数，以便我们可以估计错误的标准偏差。