

用Python从头实现一个神经网络来理解神经网络的原理2
电子说
1.3w人已加入
描述
*05 ***** 例子:前馈
我们继续用前面图中的网络,假设每个神经元的权重都是 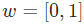 ,截距项也相同
,截距项也相同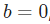 ,激活函数也都是S型函数。分别用
,激活函数也都是S型函数。分别用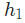 ,
,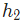 表示相应的神经元的输出。
表示相应的神经元的输出。
当输入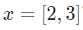 时,会得到什么结果?
时,会得到什么结果?
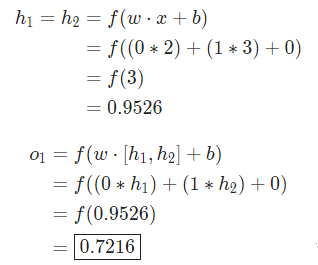
这个神经网络对输入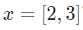 的输出是0.7216,很简单。
的输出是0.7216,很简单。
一个神经网络的层数以及每一层中的神经元数量都是任意的。基本逻辑都一样:输入在神经网络中向前传输,最终得到输出。接下来,我们会继续使用前面的这个网络。
***06 ***编码神经网络:前馈
接下来我们实现这个神经网络的前馈机制,还是这个图:
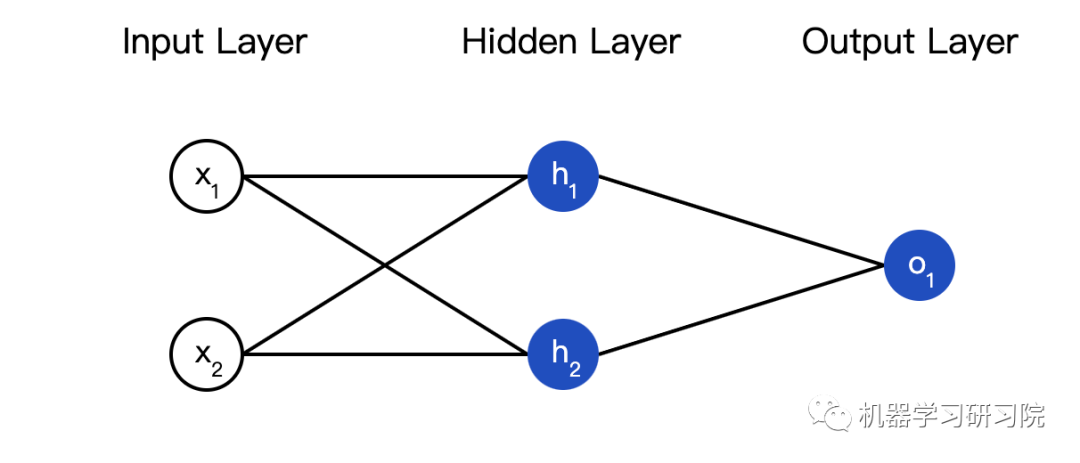
import numpy as np
# ... code from previous section here
classOurNeuralNetwork: ''' A neural network with: - 2 inputs - a hidden layer with 2 neurons (h1, h2) - an output layer with 1 neuron (o1) Each neuron has the same weights and bias: - w = [0, 1] - b = 0 ''' def__init__(self): weights = np.array([0, 1]) bias = 0
# 这里是来自前一节的神经元类 self.h1 = Neuron(weights, bias) self.h2 = Neuron(weights, bias) self.o1 = Neuron(weights, bias)
deffeedforward(self, x): out_h1 = self.h1.feedforward(x) out_h2 = self.h2.feedforward(x)
# o1的输入是h1和h2的输出 out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))
return out_o1
network = OurNeuralNetwork()x = np.array([2, 3])print(network.feedforward(x)) # 0.7216325609518421***07 ***训练神经网络 第一部分
现在有这样的数据:

接下来我们用这个数据来训练神经网络的权重和截距项,从而可以根据身高体重预测性别:
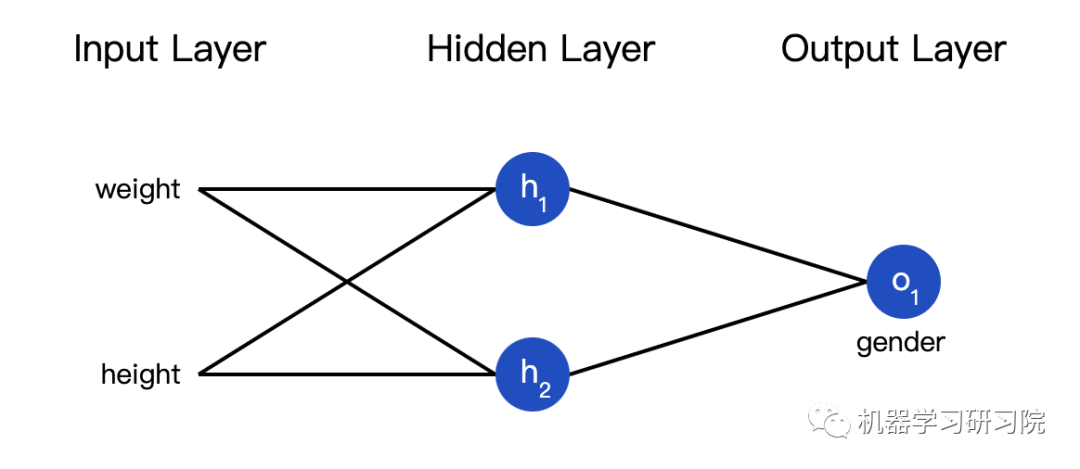
我们用0和1分别表示男性(M)和女性(F),并对数值做了转化:

我这里是随意选取了135和66来标准化数据,通常会使用平均值。
***08 ***损失
在训练网络之前,我们需要量化当前的网络是『好』还是『坏』,从而可以寻找更好的网络。这就是定义损失的目的。
我们在这里用平均方差(MSE)损失: ,让我们仔细看看:
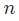 是样品数,这里等于4(Alice、Bob、Charlie和Diana)。
是样品数,这里等于4(Alice、Bob、Charlie和Diana)。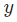 表示要预测的变量,这里是性别。
表示要预测的变量,这里是性别。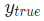 是变量的真实值(『正确答案』)。例如,Alice的
是变量的真实值(『正确答案』)。例如,Alice的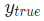 就是1(男性)。
就是1(男性)。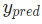 变量的预测值。这就是我们网络的输出。
变量的预测值。这就是我们网络的输出。
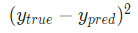 被称为方差(squared error)。我们的损失函数就是所有方差的平均值。预测效果越好,损失就越少。
被称为方差(squared error)。我们的损失函数就是所有方差的平均值。预测效果越好,损失就越少。
更好的预测 = 更少的损失!
训练网络 = 最小化它的损失。
*09 ***** 损失计算例子
假设我们的网络总是输出0,换言之就是认为所有人都是男性。损失如何?
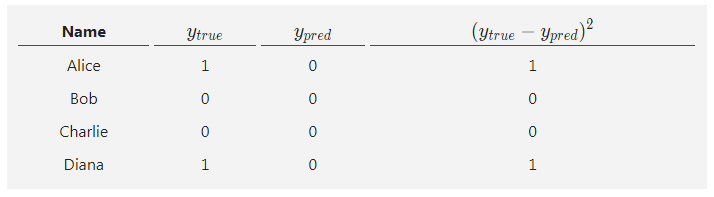
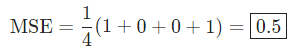
***10 ***代码:MSE损失
下面是计算MSE损失的代码:
import numpy as np
defmse_loss(y_true, y_pred): # y_true and y_pred are numpy arrays of the same length. return ((y_true - y_pred) ** 2).mean()
y_true = np.array([1, 0, 0, 1])y_pred = np.array([0, 0, 0, 0])
print(mse_loss(y_true, y_pred)) # 0.5如果你不理解这段代码,可以看看NumPy的快速入门中关于数组的操作。
好的,继续。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
人工神经网络原理及下载2008-06-19 0
-
labview BP神经网络的实现2017-02-22 0
-
【PYNQ-Z2申请】基于PYNQ-Z2的神经网络图形识别2019-01-09 0
-
【PYNQ-Z2试用体验】神经网络基础知识2019-03-03 0
-
卷积神经网络如何使用2019-07-17 0
-
【案例分享】ART神经网络与SOM神经网络2019-07-21 0
-
人工神经网络实现方法有哪些?2019-08-01 0
-
什么是LSTM神经网络2021-01-28 0
-
如何构建神经网络?2021-07-12 0
-
matlab实现神经网络 精选资料分享2021-08-18 0
-
基于BP神经网络的PID控制2021-09-07 0
-
卷积神经网络一维卷积的处理过程2021-12-23 0
-
用Python从头实现一个神经网络来理解神经网络的原理12023-02-27 699
-
用Python从头实现一个神经网络来理解神经网络的原理32023-02-27 729
-
用Python从头实现一个神经网络来理解神经网络的原理42023-02-27 688
全部0条评论

快来发表一下你的评论吧 !

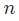 是样品数,这里等于4(Alice、Bob、Charlie和Diana)。
是样品数,这里等于4(Alice、Bob、Charlie和Diana)。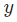 表示要预测的变量,这里是性别。
表示要预测的变量,这里是性别。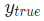 是变量的真实值(『正确答案』)。例如,Alice的
是变量的真实值(『正确答案』)。例如,Alice的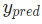 变量的预测值。这就是我们网络的输出。
变量的预测值。这就是我们网络的输出。