

详解矢量的正交分解
描述
矢量的正交分解
1.矢量正交
两矢量V1与V2正交,夹角为90°
两正交矢量的内积为零
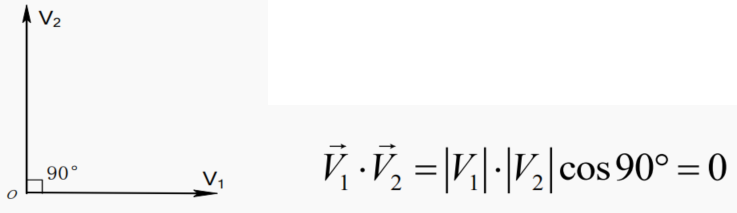
2.正交矢量集:
由两两正交的矢量组成的矢量集合
非正交矢量的近似表示及误差
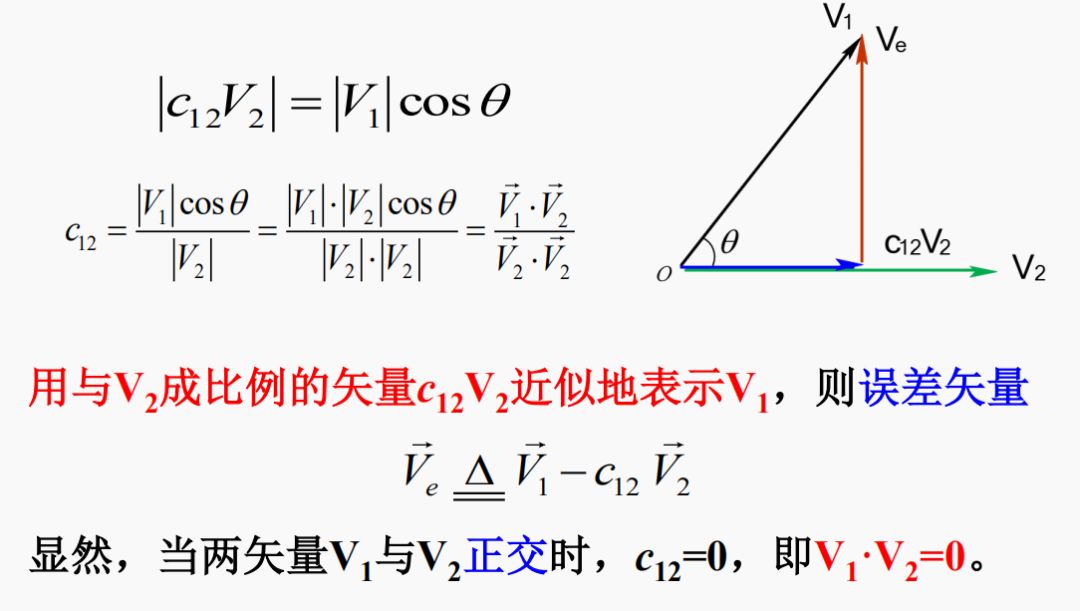
4.矢量正交分解:任意N维矢量可由N维正交坐标系表示
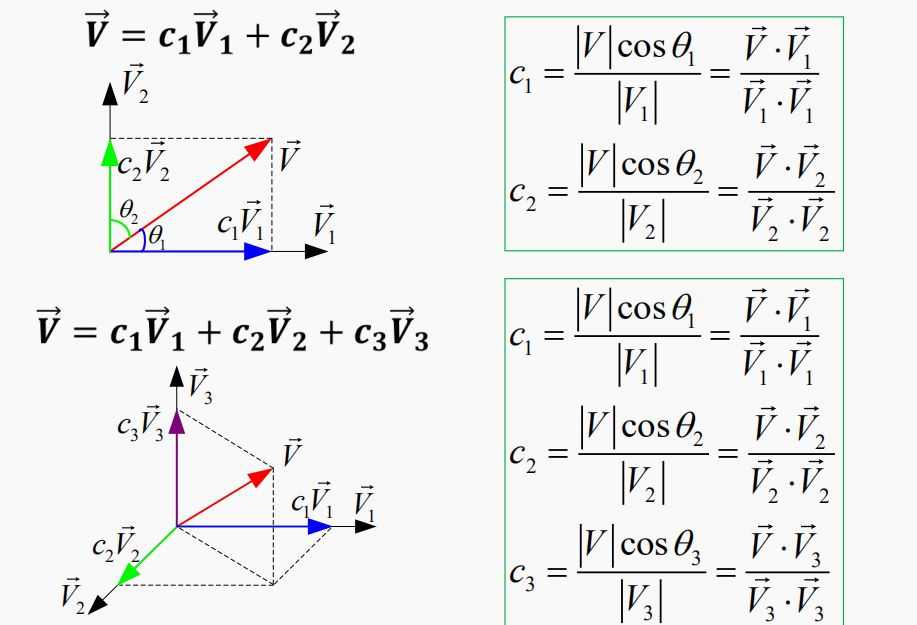
推广到n维空间:n维空间的任一矢量V,可以精确地表示为n个正交矢量的线性组合, 即
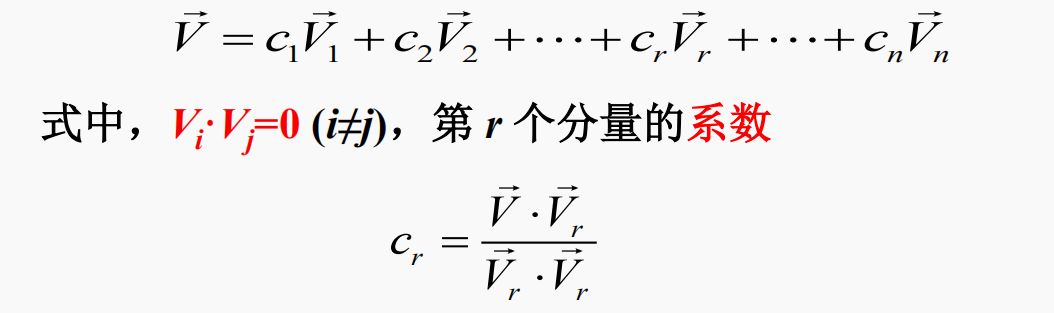
思路:
将矢量空间正交分解的概念可推广到信号空间:在信号空间找到若干个相互正交的信号作为基本信号,使得信号空间中任意信号均可表示成它们的线性组合。
信号的正交分解
1.信号正交
【定义】

说明:实函数正交

2.正交函数集:

说明:如果 Ki=1,称为标准正交函数集。
3.完备正交函数集:

例:两组典型的在区间(t0,t0+T )(T=2π/Ω)上的完备正交函数集
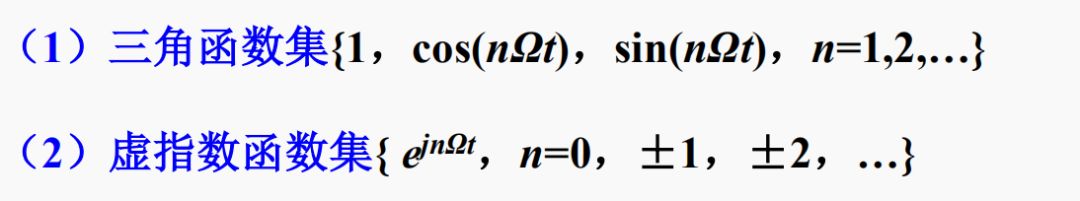
信号的正交分解

如何选择各系数Cj,使f(t)与近似函数之间误差在区间(t1,t2)内为最小?
通常使误差的方均值(称为均方误差)最小。
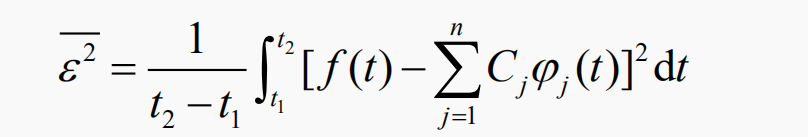
为使上式最小(系数Cj变化时),有
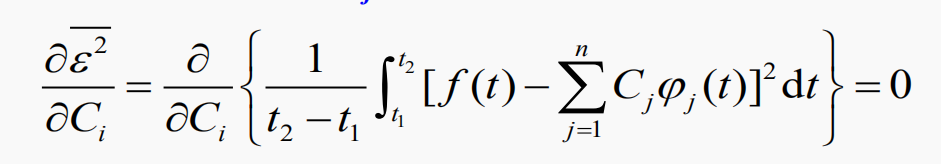
展开被积函数,并求导,只有两项不为0,写为:
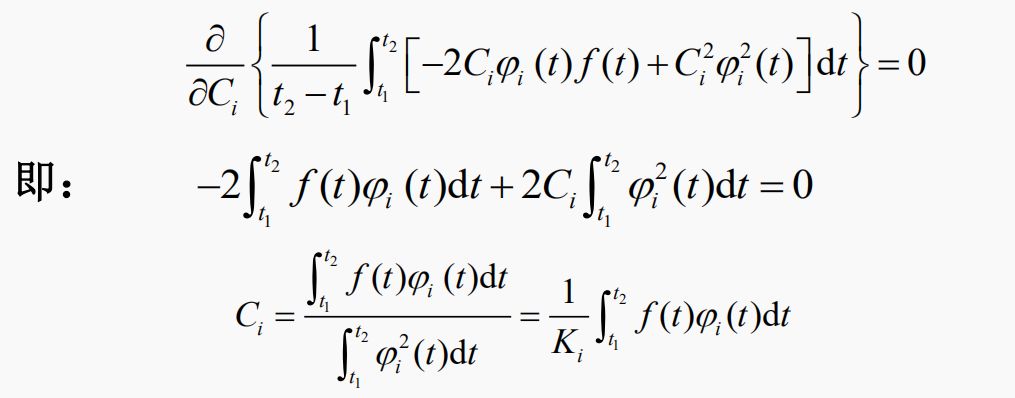
代入,得最小均方误差
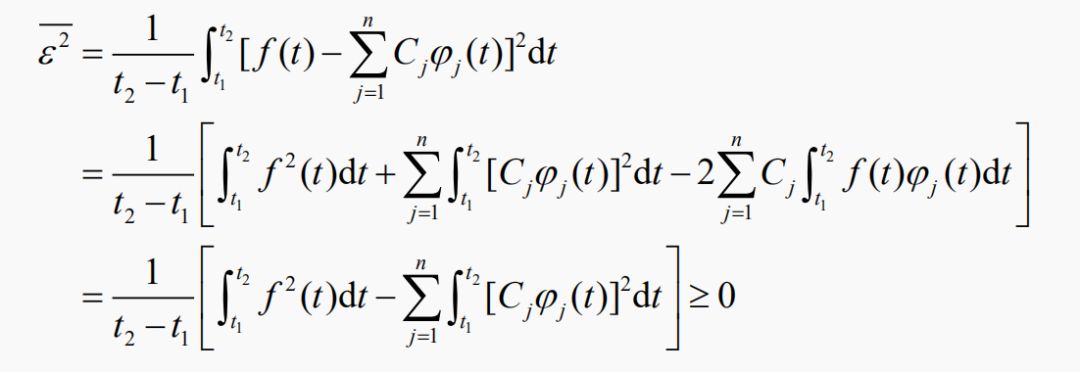
在用正交函数去近似f(t)时,所取的项数越多,即n越大,则均方误差越小。 当n→∞时(完备正交函数集),均方误差为零。
结论:
任意信号f(t)可以表示为无穷多个正交函数之和 :
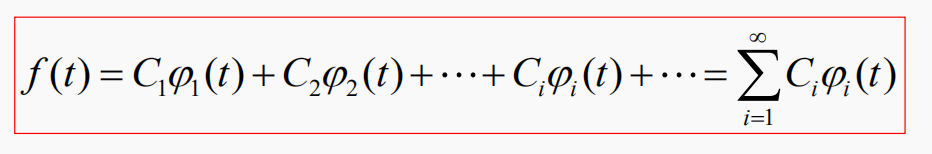
上式称为信号的正交展开式,也称为广义傅里叶级数
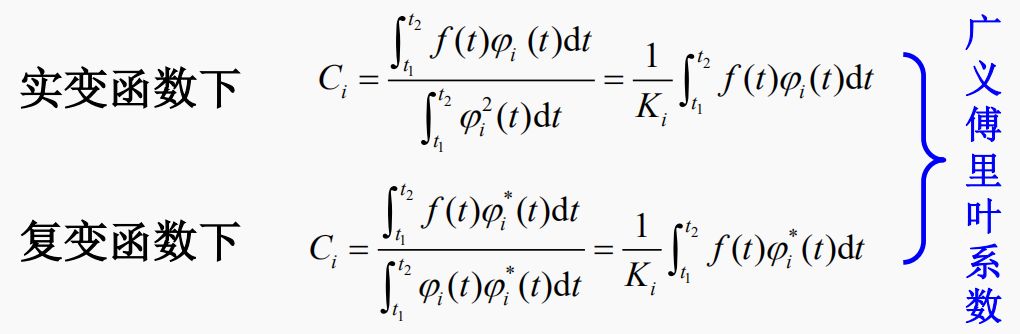
帕斯瓦尔定理
帕斯瓦尔方程:

物理意义:在区间(t1,t2), 信号f(t)所含有的能量恒等于此信号在完备正交函数集中各正交分量能量之和,即能量守恒定理, 也称帕斯瓦尔定理。
数学本质:矢量空间信号正交变换的范数不变性。
-
信号的正交分解和差分传输的区别2018-09-11 0
-
基于CORDIC技术的无开方无除法的MQR阵分解方法2020-11-23 0
-
【原创分享】电机控制中矢量图的作用2021-06-23 0
-
关键基于二维小波变换的图像矢量分解消噪方法2010-08-10 1080
-
电磁波正交极化,电磁波正交极化原理是什么?2010-04-03 11351
-
基于特征矢量稀疏分解的DOA估计方法2017-01-07 724
-
一种信号矢量分解的采样滤波移动节点定位算法2018-02-09 876
-
非正交三维坐标系下多电平空间矢量调制策略2018-04-24 1229
-
矢量控制与V/F控制详解2018-07-24 45992
-
信号的IQ正交分解和差分传输是什么?信号正交分解和差分传输详细概述2018-09-24 10656
-
矩阵的分解教程之满秩方阵的正交和三角分解资料说明2019-11-01 908
-
基于矢量场的二维区域全自动分解方法2021-06-03 634
-
空间电压矢量调制SVPWM技术详解2021-11-22 823
-
连续周期信号的傅里叶分解2022-07-29 3881
全部0条评论

快来发表一下你的评论吧 !

