

开关电源学习笔记
描述
观察点
为了仿真变换器加上补偿网络后的传递函数,可以直接把环路在误差电压处断开,以占空比信号为输入,误差电压为输出,进行交流分析。 所谓的断开,其实可以与之前一样,接入一个大电感和大电容即可。

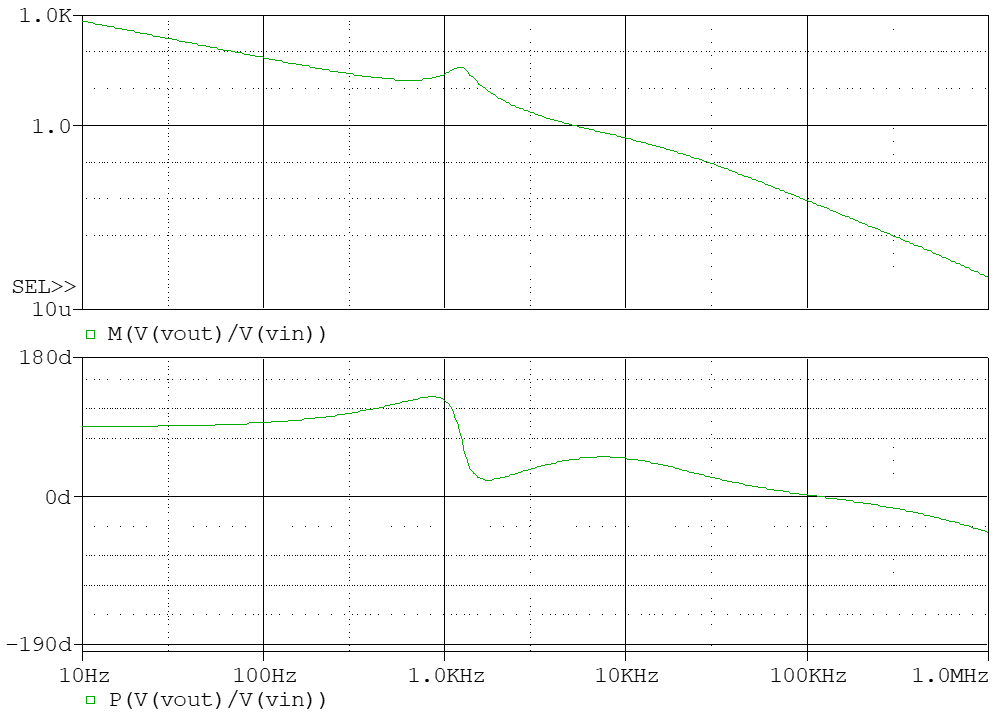
注意这里忽略了放大器引入的相移,因此相位从正的开始,相位裕度以与0°线的距离计算。 可见补偿后的系统相位裕度抬高了。
频域参数
当输出信号和控制信号之间的相位差减少为0°,则变成正反馈振荡器。
交叉频率处的输出容抗可以近似表示闭环输出阻抗,所以可以近似计算出输出瞬态阶跃电流作用下的输出电压脉冲
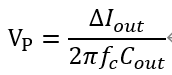
根据这个式子以及稳态纹波需求,可以确定交叉频率的取值。 不过对于有RHPZ的拓扑,一般就直接选定为RHPZ所在频点的30%,同时又应该保证交叉频率在LC谐振频率的5倍以上,给设计带来困扰。 对于没有RHPZ的拓扑,可以直接设定为开关频率的20%以下。 脉冲峰值固然与上式有关,不过恢复时间则由相位裕度决定。
构建补偿网络
构造零极点的知识均已知晓。 值得一提的有构造RHPZ的方法,就是将原输入信号与高通滤波器后的信号相减
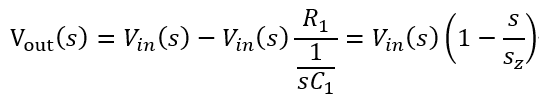
零点频率即RC分之一。
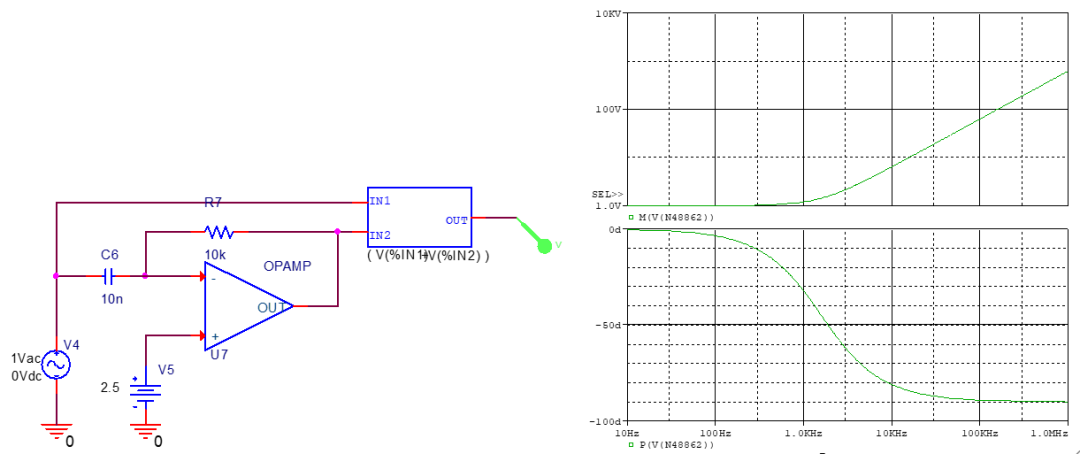
RHPZ是变换器间接能量传输的结果。 在CCM的Boost变换器中表现为,如果负载出现向上的阶跃,造成占空比信号变大,即减小,即电感向负载供电流的周期减小。 但是电感电流不会马上增大,而是以固定步长增加,这个过程中输出电流可能会反而比原来更小,这就是RHPZ的影响。 如果系统响应很快,那么在负载跃变瞬间,反馈环的占空比输出会因为输出电压的反向减小而迅速增大到1,使变换器无法工作,这也是Boost变换器环路设计要降低交越频率的原因。 一般选择在最低RHPZ的1/3处。 DCM时变换器仍存在RHPZ,但其被推到高频处,因此环路设计的困难相应降低。
各个频率响应对应的有源威廉希尔官方网站 网络依次示下:
积分器
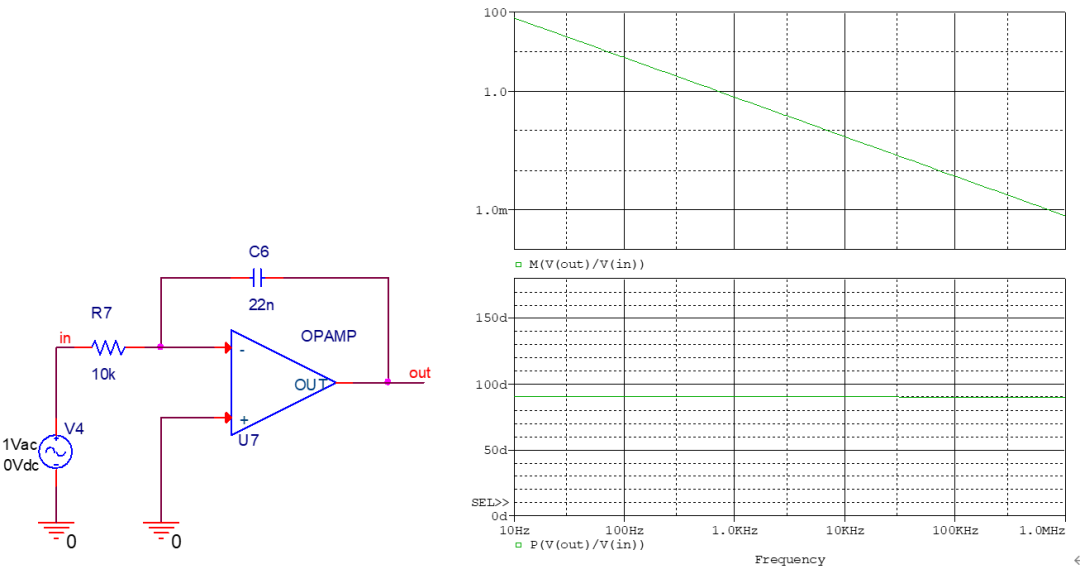
零极点
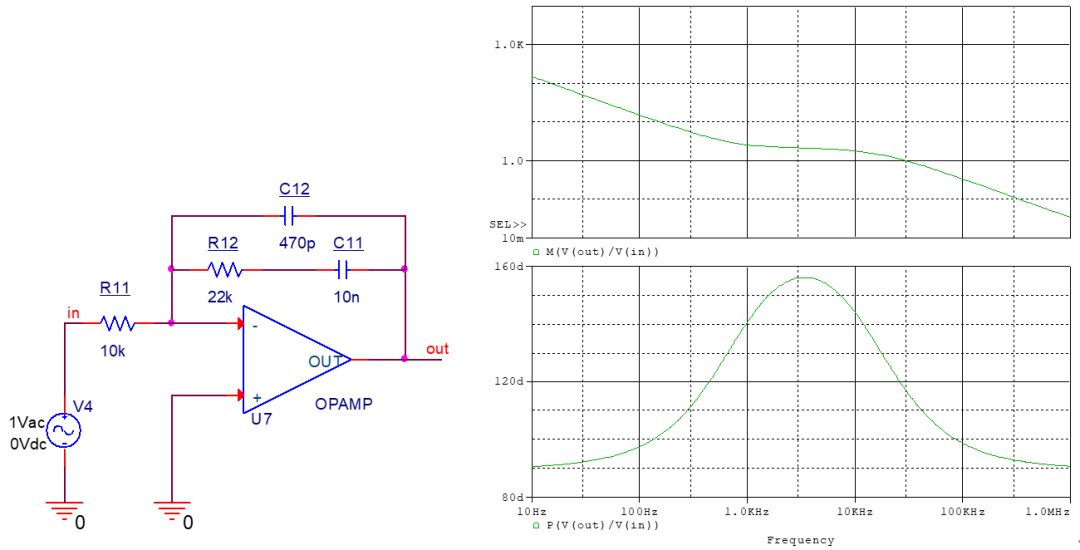
极点位置为
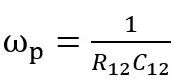
,零点位置为
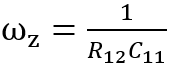
,并且有积分器的效果。 这种补偿网络的特点是中频部分存在一个固定增益区,并且该区域的相位具有超前性质,相位的最大值出现在频率为
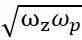
处。 用于电流模式和DCM。
零极点对a
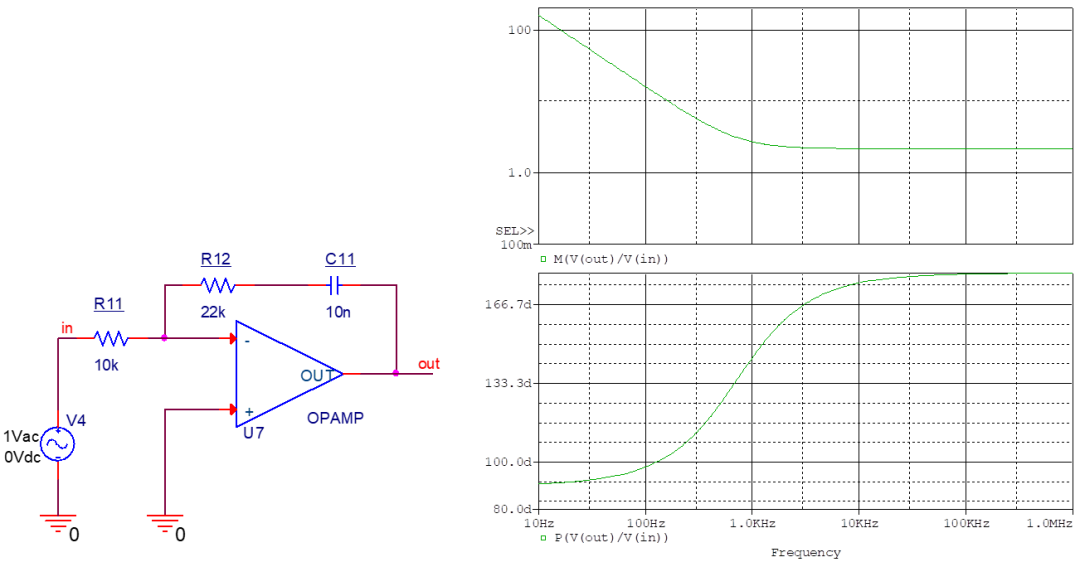
这是上面的特殊情况,即C12为0时,极点被排除,因此不存在高频段的增益下降,相位也一直接近同相。 在无需考虑ESR零点的场合可以用这个简化的补偿器。
零极点对b
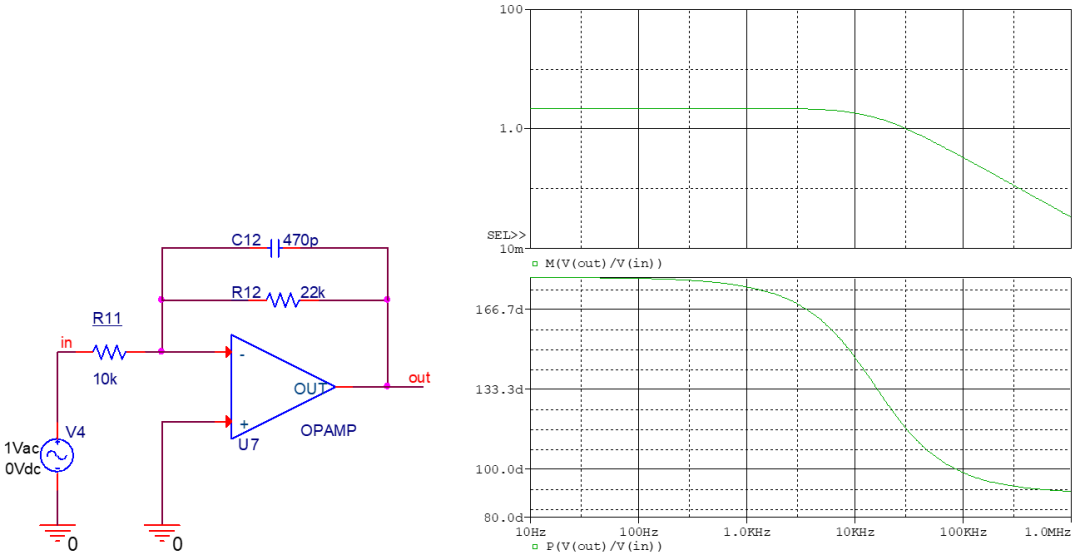
这也是上面的特殊情况,令C11为无穷大,则变成一个原点处的零点,相当于与积分器的效果相抵消,因此低频至中频都为固定增益。 明显的缺点是直流增益太低,稳态精度无法保证。
两个零极点对
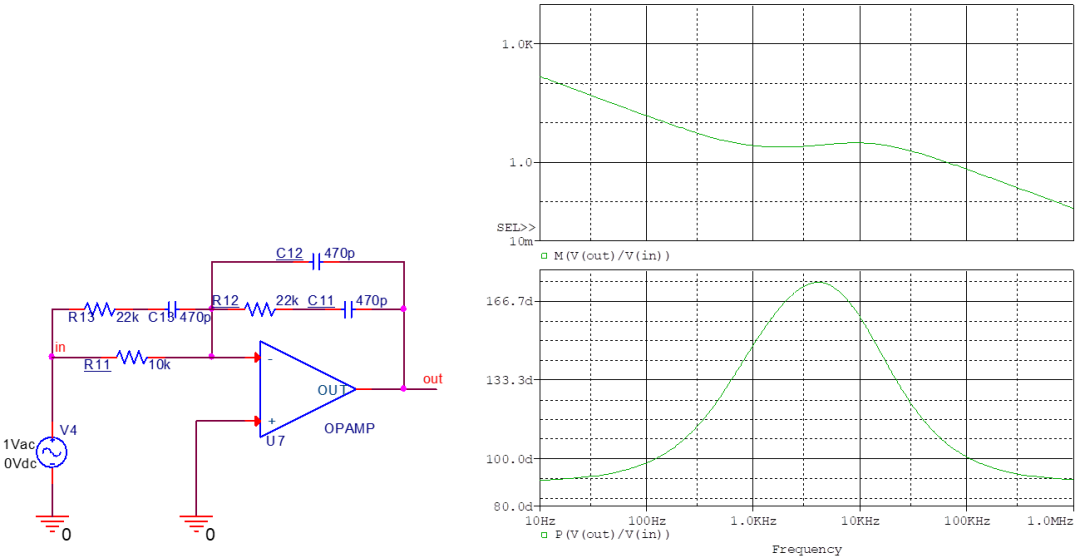
传递函数为
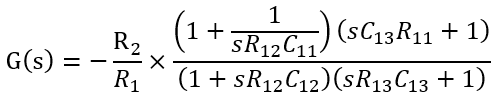
式中就可以看出零极点位置和直流增益。 比起单个的零极点对,两个零极点对提供了更大的直流增益和更大的超前相角,因此是最完备的一种补偿网络。
注意,实际的运算放大器必定自身附带一个低频的极点,其本身的增益就随频率的增大而减小,所以实际设计时还需要根据具体的运放进行参数设计。
K因子
一种从变换器开环特性得到k因子等参数值后,直接推导各类型补偿网络组件参数的方法。
首先看各类型补偿网络需要考虑的补偿参数。
积分器:极点在原点处,所以它只能通过平移增益曲线,改变系统的交叉频率,并引入一个90°的相移。
零极点对:除了具有积分器的平移曲线的效果外,还引入了一个超前相位,某点引入的相位增加量计算为
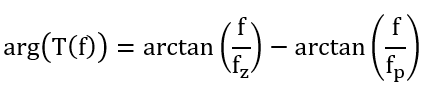
因此在交叉频率处,用k因子的方法可以令极点频率为kf,零点频率为k分之一f,则相位增加量

解出
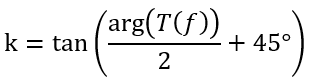
根据所需要的相位裕度和变换器本身的相移,加上积分器引入的90°相移来确定
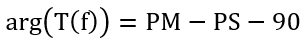
书中给出了不同k值下该补偿器的响应,k=1时退化为积分器,随着k增大,零极点距离增大,超前的相位增大,而直流增益减小。
双零极点对:与上面相似,这里假设双零点重叠,双极点也重叠,那么令极点频率为倍的f,则
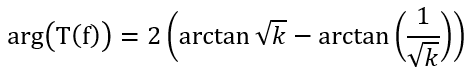
解出
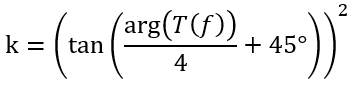
接下来的式子和关系与上述一致。
K因子设计步骤
1、获得变换器交流响应。
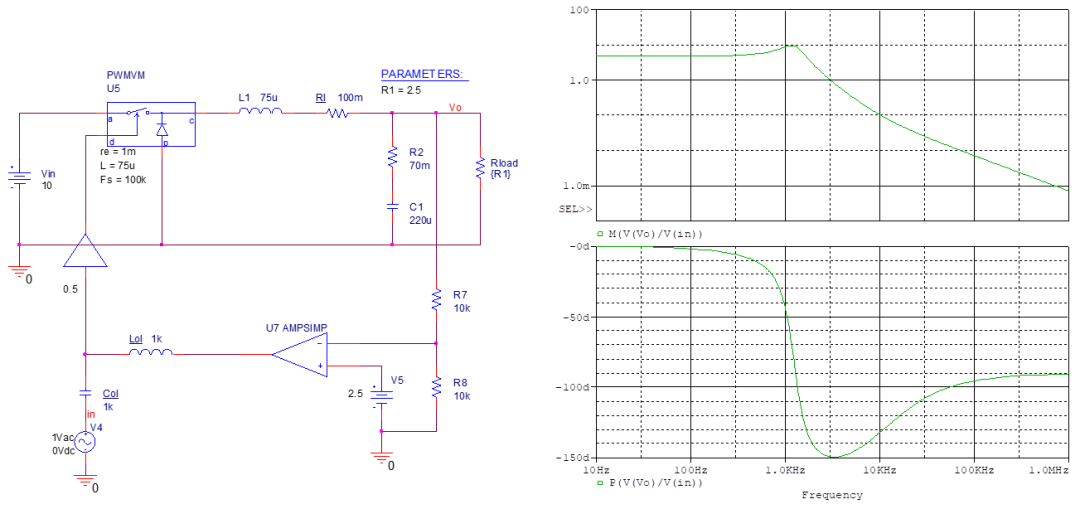
用游标看出交叉频率为3kHz,相移149°。
2、选择交叉频率和裕度。
开关频率为100kHz,而LC峰值频率为
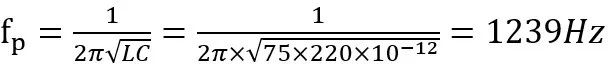
如前所述应该选取6k以上的交叉频率,但是书中选取了5k,先按书中选取,后面再观察不同。
若选取5k,先观察变换器响应中5k处的数据,得到相移为-146°,增益为-9.2dB,期望的相位裕度为45°。
3、选择补偿器类型。
可见到变换器的响应相位滞后达到180°,稳妥起见可以选择双零极点对补偿器,最高可以补偿180°超前相位。
4、应用公式计算组件。
运用上页的公式,计算出k因子和元件参数
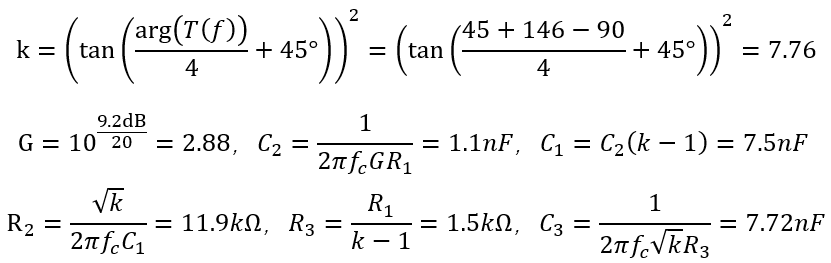
顺便可以计算出补偿器提供的零点和极点频率分别为1.8k和14k。
5、连接补偿器后开环扫描。
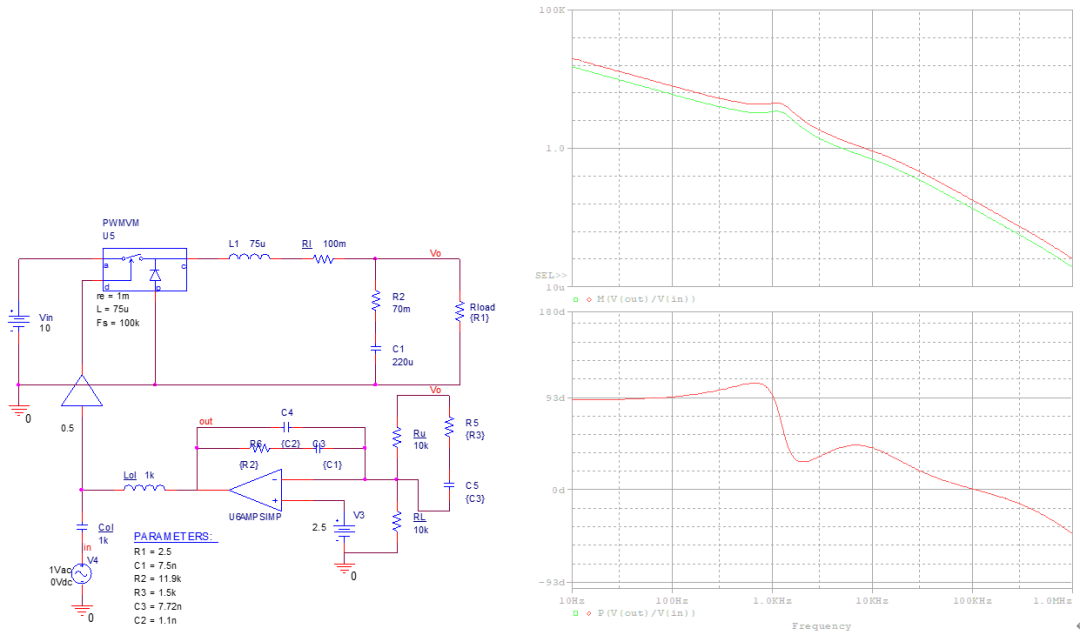
标准输入并带满载情况下的开环响应,交叉频率为5kHz,相位裕度为43°。 变化输入电压为20V,即图中红线所示,环路增益增加了1倍,即曲线被抬高了3dB,因此交叉频率变为8.45kHz,相位裕度为44°。
6、变化ESR和负载检查相位裕度。
以上测得是负载电阻为2.5Ω即电流为2A时的响应,若增大电阻至进入DCM模式,观察补偿器的功能是否受影响。 下图看出,因为变换器在低频处退化为一阶系统,低频段增益减小,所以交叉频率明显降低,分别为613Hz和1kHz,相位裕度分别为39.5°和59.5°,在不同输入电压下的相位裕度相差更大了,即对输入电压更加敏感。
如果变化电容的ESR,道理相同,负载恢复满载情况,若取值变为200m时如下图,交叉频率变为7.83kHz和15.56kHz,相位裕度变为74°和55°。 可见ESR的增大会使得其零点提前出现,使得交叉频率后移,并且提高中频段的相位。
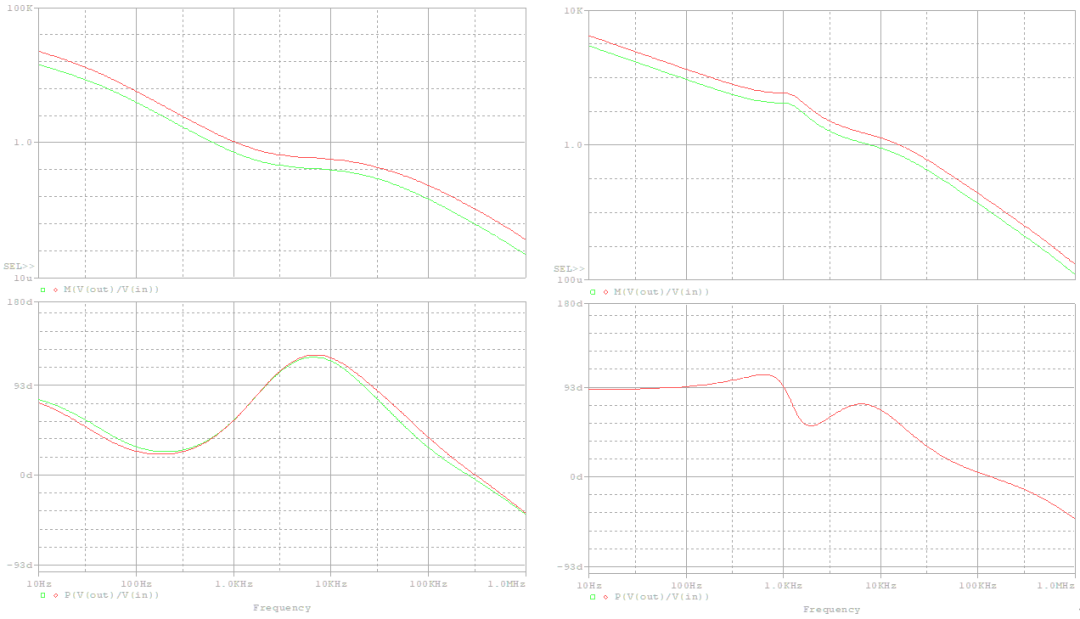
负载为50Ω时 ESR为200m时
7、观察瞬态响应。
前面给出了一个近似估计电流上升阶跃下,电压响应尖峰的计算式
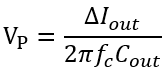
如果作0.1A到2A的阶跃,大致算出峰值为
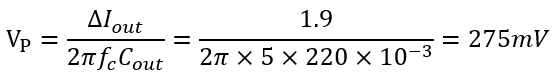
即从5V下降到4.725V。 搭建仿真模型,用ABM+脉冲信号源实现负载切换,结果如下
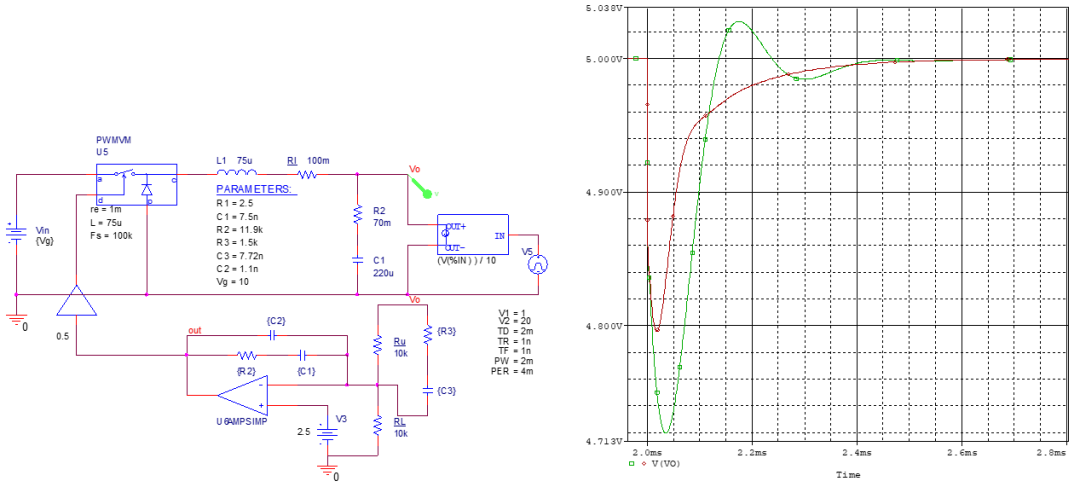
电压跌落为4.713V,与计算值近似相等,误差可能来自ESR等。 书中给出该式,只说明用来计算欠脉冲,若用来计算电流下降阶跃下的电压超调,则似乎不符合仿真结果的5.24V。
下图给出了全貌,明显,DCM下到CCM的切换很快,建立时间大约0.4ms,而DCM切换到CCM则很慢,需要大约5ms。
图中同样以红线示出了20V输入电压下的瞬态响应,说明Buck变换器中确实是以最低输入电压为最恶劣条件,而高输入电压下具有更好的动态性能。
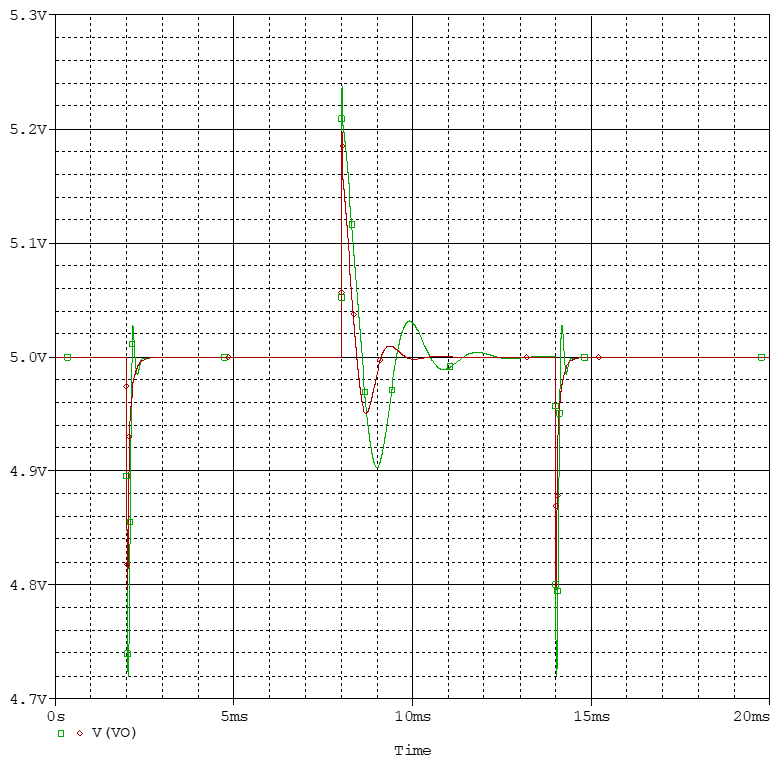
除了输出电压响应外,还应观察误差电压的瞬态响应,这才是变换器在控制意义上的输出。
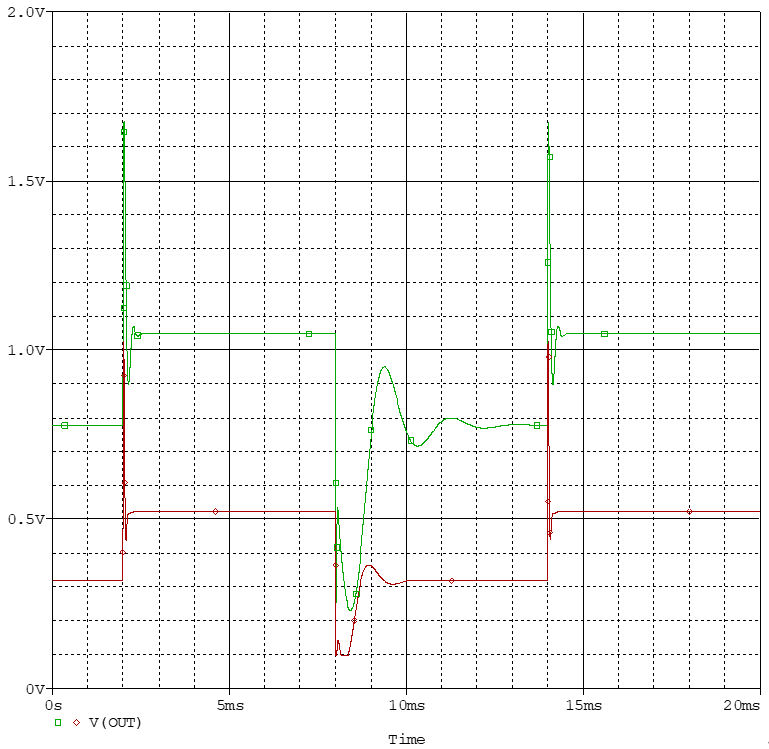
书中到后面也说明了当交叉频率为8kHz时,响应峰值降低为171mV,系统性能应是有所改善。 重复上述步骤,8k处的曲线数据为相移137°,增益-16.5dB,同样选择45°裕度,双零极点对补偿器,列式如下。
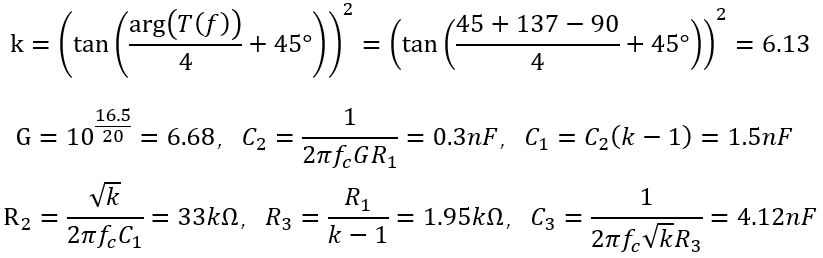
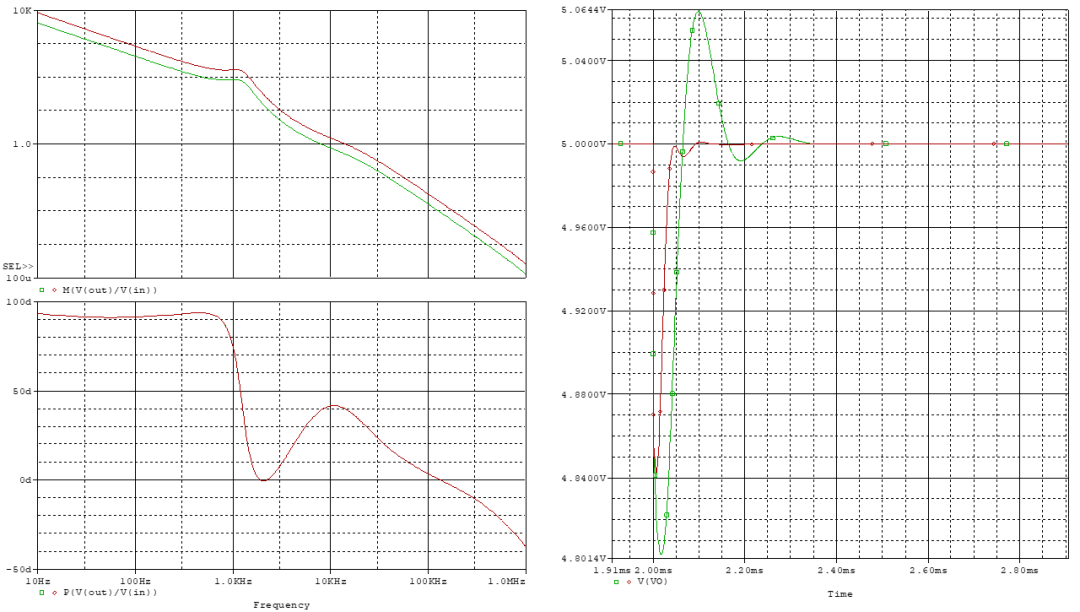
得到曲线如上,与前述相同,用输入电压分别为10V和20V时进行对比,10V时,交叉频率为7.98kHz,相位裕度为42°。 再观察瞬态响应,理论计算的峰值应为,图中为4.8V左右,相差不大,说明该估计式具有足够的精确度。 仔细观察上图中的相位曲线,可以看出一些问题。
K因子法的缺陷
该方法虽然简单,它对响应曲线形状忽略不计,即忽略了可能存在的谐振峰,而只考虑交叉频率。 这样有可能在交叉频率之前出现相位裕度减小到0的情况,如上图所示。 在交叉频率较高为8k时,出现了相位降低到0,增益仍为10以上的情况,这样在该频点很容易就有振荡现象,称为条件稳定。 这种问题出现的原因是K因子法在放置零极点时只考虑交叉频率的实现,而并未考虑零点位置与LC极点位置大致重叠这一要求,所以就会出现无法抵消LC极点引起相移的问题。 所以K因子法好虽好,若要妥善设计,还是应该采取一般的零极点放置法进行配置。
这种一般的方法,精确放置了每一个零极点,可以制作专用的计算表格。 书中提供了一种利用仿真软件进行参数计算的图纸,似乎只能用Ispice,Pspice尚不知可否。
用放置零极点的方法,就不会出现条件稳定性的问题了,图如下,相位裕度为36°。 这种方法的缺陷也正是K因子法的优点,即交叉频率无法精确定位; 另外,书中的理论和实验也表明,K因子法放置的零点频率较高,瞬态响应也会快于放置零极点的方法。 所以各存利弊。
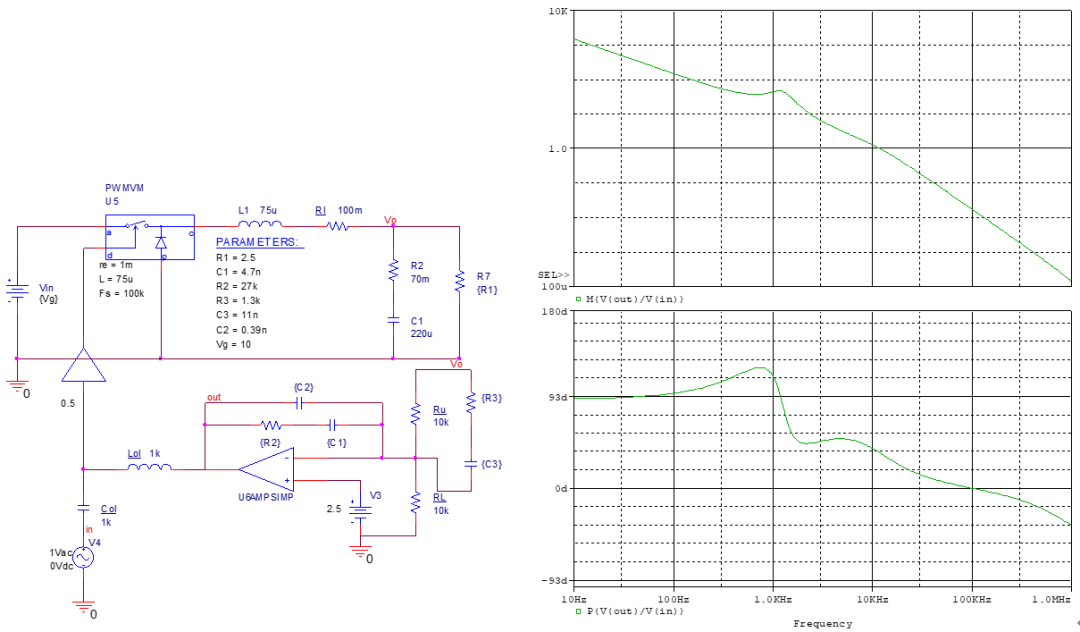
电流模式补偿网络
以上讨论的内容均针对二阶的电压模式Buck威廉希尔官方网站 。 对于电流模式控制来说,变换器的模型在低频呈现为一阶系统。
回顾一下电流模式控制的相关设置。 为避免次谐波振荡,需要加入斜坡补偿,在输入电压为10V时,威廉希尔官方网站 中电感电流的上升和下降斜率一样都为66mA/μs,补偿斜率可以为其一半。 若采集电阻阻值为0.4Ω,则补偿斜坡电压为13.3kV/s。
同样运用K因子法,选择交叉频率为10kHz,相位裕度为80°。 先观察开环曲线。
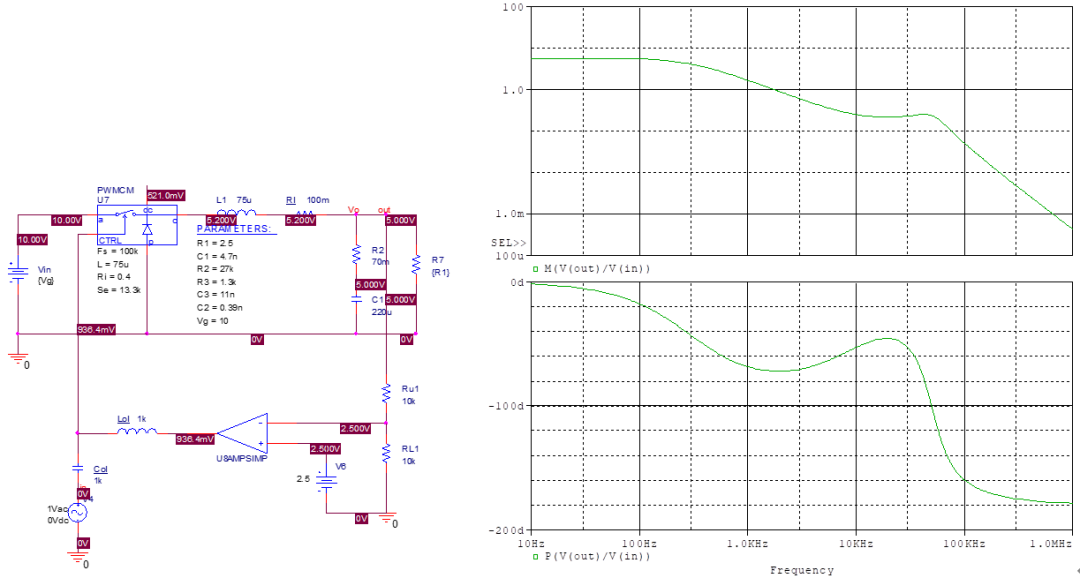
得到10kHz处相位为-52°,增益为0.25=>-12dB。 因为相位滞后在90°以内,可以用零极点对的补偿器(2型)。
计算式如下
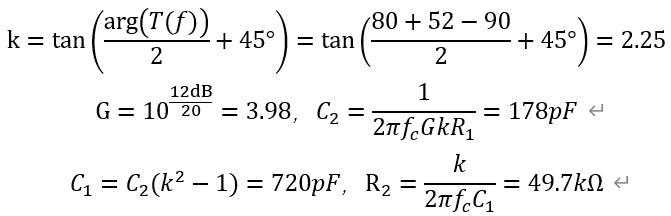
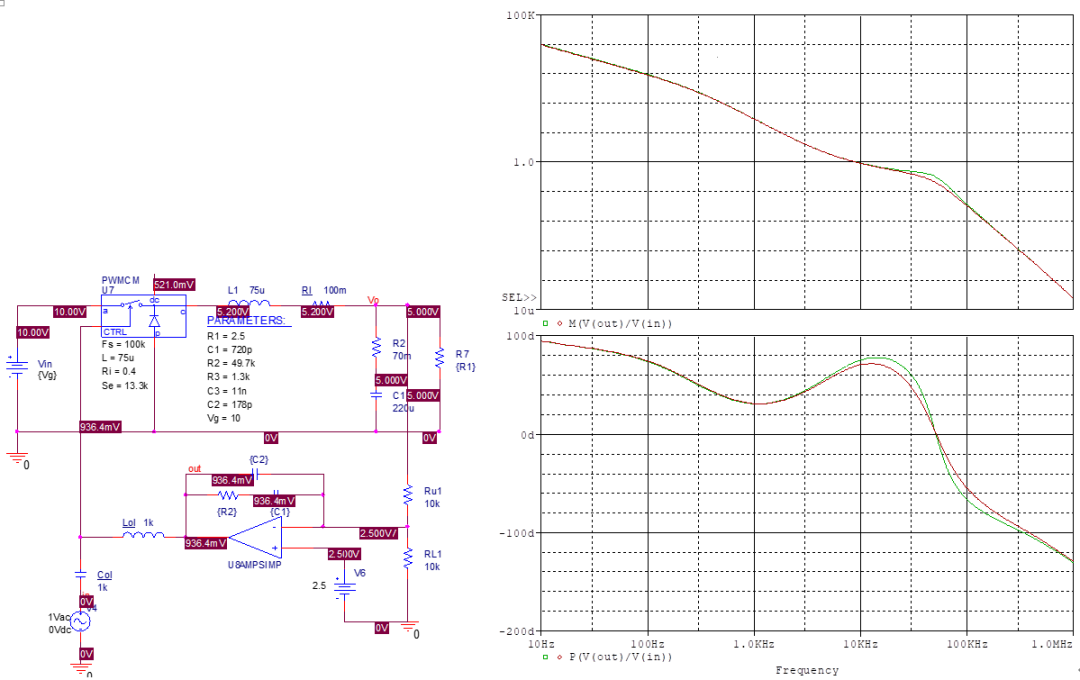
得到补偿后的特性曲线如图。 交叉频率为9.1kHz,相位裕度74°。 值得注意的是在输入电压分别为10V和20V时,两条曲线几乎重合,这是因为电流模式控制下,理论上的音频敏感度就是0,即输入电压的变化不会对系统造成影响。 略去了负载阶跃测试,因为可知道电流模式控制下系统在低频变为一阶系统,自然在阶跃作用下是不会产生振荡的,但峰值电压由输出电容决定,对电压模式和电流模式都是一样的。
此例可以看出K因子法对电流模式的设计还是很有优势的,因为一阶系统的特点,系统本身的相移就不大,所以不会出现条件稳定性的问题。
实际设计之TL431反馈
实际工业应用中已经很少用运算放大器设计补偿威廉希尔官方网站 ,而是将其与基准源合二为一,利用TL431内部的集成误差放大器就可以设计出高性能的补偿威廉希尔官方网站 。 TL431的参考电压为2.5V,TLV431为1.24V,且电流更小。
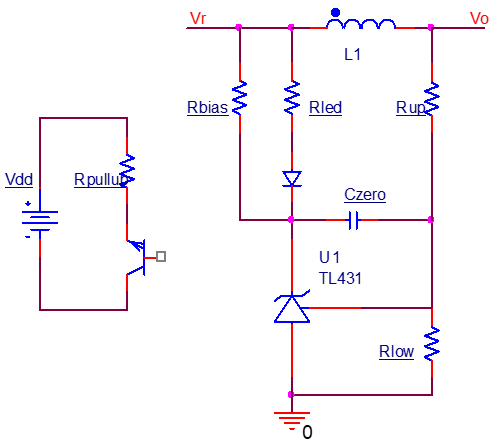
在一般的反馈环路中,连接光耦LED的支路为快支路,分压网络为慢支路,如图所示。 对于小信号的研究,由于TL431的动态电阻与Rled比起来小得多,忽略后由KVL得
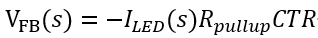
VFB为最终反馈回到芯片FB引脚的电压。
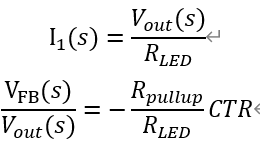
就得到了快通道的传递增益,在高频区难以降低,使放置零点成为一个问题。
整个反馈可以看作快慢通道的叠加,与慢通道叠加后,推导反馈环路的传递函数
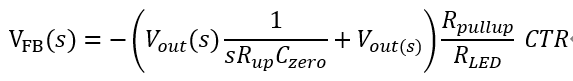
即
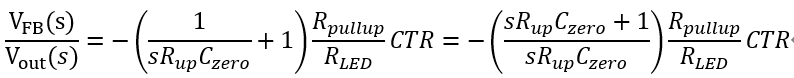
表明了系统中存在原点处极点和一个零点。
必须要明白的一点是,这个威廉希尔官方网站 是实现前面所述补偿网络的方法。 对比零极点对补偿网络,还缺少一个非原点处的极点,可以直接在光耦的输出与地之间接入电容。 得到的零极点位置分别为
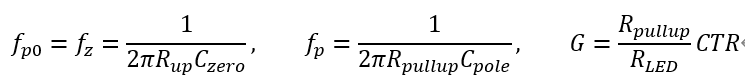
注意到第一条式子的关系,所以曲线的斜率刚好在0dB处发生转折,结果就是中频增益G与零极点位置无关。
下面用TL431实际设计补偿器。
K因子+431
用k因子法直接把零极点放置在
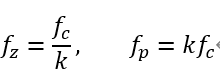
构造零极点对的补偿器做法较为简单,基本上与前述的一般方法一致,直接代入计算即可,得到的响应与前面用运放搭建的结果是一致的。
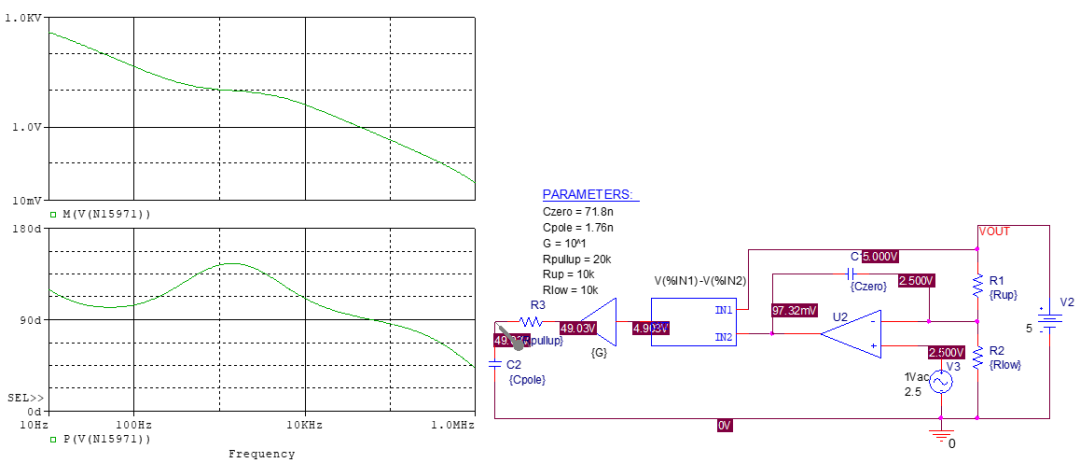
如果搭建双零极点对补偿器,则需要考虑快通道的影响,即高频区存在的增益,它使得直接在上位反馈电阻并联零点的做法没有作用。 因此需要在快通道的LED电阻直接并联RC网络,并联后,原本LED电阻的位置上阻抗变为
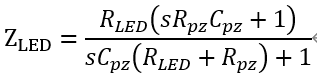
完整的传函变成
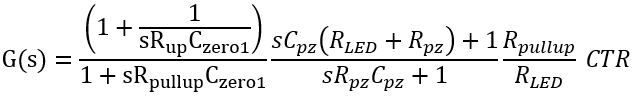
可得到两对零极点的位置。 如果零点和极点的位置都重合,可以求出
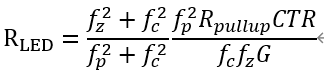
G为期望的交叉频率处增益。 之后就可以根据零极点位置求出RPZ和CPZ的值。
一般不会用TL431搭建这种补偿器,因为LED电阻对零极点位置存在影响,还是用运放搭建较好。
TL431偏置电流
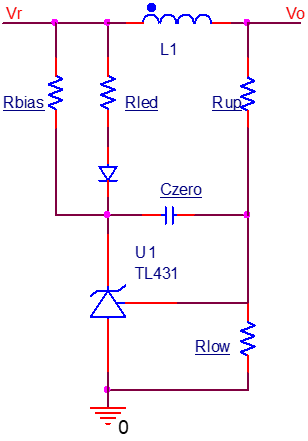
431需要一个从阴极流入的电流满足要求,必须大于1mA,否则其开环增益会大大减小,使稳压效果变差。 一般不能依靠LED电阻提供的电流,因为光耦的CTR会使期望的电流衰减,最后不能达到1mA的要求,所以应该另外增加偏置电阻,通过输出电压直接拉一个电阻到TL431阴极,或者在LED两端并联一个电阻都是可行的。
在仅仅靠LED电流提供偏置时,要考虑最大的光耦传输比。 先计算光耦输出端需要的电流值为
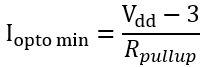
其中Vdd为控制器的逻辑电平,3V是假定反馈引脚的电压上限值。 则LED的电流最小可能是
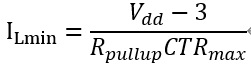
假设Vdd=5V,上拉电阻10k,CTR最大为100%,此时电流200μA,不满足要求。 所以要加入偏置,由最小电流要求得到偏置电阻的取值
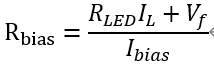
其中Vf为LED的压降,典型值为1V。 若要求偏置电流2mA,LED电阻2.2k,Vdd=4.8V,CTR取典型值为30%,得到偏置电阻为830Ω。
此外还有一个地方的偏置电流需要注意,即从电阻分压过来的电流,进入TL431的参考节点。 进入该节点的电流数据表给出为2~4μA,据此可以计算低端电阻值
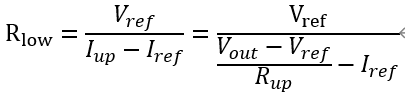
不过如果选择高端电阻的电流远大于μA级别,比如为1mA,就可以忽略这个电流值了。 对于低功耗应用来说,还是应当设定为更低的电流值,这时需要考虑这个电流的限制。
关于光耦
光耦的输出端中,集电极和基极之间存在较大的电容,会影响可用带宽,此带宽由电容和上拉电阻共同决定。 从数据表中给出的下降时间和测试电阻值可以计算出结电容值
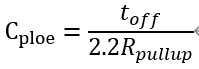
一般为nF级别。 因此对要求较大带宽的电源,光耦会造成较大的影响,或者使用阻值很小的上拉电阻。
另外,光耦还存在着一个高频的极点。
跨导放大器
输出电流为两个输入电压差的倍数。 特别之处在于跨导放大器不存在局部反馈,相当于开环运行,输入端也没有虚地的情况,而且分压电阻的下位电阻在环路中起作用。 常在PFC中应用。
-
.基本DC-DC变换器开关电源学习笔记2021-10-29 0
-
大佬都在看的开关电源学习笔记2021-10-29 0
-
开关电源学习笔记2012-06-16 491
-
开关电源学习笔记0 --- 初识开关电源2021-10-22 944
-
开关电源学习笔记 --- 目录2021-10-22 994
-
开关电源学习笔记1 --- Buck变换器的基本原理2021-10-22 712
-
开关电源学习笔记2 --- Boost变换器的基本原理2021-10-22 505
-
开关电源学习笔记3 --- Buck-Boost变换器的基本原理2021-10-22 921
-
开关电源学习笔记8 --- Cuk变换器2021-10-22 913
-
开关电源学习笔记7 --- DC-DC变换器的储能电感设计之磁芯及气隙2021-10-22 622
-
开关电源学习笔记9 --- SPEIC变换器2021-11-07 401
-
开关电源学习笔记10 --- Zeta变换器2021-11-07 445
-
开关电源学习笔记之MOS管2022-01-11 617
全部0条评论

快来发表一下你的评论吧 !

