强攻磁性原子链的马约拉纳简析

 在我们大众的学习记忆和印象中，物理学规律总是那么简明、直接、铿锵有力而不可撼动！对视觉结构敏感的人们，还会觉得物理学规律的表达美观、对称，堪称天工物语。这些记忆一定程度上都源于客观事实，所以才有“The tenequations that rule the world”和“The seven equations that rule yourworld”之类的众说纷纭。这些 equations 方程中，与物理相关的，都是最能体现“严谨性”和“主导性”的杰出作品。说严谨性，是指将物理状态或过程用假设的理想条件 (这些条件基本上都是合理和似乎可及的) 约束起来，而将复杂性放置入比例系数中，以突出要渲染的物理很简洁明锐、一丝不苟。说主导性，则与过去数百年来物理研究的传统有关，乃指存在某个“一览众山小”的物态或过程，它主导了好的物理。而那些枝节和旁门，都可被适当地舍弃，不会影响物理的因果。

正因为如此，才有物理规律“神一般”的存在，并引导一代一代志向高远的人们进入到物理学围城。Ising 不过是物理世界的一粒尘埃，但同样能感受到其中的艰辛与乐趣。早年，Ising 在最需要感性经验和教训失败累积的学科 — 铸造专业中学习时，就是被 1980 年代前后发展出来的枝晶凝固理论所吸引 (该理论算得上是这一专业为数不多的高雅物理)，从而决定转到凝聚态物理学科。那时候，我们笃信，素雅雪花或钢铁洪流中复杂的凝固过程，就是由这方小小的枝晶尖端决定的，如图 1(A) 所示。现在的我们知道，那单一、可控的枝晶尖端所拥有的“曲率半径的平方 × 生长速率 = 常数”的选择原理，也许对理解枝晶形成有价值。但是，钢铁洪流未必遵从这一原理，或者说这一原理未必就是主导枝晶之手：钢铁洪流中能掩盖这一原理的复杂性环节，实在是太多了。

这些复杂性，还在继续上演。大学《电磁学》课程中，第三章一般讲授电介质。描述电介质的物理，可以由电感应强度 D = ε0 E + P 来表达。这里的 E 和 P，是电场和电极化，其中极化 P 蕴含了电介质无尽的复杂性。麦克斯韦方程组不管这些复杂性，而是很轻松地将 D 纳入其中，将复杂性隐藏起来，如图 1(B) 所示，害得如 Ising 之辈在电介质领域瞎逛数十年而不得要领。当然，如果在某一领域内长时间到处瞎逛，也并非就毫无收获，有时候也能见到诸多新环境中诞生与成长起来的树木和森林。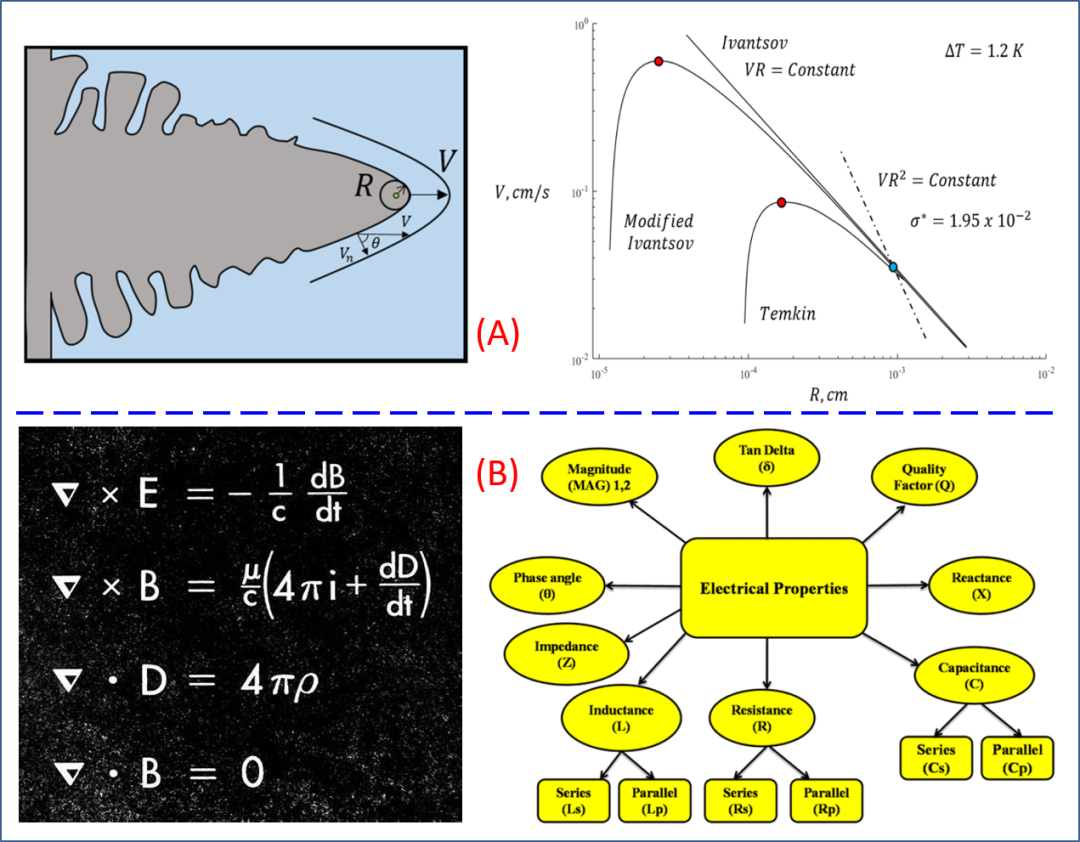

 

图 1. 材料科学中复杂性的两个例子：(A) 金属合金凝固时枝晶尖端的形态及其选择原理。其中尖端曲率半径 R 和生长速率 V 之间的关系满足 R2V = constant。(B) 电介质物理中电极化的电磁学。左边所示是麦克斯韦方程组，右边则列举电介质物理的复杂性元素。

量子材料，就是在这样的环境中成长起来的大片森林，并引得山川蜿蜒、春秋各异。从一个视角去看，这些森林与传统物理园地的主要差别，就在能量尺度上。相比传统物理过程，量子材料涉及的能量尺度大为降低，因此经典物理常见的主导性很强的规律特征在量子材料这里就变得模糊不清。很多原本被忽略、被线性化舍弃的复杂因素，开始显山露水而不甘于被轻视忽略。原本被忽略的复杂性，在量子材料这里很常见，并成为量子凝聚态必须面对的大问题。图 2 给出量子材料森林中的一些树木，个中形态都较为复杂。

面对如此态势，量子材料研究遭遇了多方面的挑战。这里姑且两个层面提及一二。

首先，理论处理一个体系的标准策略，是构建一个简化版的模型，去抓取其中主要的物理元素。这一策略的前提条件是，体系中各种相互作用总是主次分明、轻重迥异的。遗憾的是，这样的主次高低和轻重缓急在量子材料中并不那么分明，简化的模型就会因此丧失掉很多好物理。传统固体物理先求基态、再染指低能激发态的逻辑，在量子材料这里遇到挑战。面对这一窘境，物理人的应对之法大概分为三类：(1) 第一类应对，便是如 Alexei Kitaev 教授这样的高人出手，构建出高度凝练的物理模型，并获得严格解。这样的例子凤毛麟角，总是难以为继的。(2) 第二类应对，便是较为现代的技法，即诉诸人工智能、机器学习这样的先进手段，将困难扔给机器去寻找解决之法。(3) 最后一类应对，便是构建一类完备的模型架构，试图包罗万象，将所有这些复杂性都装进来，然后“硬上蛮干”。

其次，实验研究的逻辑是，激励一个物理进程，并探测其后果，借此解构机制与效应之间的因果关系，为后续操控和性能革新提供技术支撑。事实是，很多情况下这样的实验设计存在问题。果若应用到量子材料中，面对的结果经常是多个能量近似的进程耦合在一起，给实验提取所追求的数据带来复杂性。我们面对一堆数据而一筹莫展，是经常出现的局面。这样的局面，在经典物理中当然也存在。但是，经过对实验条件的优化及纯化，经典物理有机会构建一个“低维化”的实验环境，将主导性因素凸显出来，从而轻松到达彼岸。这里的“低维化”，不是指材料体系的空间低维，而是指物理因果关系的低维化、简单化，以避免诸多物理因果关系纠缠耦合在一起。遗憾的是，在量子材料这里，低维化似乎难以做到，因为实验可操控的参数空间已经是高维。结果是，我们只能看到物理过程的“混沌”特征，只能看到物理结果的 strange attractor 特征。这些，都是量子材料研究的常态。

   

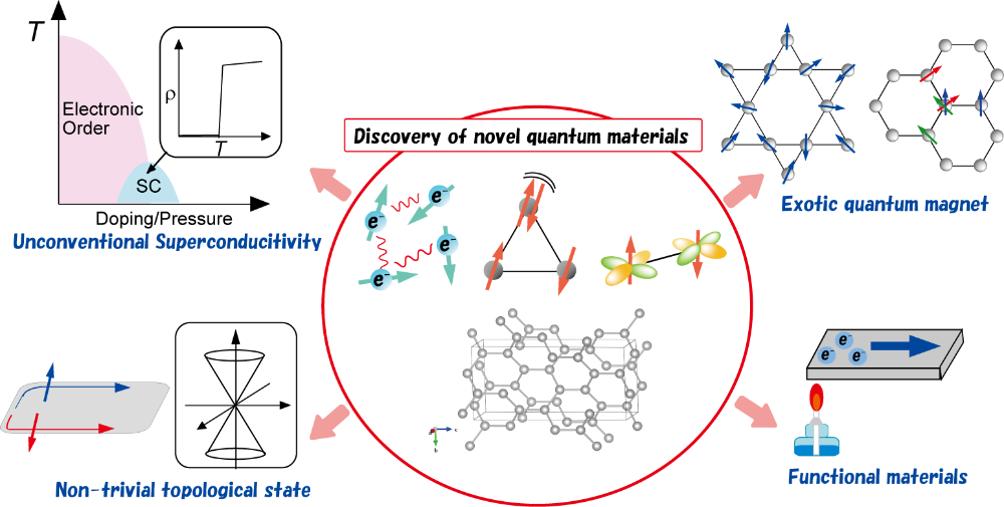
图 2. 几类量子材料及其一些潜在发展前景。图片来自德国马普所 Takayama 博士课题组。

如上这么八股空谈，估计读者已经不耐烦了。应对之道，就是举一个例子。这样的例子，既要扣住前沿，又要具有一定的普适性，要找到颇不容易。

此例来自量子计算和 (拓扑) 超导物理领域，其前沿和新颖性自然不是问题。该领域的目标之一，就是要实现用于高度容错量子计算的马约拉纳零能模 Majorana zero - mode(MZMs，泛指马约拉纳费米子)。在构建这些 MZMs 的物理方案中，最接近应用的方案是由常规 s 波超导与其它体系组成的异质结而来，例如：(1) 超导 - 拓扑绝缘体异质结，界面处有 MZMs；(2) 超导 - 半导体异质结 (包括半导体纳米线)，边缘态有 MZMs；(3) 超导 - 磁性原子链 / 纳米线异质结构，链端部有 MZMs；如此等等。本文只讨论第 (3) 类，即沉积于超导基底上的磁性原子链 hybrid 结构，其两端可能存在 MZMs，如图 3(A) 所示。

物理人很早就理论预言，一维磁性原子链两端存在 MZMs。诸如 Mn、Fe、Co 原子链,沉积于 Nb、Al 等常规超导基底上，即可实现这一目标，如图 3(B) 所示。这一方案之所以引起广泛关注，原因在于：(1) 对超导 - 磁性 hybrid 结构及其电子态，物理人早就烂熟于心，摩拳擦掌的心情自然可以理解；(2) 利用 STM 等技术，在超导表面对这些磁性原子进行操控，也是物理人驾轻就熟之术；(3) 运用 STM 对原子链中原子进行逐个扫描和诊断的技术，也逐渐成熟。这些条件，使得诸多物理人有些乐观，以为开展探索不会比易如反掌难多少。

事实是，这样的探索模式遇到了很大挑战。   (a) 理论处理此类一维磁性原子链问题，都是基于相当程度简化后的近似模型。例如，一些工作只考虑一维链结构、只考虑 Zeeman 能、只考虑超导序参量和对应的哈密顿。需要指出，考虑了这些物理元素后，简化模型的确也揭示出若干新的效应，复原出若干预期的结果。诸如原子链端的 MZM 态，很早就得到这些简化模型的预言，给人以水到渠成之感。

(b) 实验上制备出此类一维原子链，如图 3 所示，其结构和磁性的稳定性必定较低，结构畸变和缺陷在所难免。这些畸变和缺陷，使得原子链总伴有难以消弭的低能电子激发态，出现一些附加效应。例如，除了端部的 MZMs 外，原子链侧边也会出现的所谓“双眼”特征 (double eyefeature，可理解为一对一对的眼睛，如后图 4 所示)。这些激发态的存在，给实现和操控纯净的链端 MZM 态，带来很大不确定性。

   

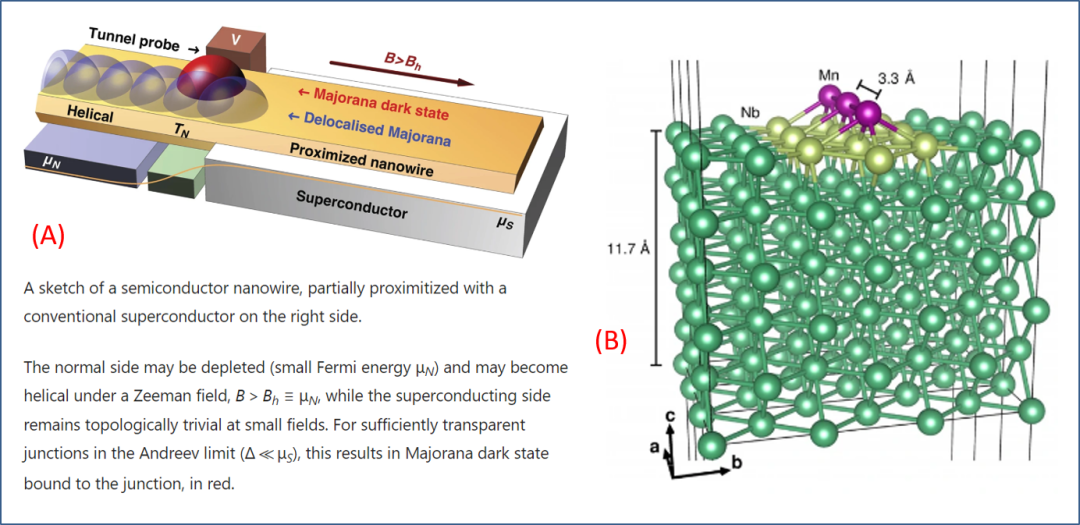
图 3. (A) 超导近邻效应，使得沉积于常规超导表面上的磁性或半导体纳米线 (proximized nanowires) 端部形成 MZMs，从而为 Majorana 和量子比特编织提供物理支撑。(B) 磁性 Mn 原子链生长于 Nb 超导表面的原子构型示意图。这样形成的磁性一维原子链 - 常规超导异质结不难制备。

遗憾的是，目前的理论模型，未能准确处理这些体系中存在的这些结构畸变和缺陷，未能很好地考虑原子链的准一维、局域二维 / 三维的结构特征。毕竟，完美的一维原子链只是一种理想化，各种原子结构和量子涨落不可避免。最致命的是，这些涨落或激发本身的能标，与 MZMs 的能标不相上下。其结果是，这些原子链侧边的电子结构涨落、磁性涨落及其与超导序参量的耦合，不能忽略，但理论上却未能得到很好处理。实验上，这些结构畸变和低能激发，使得测量的信号中混杂无序，要提取 MZM 零能模就变得困难。

那怎么办呢？既然这些困难的根源来自不能忽略的低能标过程，既然面对窘境时常用的前两种应对之法 (模型严格解和机器学习 GPT) 暂时无法发挥作用，那就不妨采取第三类“硬上强推”之法。

来自澳大利亚那所著名的墨尔本大学 (University of Melbourne) 的 Stephan Rachel 教授团队，与米国伊利诺伊大学芝加哥分校、日本冈山大学和德国汉堡大学的国际团队合作，似乎另辟它途，对这一问题展开了强攻。他们针对 Mn / Nb (110) 和 Fe / Nb (110) 两类体系，基于第一性原理计算，破纪录地考虑费米面上下近百支能带的贡献，构建了包含 80 个能带的 Bogoliubov - deGennes 超导有效模型。与此同时，对磁性原子链，模型则考虑了扩展到四个近邻原子的基本单元及单元内的载流子跃迁进程。这一“强推硬上弓”的作派，的确很好复现了简化模型给出的所有结果，包括 MZMs。除此之外，更为重要的是，他们的计算也清晰展示出原子链侧边的低能激发物理特征，包括那所谓的“双眼”效应，如图 4 所示。这些“清澈的双眸”，栩栩如生排列在那里，令人震撼！

不仅如此，这一团队竟然还亲自下场，对他们的计算预言开展实验验证。他们针对 Mn / Nb (110) 和 Fe / Nb (110) 两类体系的实验表征，很好地验证了理论计算结果，包括 MZMs 特征、“双眼”特征及其它侧边低能激发特征。一般而言，此类工作的理论计算结果已经足够强悍，值得发表。但 Rachel 教授他们显然有意犹未尽之感，亲自下场实验演示，令人可敬可佩！

   

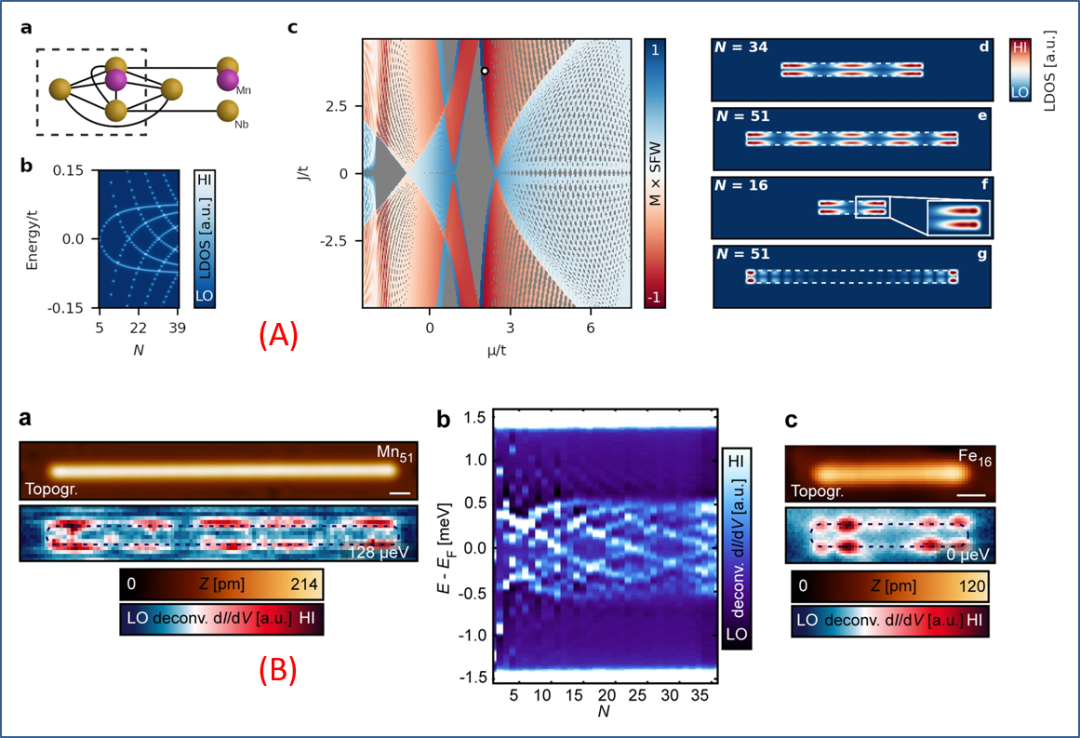
图 4. Stephan Rachel 教授团队展示的包括 80 个能带的模型计算结果 (A) 及实验测量结果 (B)。详细图题说明可参见论文，但横跨原子链两侧的一对一对 eyes (double eyes) 在理论计算和实验测量结果中清晰可见。

 





审核编辑：刘清