介绍支持向量机的基础概念

支持向量机（Support Vector Machine）是一种较知名的机器学习算法，该算法由俄罗斯数学家Vladimir Vapnik创立。  

下文介绍支持向量机的基础概念：线性可分的定义（二分类的线性可分定义）    

一、基于二维特征空间感性认识对线性可分  

（1）线性可分（Linear Separable）  

如果训练样本集的特征空间如图一所示，其中的圆圈和叉可被一条直线划分，则该训练样本集为线性可分。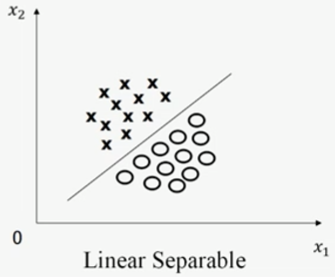  



图一，图片来源：中国慕课大学《机器学习概论》  

（2）线性不可分（Nonlinear Separable）  

如果训练样本集的特征空间如图二所示，其中的圆圈和叉不可被一条直线划分，则该训练样本集为线性不可分。

 

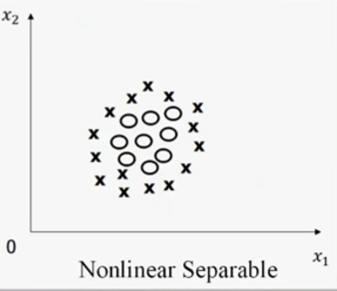
图二，图片来源：中国慕课大学《机器学习概论》    

二、线性可分的定义  

（1）二维特征空间下线性可分的定义   如图三所示，二维特征空间的两个维度分别为x1、x2，并假设该特征空间分布如图三的训练样本，训练样本包括圆圈和叉，圆圈采用类别标签C1表示，叉采用类别标签C2表示。

基于以上假设，图三特征空间中存在一条直线将训练样本分类为C1和C2，并假设该直线的方程为： ω1x1+ω2x2+b=0 其中，ω1和ω2分别为x1和x2的权重，b为偏置。

再规定：C1侧空间由ω1x1+ω2x2+b>0表示，C2侧空间由ω1x1+ω2x2+b<0表示（也可规定C1侧空间由ω1x1+ω2x2+b<0表示，C2侧空间由ω1x1+ω2x2+b>0表示）。  

 

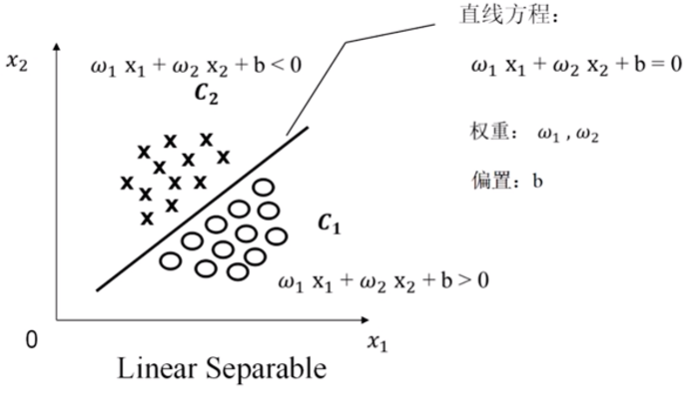
图三，图片来源：中国慕课大学《机器学习概论》  

再假设N个训练样本的标签为：{(X1,y1),(X2,y2),…,(XN,yN)}，其中Xi=[xi1，xi2]T（二维特征空间每个训练样本只包含xi1，xi2两个分量），yi={+1，-1}，当Xi的类别标签为C1时，yi的值为+1，当Xi的类别标签为C2时，yi的值为-1（该规定可方便定义。也可规定当Xi的类别标签为C1时，yi的值为-1，当Xi的类别标签为C2时，yi的值为+1，±1也可被替换为绝对值不同的数字）。  

基于以上假设和规定，二维特征空间的线性可分的定义如下： 一个训练样本集{(X1,y1),(X2,y2),…,(XN,yN)}，在i=1~N线性可分是指存在（ω1，ω2，b），使得对i=1~N，有： 1）若yi=+1，则ω1x1+ω2x2+b>0 2）若yi=-1，则ω1x1+ω2x2+b<0  

二维特征空间线性可分向量形式的定义如下： 假设Xi=[xi1，xi2]，ω=[ω1，ω2]T，那么： 若yi=+1，则ωTXi+b>0；若yi=-1，则ωTXi+b<0，即yi(ωTXi+b)>0。  

（2）n维特征空间线性可分的定义（含个人理解）  

根据二维特征空间线性可分向量形式的定义，可推广至n维特征空间线性可分向量形式的定义：即假设Xi=[xi1，xi2,…,xin]，ω=[ω1，ω2,…,ωn]T，那么一个n维训练样本集 {(Xi,yi)}在i=1~N线性可分是指存在ω和b，使得对 i=1~N，有yi(ωTXi+b)>0。        

审核编辑：刘清