

基于神经网络和无迹卡尔曼滤波融合的天线罩误差斜率估计方法
RF/无线
描述
虞卞雨萱 1,陆科林 1 ,符启恩 1,张宁 2
(1. 东南大学自动化学院,南京 210096; 2. 北京机电工程研究所,北京 100074)
【引用格式】虞卞雨萱,陆科林,符启恩,等。 基于神经网络和无迹卡尔曼滤波融合的天线罩误差斜率估计方法[J]。战术导弹技术,2023(1):121-131.
DOI:10.16358/j.issn.1009-1300.20220183
摘 要为消除导引头天线罩引入的瞄准误差对制导系统稳定性和精度造成的负面影响,提出了一种基于神经网络和无迹卡尔曼滤波融合的天线罩误差斜率估计方法。考虑先验模型知识,分别建立导引头、自动驾驶仪、弹目相对运动系统和弹体动力学系统的动态模型,选取真实视线角、视角和天线罩误差斜率作为状态变量,根据视线角观测值建立测量模型。考虑到模型的不确定性,基于神经网络技术学习非线性滤波模型中的动力学方程,结合无迹卡尔曼滤波技术,根据所学习的代理模型和带噪声的系统量测,对天线罩误差斜率等状态进行实时在线估计。与传统采用非线性滤波技术的天线罩误差斜率估计方法相比,本方法基于数据驱动思想,减少了对精确动力学模型的依赖,能有效消除模型不确定性的影响。与单纯采用离线训练构造的神经网络相比,本方法结合贝叶斯滤波理论,对实时数据具有更强的适应性。经多次仿真实验,证实该方法能够有效控制预测误差,具有较高精度。
1 引 言
现代战争中,出于人道主义和有效打击的考量,精准的点目标打击逐渐取代了大面积轰炸,如何实现精确制导成为各国学者关注的重点。雷达寻的导弹是精确制导武器的代表之一,它利用雷达导引头获得目标的角度观测,并结合制导律实现目标跟踪,进而精确打击,这个角度观测即为视线角(Line of Sight Angle,LOS)。 出于流线型的外形需求和防止气流扰动影响天线测量结果的考虑,雷达导引头并非直接暴露在导弹头部,而是罩有一个保护装置:导引头天线罩(Antenna Radome)[1]。但是天线罩会影响电磁波的传输[2],使电磁信号发生衰减、折射和反射等效应,从而造成瞄准线误差,形成天线罩误差角,这种测量误差将降低有效导航比,增大脱靶量[3]。更严重的是,这使得弹体姿态耦合到导引头,在制导回路内部形成一条寄生回路,严重影响制导系统的稳定性[4],加大了控制难度。
为避免天线罩误差带来的负面影响,最直接的思路是对天线罩进行精确建模,文献[5]根据电磁波折射理论推导了波束指向偏移模型,创新地结合了相控阵天线阵列测角原理,成功定位了有天线罩时检测角所对应的最大波束指向角度,提升了检测角误差的准确性,将误差从1°降低到0.1°以下。 另一种思路是获取天线罩误差斜率估计,从而对天线罩误差进行补偿。常见的估计方法有传统的非线性滤波估计、多模型算法和机器学习等。传统的非线性滤波是对经典的线性卡尔曼滤波(Kalman Filter,KF)的非线性变种,常见的有扩展卡尔曼滤波(Extended Kalman Filter,EKF)、无迹卡尔曼滤波(Unscented Kalman Filter,UKF)等。
文献[6]利用扩展卡尔曼滤波方法,结合弹目相对运动和导引头模型建立非线性滤波器,对天线罩斜率进行估计并用于补偿,显著改善了导弹的稳定性和制导精度。文献[7]则在此基础上进行了三维模型下的滤波设计:纵侧向通道联合估计视线角速率和天线罩误差斜率的扩展卡尔曼滤波器,进一步提高了天线罩误差影响下的制导精度。文献[8]提出了一种基于无迹卡尔曼滤波的隔离度在线补偿方法,首先建立了包含天线罩误差的雷达导引头隔离度模型,运用该补偿方法,在速度指向误差和目标常值机动输入下均能估计出天线罩误差斜率,从而改善了制导性能,提高了制导精度。
文献[9]基于扩展卡尔曼滤波的方法通过建立雷达导引头的寄生环模型,实现实时补偿,提升导弹的稳定性和制导精度,但是该方法也仅适用于能够精确建模的情况。 利用多模型算法估计天线罩斜率的思路最早是由Yueh在文献[10]中提出,其后有许多学者对该方法进行了进一步研究。例如,金鹏飞在文献[11]中采用模型参考自适应算法对天线罩误差斜率进行在线估计,并针对算法中的参数选择问题,提出了改进的参数自适应调节律,实现了对天线罩误差斜率准确且快速的估计。
利用机器学习技术估计天线罩误差,文献[12]利用历史数据训练神经网络,实现了离线补偿。文献[13]提出了一种基于机器学习和修正物理光学方法的天线罩雷达截面计算方法。利用多层感知器(Multilayer Perceptron, MLP)模型估计了天线随机系统的散射机理,用函数拟合估计FSS层的频率响应与入射角、偏振度和频率的关系,从而提高了天线罩表面电流计算的精度,但是该方法完全依赖于历史模式,缺乏对实时数据的适应性。 除此之外,考虑到传统非线性滤波对模型精确性的高要求和机器学习对训练集外、实际情况中不可预测噪声的适应性问题,近年来,传统滤波与机器学习相结合的估计方法也被广泛关注。文献[14]提出一种基于粒子滤波(Particle Filter, PF)与长短期记忆网络(Long Short Term Memory Network,LSTM)融合的在线预测方法。粒子滤波方法需要精确的状态模型,而精确的转移方程往往难以得到,文献[14]利用历史数据训练LSTM模型作为PF的状态转移方程,从而解决了PF的经验方程依赖问题,同时PF还能给出不确定性表达。研究结果表明,该方法模型更新简单有效,预测精度好。
学习数据构建神经网络模型并配合序贯滤波器进行估计,这一方法在很多其他学科中广泛应用,如文献[15]融合长短期记忆神经网络与卡尔曼滤波,提出了一种混合模型KF-LSTM,其结果优于LSTM模型和KF模型单独使用的结果;文献[16]中用多层前馈神经网络(Feedforward Neural Network,FNN)对测量建模,再通过卡尔曼滤波器进行估计,其结果更接近真实值;文献[17]提出一种基于高阶容积卡尔曼滤波(High Order Cubature Kalman Filter,HCKF)和神经网络的状态估计算法,利用前馈神经网络建立状态空间模型,然后采用HCKF对新状态进行更新,从而实现对状态值的精确估计。为了使状态方程更好地预测状态变量的走向,文献[18]利用循环神经网络(Recurrent Neural Network,RNN)学习历史数据,对状态进行建模,在此基础上,利用集合卡尔曼滤波(Ensemble Kalman Filtering)进行反演,得到的结果更为精确,实现声速剖面波动的追踪。
综上所述,只应用传统非线性滤波技术进行估计的方法(如文献[6-9]),可以根据系统观测适应实时情况,但其估计精度完全依赖于动力学模型的准确性,仅适用于能够精确建模的情况。而仅使用离线训练构造的神经网络的估计方法(如文献[12-13]),从历史数据中学习模式,缺乏对实时数据的适应性。故本文参考文献[14-18]的思想,综合传统非线性滤波技术和神经网络的优点,提出一种基于神经网络和无迹卡尔曼滤波的估计方法。 本文针对二维弹目相对运动模型中存在状态方程部分未知的情况,提出利用神经网络学习历史数据建立状态转移方程,再结合无迹卡尔曼滤波进行状态的实时更新,从而得到天线罩误差斜率估计,是一种融合机器学习和传统非线性滤波方法的天线罩误差斜率估计方法。
2 系统建模
导弹制导控制系统的建模主要包括导引头、比例导引、自动驾驶仪、弹体动力学环节和弹目相对运动五个部分。如图1所示,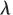 为真实视线角,
为真实视线角,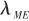 为视线角观测值,
为视线角观测值,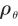 为天线罩误差斜率,
为天线罩误差斜率,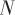 表示比例导引系数,
表示比例导引系数,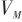 为导弹速度,
为导弹速度,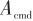 是制导律产生的控制指令,
是制导律产生的控制指令,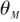 是弹体俯仰角。其中,
是弹体俯仰角。其中,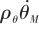 是视线角速度中的耦合分量。这个分量使得弹体姿态耦合到导引头中,在制导回路内部生成一条寄生回路。指令加速度
是视线角速度中的耦合分量。这个分量使得弹体姿态耦合到导引头中,在制导回路内部生成一条寄生回路。指令加速度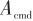 由理想的
由理想的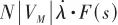 变为
变为
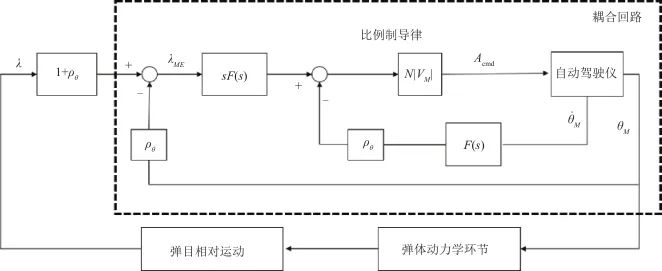
▲ 图1 制导控制系统▲ Fig.1 Guidance control system
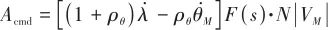 (1)
(1)
式(1)中,姿态角速度也参与到指令加速度的生成,形成了姿态角速率反馈回路。误差斜率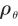 为负时,将导致姿态角速度正反馈,使姿态稳定回路发散;而当
为负时,将导致姿态角速度正反馈,使姿态稳定回路发散;而当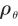 为正时,会降低导弹有效导航比,导致响应缓慢,造成较大的脱靶量。 综上所述,天线罩误差的存在破坏了原有的控制结构,严重影响了制导控制系统的稳定性和制导精度。
为正时,会降低导弹有效导航比,导致响应缓慢,造成较大的脱靶量。 综上所述,天线罩误差的存在破坏了原有的控制结构,严重影响了制导控制系统的稳定性和制导精度。
2.1 导引头
雷达波穿过天线罩会发生折射,此时根据导引头观测得到的视在目标位置不是真实的目标位置,如图2所示,在真实视线和虚假视线之间存在一个误差角,记作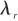 ,即天线罩误差角。
,即天线罩误差角。
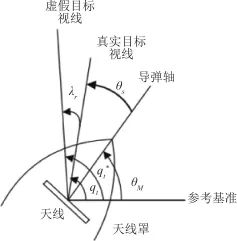
▲ 图2 带天线罩的导引头示意图▲ Fig.2 Seeker with radome 对于不同的视角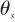 ,由于雷达波穿过天线罩罩壁位置的不同,折射情况不同,天线罩误差也就不同,天线罩误差
,由于雷达波穿过天线罩罩壁位置的不同,折射情况不同,天线罩误差也就不同,天线罩误差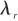 一般为视角
一般为视角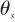 的函数。文献[19]中给出天线罩瞄准误差的经验公式:
的函数。文献[19]中给出天线罩瞄准误差的经验公式:
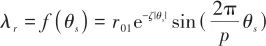 (2)
(2)
式中,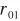 为天线罩瞄准误差的最大幅值,
为天线罩瞄准误差的最大幅值,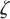 为一个正常数,
为一个正常数,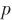 为周期。本文中取
为周期。本文中取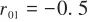 ,
,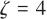 ,
,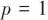 ,此时天线罩误差随视角变化曲线如图3所示。
,此时天线罩误差随视角变化曲线如图3所示。
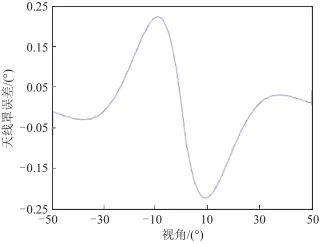
▲ 图3 天线罩误差随视角变化曲线▲ Fig.3 Radome error curve with angle of view 对式(2)求导,得到天线罩误差斜率的经验公式:
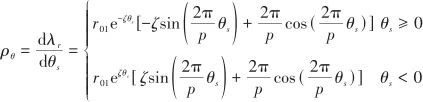 (3)
(3)
天线罩误差影响下二维弹目几何关系如图4所示,真实视线和参考方向的夹角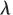 为真实弹目视线角,真实视线与虚假视线的夹角
为真实弹目视线角,真实视线与虚假视线的夹角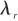 为天线罩误差角,弹体纵轴和参考方向的夹角
为天线罩误差角,弹体纵轴和参考方向的夹角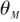 为弹体姿态角,弹体纵轴与导弹速度的夹角
为弹体姿态角,弹体纵轴与导弹速度的夹角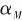 为导弹攻角,导弹速度与参考方向的夹角
为导弹攻角,导弹速度与参考方向的夹角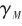 为航迹角,那么视角
为航迹角,那么视角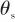 可以表示为
可以表示为
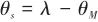 (4)
(4)
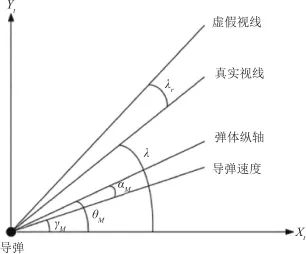
▲ 图4 天线罩误差影响下弹目几何关系▲ Fig.4 Geometric relations of projectiles affected by radome Errors 相应地,实际测量的弹目视线角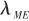 可以表示为
可以表示为
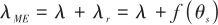 (5)
(5)
式(2)中,天线罩误差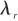 是视角
是视角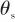 的非线性函数,对天线罩误差在视角为0处作泰勒展开,当视角
的非线性函数,对天线罩误差在视角为0处作泰勒展开,当视角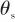 在较小范围内变化时,利用中值定理余项,实测弹目视线角
在较小范围内变化时,利用中值定理余项,实测弹目视线角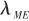 可进一步表示为
可进一步表示为
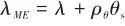 (6)
(6)
2.2 弹目相对运动
本文针对固定目标制导过程中的天线罩误差估计问题进行研究,假设目标静止,建立二维目标接近运动关系。如图5所示,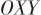 为弹体坐标系,
为弹体坐标系,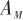 ,
,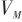 分别为导弹机动加速度和导弹速度,导弹速度与参考方向的夹角
分别为导弹机动加速度和导弹速度,导弹速度与参考方向的夹角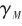 为航迹角,
为航迹角,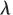 为真实弹目视线角,R为弹目距离。
为真实弹目视线角,R为弹目距离。
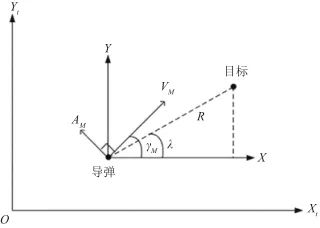
▲ 图5 弹目相对运动示意图▲ Fig.5 Projectile relative motion 假设目标的速度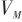 是常数,导弹和目标之间的相对运动建模如式(7)和式(8),相应的Simulink仿真模型如图6所示。
是常数,导弹和目标之间的相对运动建模如式(7)和式(8),相应的Simulink仿真模型如图6所示。
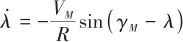 (7)
(7)
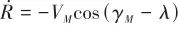 (8)
(8)
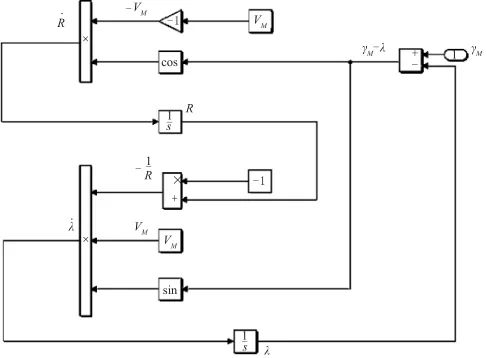
▲ 图6 弹目相对运动仿真模型▲ Fig.6 Simulation model of projectile relative motion
2.3 导引控制
比例导引律( 是应用最为广泛的导引方法之一,其基本思想是使导弹速度向量的转动角速度正比于目标视线的转动角速度,它能使导弹在目标机动时也能很好地实施攻击。 根据PNG制导律,利用量测得到的弹目视线角
是应用最为广泛的导引方法之一,其基本思想是使导弹速度向量的转动角速度正比于目标视线的转动角速度,它能使导弹在目标机动时也能很好地实施攻击。 根据PNG制导律,利用量测得到的弹目视线角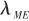 得到控制指令
得到控制指令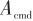 :
:
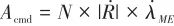 (9)
(9)
式中,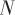 表示比例导引系数,
表示比例导引系数,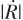 为弹目接近速度,根据式(6),可以推算得到视线角速度
为弹目接近速度,根据式(6),可以推算得到视线角速度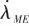 :
:
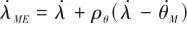 (10)
(10)
代入式(7)得
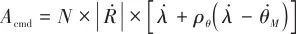 (11)
(11)
2.4 自动驾驶仪
假设自动驾驶仪为一阶延时环节,时间常数为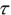 ,则环节传递函数为
,则环节传递函数为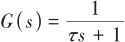 。输入为制导控制模块输出的制导指令
。输入为制导控制模块输出的制导指令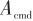 ,输出为实际控制指令
,输出为实际控制指令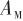 。
。
2.5 弹体动力学模型
弹体动力学模型即机动控制对弹体运动学物理量的作用方程。这里推导从控制指令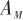 到导弹姿态角(俯仰角)速率
到导弹姿态角(俯仰角)速率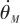 的传递函数。 首先,机动加速度
的传递函数。 首先,机动加速度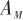 正交于导弹速度
正交于导弹速度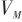 ,可得航迹角速率
,可得航迹角速率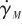 :
:
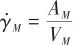 (12)
(12)
弹体姿态角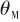 是弹体纵轴和参考方向的夹角,由图4可知,可以表示为
是弹体纵轴和参考方向的夹角,由图4可知,可以表示为
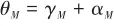 (13)
(13)
导弹机动性参数中的转弯率时间常数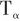 的定义如下:
的定义如下:
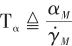 (14)
(14)
代入(13)得
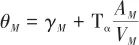 (15)
(15)
对式(15)求导得到姿态角速率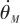 :
:
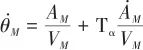 (16)
(16)
对式(16)进行拉普拉斯变换最终得到弹体动力学模型:
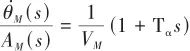 (17)
(17)
2.6 完整的系统建模
考虑比例导引的带误差雷达寻的制导系统建模如图7所示,包括视线角量测、导引控制、自动驾驶仪模块和弹目相对运动、机体动力学等模块,至此仿真模型建立完毕。
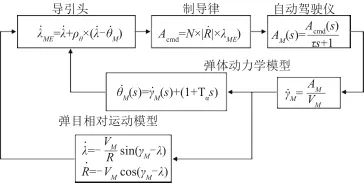
▲ 图7 考虑比例导引的带误差雷达寻的制导系统▲ Fig.7 Radar homing guidance system with error considering proportional guidance 将导弹速度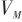 和比例导引系数
和比例导引系数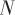 设为常数,取真实视线角
设为常数,取真实视线角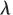 、视角
、视角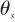 和天线罩误差斜率
和天线罩误差斜率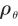 作为3个状态变量,以视线角观测值
作为3个状态变量,以视线角观测值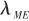 为观测量,分别建立系统的状态模型和观测模型。本节先根据几何关系建立观测模型,随后将利用神经网络建立状态转移模型。 令
为观测量,分别建立系统的状态模型和观测模型。本节先根据几何关系建立观测模型,随后将利用神经网络建立状态转移模型。 令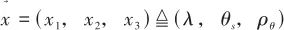 ,根据式(4)和式(6),观测方程可写成:
,根据式(4)和式(6),观测方程可写成:
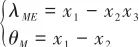 (18)
(18)
3 基于神经网络和无迹卡尔曼滤波融合的天线罩误差斜率估计方法
3.1 神经网络预测
神经网络,也称为人工神经网络 (Artificial Neural Networks,ANN),是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。其模型结构大体可以分为前馈型网络和反馈型网络(也称为Hopfield网络)两大类。本文采用多层前馈神经网络拟合状态预测方程。 前馈神经网络[20](Feedforward Neural Network,FNN),简称前馈网络,是一种最简单的神经网络,在各行各业中应用广泛。 前馈神经网络采用一种单向多层结构,其中每一层包含若干个神经元,各神经元可以接收前一层神经元的信号,并产生输出到下一层。其中,第0层为输入层,最后一层为输出层,其他中间层叫做隐藏层(或隐含层),隐藏层可以是一层,也可以是多层。 前馈神经网络中无反馈,信号从输入层向输出层单向传播。一个典型的多层前馈神经网络如图8所示,该神经网络模型共有4层,分别为输入层、2层隐藏层和输出层,各个层之间通过权系数进行连接,输入输出层在两端,中间隐藏层的节点数根据实际情况进行选取。
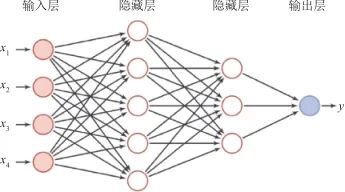
▲ 图8 前馈神经网络▲ Fig.8 Feedforward neural network 与传统的解析建模相比,神经网络模型可以更好地利用数据,直接学习到映射关系,而不需要进行复杂的分析和推导,避免了人工推导可能出现的错误。另外,对于模型过于复杂或者模式未知的系统,神经网络也可以进行拟合。 因此,本文使用基于前馈神经网络的状态预测网络模型,输入为一段时间内状态序列,输出为整体后移一个时刻的状态序列。 网络模型结构如图9所示,网络主体由2层节点数为16的Dense层构成,输出层为节点数为3的全连接层。网络训练指标为均方误差(最小),优化器为Adam优化器。
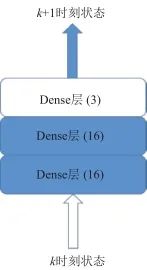
▲ 图9 网络模型▲ Fig.9 Network framework
3.2 无迹卡尔曼滤波
无迹卡尔曼滤波的核心是无迹变换(Unscented Transform,UT),其主要思想是先产生一组一、二阶矩与状态变量的信息相同的Sigma点,然后对每个Sigma点进行非线性函数变换,最后用变换后的Sigma点集来确定输出值的矩。UKF算法的预测步计算均是非线性的,可以避免线性化过程中产生的误差,提高估算的准确性。 UKF的具体流程为 (1)初始化状态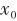 的初始均值
的初始均值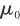 和协方差
和协方差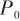 。 (2)计算对应的Sigma点集:
。 (2)计算对应的Sigma点集:
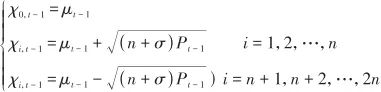 (19)
(19)
式中,n为状态变量个数,这里为3;σ为一个与n有关的系数。 (3)计算加权系数:
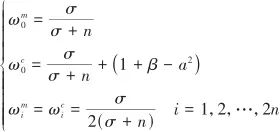 (20)
(20)
(4)预测步:
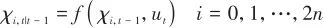 (21)
(21)
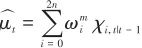 (22)
(22)
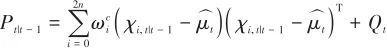 (23)
(23)
式中,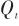 是过程噪声协方差。 (5)观测:
是过程噪声协方差。 (5)观测:
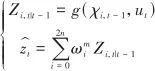 (24)
(24)
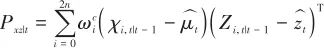 (25)
(25)
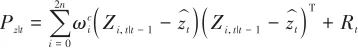 (26)
(26)
式中,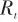 为测量噪声协方差。 (6)卡尔曼增益:
为测量噪声协方差。 (6)卡尔曼增益:
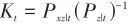 (27)
(27)
(7)更新结果:
 (28)
(28)
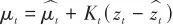 (29)
(29)
3.3 基于神经网络和无迹卡尔曼滤波融合的估计方法
在本文研究的天线罩模型中,存在状态方程部分未知的情况,这里利用神经网络基于历史数据学习到完整状态方程,再应用无迹卡尔曼滤波,结合实时观测得到状态估计。该估计方法的流程示意图如图10所示,用预先训练好权重的前馈神经网络作为无迹卡尔曼滤波的预测方程f。
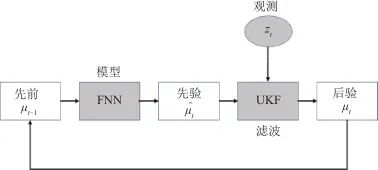
▲ 图10 基于神经网络和无迹卡尔曼滤波融合的估计方法流程▲ Fig.10 Method based on neural network and unscented Kalman filter UT变换得到Sigma点集后,计算预测步如下:
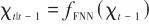 (30)
(30)
结合加权系数得到预测步的均值和方差。随后的观测更新步与3.2节相关内容相同,用导引头观测值更新状态估计,从而得到t时刻最终的估计结果:
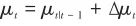 (31)
(31)
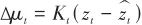 (32)
(32)
然后利用这个估计结果进行下一时刻的状态预测,迭代计算得到完整的状态估计序列。
4 仿真结果及分析
因为本文解决的实际问题存在状态方程部分未知的情况,只使用传统非线性滤波技术无法完成估计,这里仅与完全依赖历史数据的神经网络估计方法设计对比实验。 考虑到卡尔曼滤波及其变种都是基于马尔可夫模型,且兼顾实际模型本身的时序特性,仅利用神经网络技术和本文提出的估计方法都采用时序的输入输出进行网络训练。
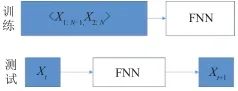
▲ 图11 神经网络序列训练与测试示意▲ Fig.11 Training and testing of FNN 具体地,仅用神经网络的估计方法的训练集输入为当前观测,输出为状态变量。而本文方法采用的训练集,以输入为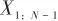 、输出为
、输出为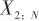 为例,时间上向后预测一步。 本文取序列长度为2生成训练集训练模型,然后用较长的完整序列进行测试。 设计64组状态初值正态分布的训练集,状态初值如表1所示。
为例,时间上向后预测一步。 本文取序列长度为2生成训练集训练模型,然后用较长的完整序列进行测试。 设计64组状态初值正态分布的训练集,状态初值如表1所示。
▼ 表1 训练集初值设定▼ Table 1 Initial value of training set

设采样时间为0.1 s,运行30 s,生成长度为300的序列,分别将上述长序列分割为298个长度为2的短序列,并打乱小序列间顺序。按不同初值情况,重复以上步骤64次,并再次打乱,生成包含19072条短序列的数据集。设验证集比例为10%,测试集比例为10%,最终随机取1908条序列为验证集,1907条序列为测试集,剩余80%的15257条短序列为训练集。对训练数据的各维度分别进行最大最小值归一化,即:
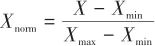 (33)
(33)
测试序列的初值如表2所示,长度为300。
▼ 表2 测试序列初值设定▼ Table 2 Initial value of test sequence

仅用神经网络估计的状态曲线如图12所示,其中,图12(a)为状态的估计值和实际值对比,粗实线表示神经网络方法估计所得,细实线表示实际状态,可见估计的状态与实际状态偏差较大;图12(b)为3个状态估计值和实际值的误差曲线。
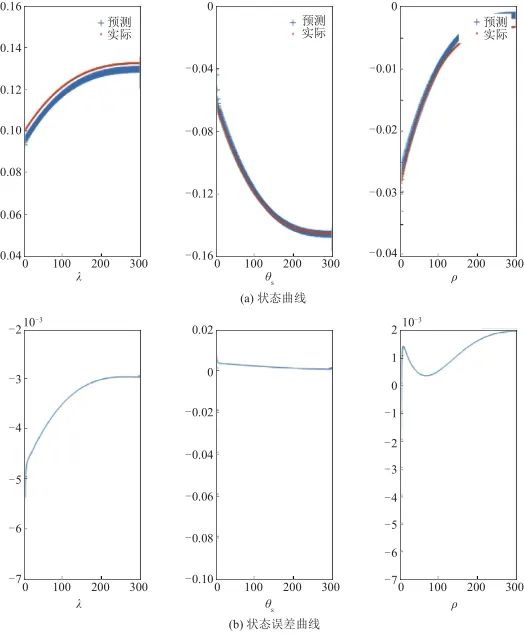
▲ 图12 仅用神经网络的状态测试结果▲ Fig.12 State testing results of neural network 经神经网络和无迹卡尔曼滤波融合的估计方法得到的状态曲线如图13所示,其中,图13(a)为状态的估计值和实际值对比,粗线表示本文方法估计所得,细线表示实际状态,可见估计的状态与实际状态较为接近;图13(b)为3个状态估计值和实际值的误差曲线。
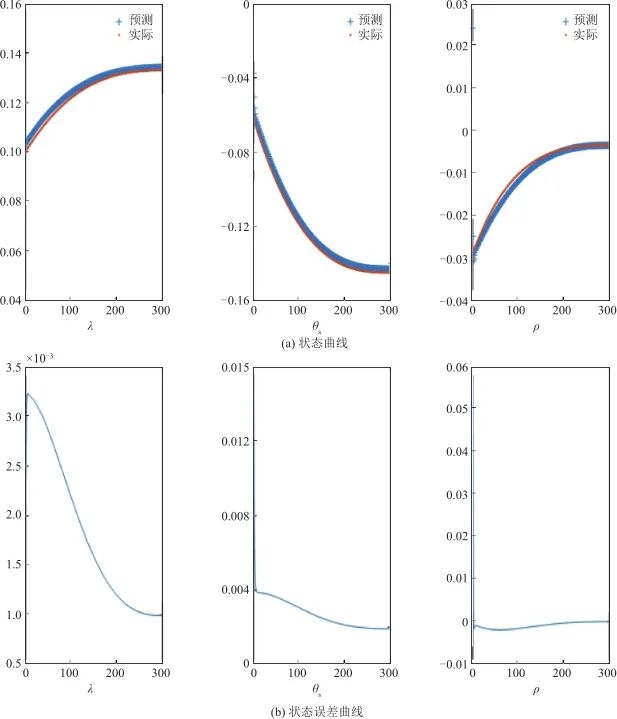
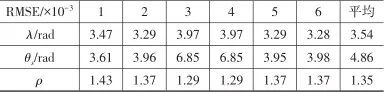
▲ 图13 本文方法状态测试结果▲ Fig.13 State testing results of the method 对比可见,本文提出的结合使用传统非线性滤波技术和神经网络的方法,估计准确度更高。 分别取多组随机初值重复实验,仅采用神经网络的估计方法和本文方法的估计误差(这里用均方根误差RMSE表示)分别如表3和表4所示,其中单纯采用神经网络的方法得到的天线罩误差斜率估计平均RMSE为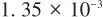 ,本文天线罩误差斜率估计的平均RMSE更低,为
,本文天线罩误差斜率估计的平均RMSE更低,为 。
。
▼ 表3 神经网络实验结果▼ Table 3 Experimental results of the neural network
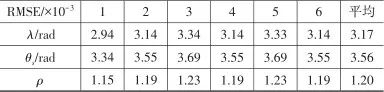
▼ 表4 本文方法实验结果▼ Table 4 Experimental results of the method
5 结 论
针对导引头天线罩误差问题,本文首先介绍了该误差对制导系统的稳定性和精度造成的负面影响,然后以估计天线罩误差斜率为目标,提出了一种融合神经网络和无迹卡尔曼滤波的天线罩误差斜率估计方法。分别以真实视线角、视角和天线罩误差斜率为状态变量,视线角为观测变量,建立非线性滤波模型,其中,预测函数用预先训练完成的多层前馈神经网络代替,迭代过程中利用观测实时更新状态,从而获得精度较高的状态估计。本方法无参数选择需求,易于工程实现,且对现实数据具有更好的适应性。经多次仿真实验,证实该方法能够有效控制预测误差,具有较高精度。
编辑:黄飞
-
卡尔曼滤波器介绍2008-07-14 0
-
自适应平方根无迹卡尔曼滤波算法2010-04-24 0
-
Matlab基于卡尔曼滤波的神经网络的程序2011-02-28 0
-
卡尔曼滤波器算法(C语言)2011-10-24 0
-
有谁做的是关于无迹卡尔曼滤波板块的,想请教一下问题2016-03-14 0
-
什么是电大尺寸天线罩与波导裂缝阵一体化仿真?2019-08-26 0
-
基于卡尔曼滤波器和多传感状态的融合估计算法是什么?2020-04-06 0
-
基于无迹卡尔曼滤波的四旋翼无人飞行器姿态估计算法_朱岩2020-06-04 0
-
卡尔曼滤波器是什么2021-11-16 0
-
基于霍夫-无迹卡尔曼滤波的目标检测与跟踪2013-08-19 807
-
基于自适应无迹卡尔曼算法的工业物联网数据融合处理2017-01-13 1140
-
结合神经网络的无迹卡尔曼滤波算法2017-12-08 1240
-
几种最优估计和卡尔曼滤波原理的学习课件免费下载2020-05-09 847
-
卡尔曼滤波(KF)与扩展卡尔曼(EKF)2023-05-10 488
-
卡尔曼滤波家族2024-01-14 898
全部0条评论

快来发表一下你的评论吧 !

