

支持向量机(核函数的定义)
电子说
描述
根据机器学习相关介绍(10)——支持向量机(低维到高维的映射),支持向量机可通过引入φ(x)函数,将低维线性不可分问题转换为高维线性可分问题。转换后支持向量机的优化问题可改写为:
最小化:1/2||ω||2+C∑δi或1/2||ω||2+C∑δi2,
限制条件:(1)δi≥0,i=1~N;(2)yi(ωTφ(Xi)+b)≥1-δi,i=1~N。
欲求解上述优化问题,需先知道φ(x)的形式。
但支持向量机的创始人Vladimir Vapnik提出结论:完成测试样本的类别预测不必须知道φ(x)的具体形式,如果对任意两个向量X1、X2已知:
K(X1,X2)=φ(X1)Tφ(X2)
则仍可以完成测试样本的类别预测(具体如何完成在下篇文章中叙述)。
上式中K(X1,X2)被定义为核函数(Kernel Function),核函数是一个实数(上式中φ(X1)Tφ(X2)为两个维度相同的行向量和列向量相乘的形式,其结果为一个实数)。
上述结论成立的一个必要条件是核函数K与低维到高维映射φ(x)具有一一对应的关系,即只有核函数K与映射φ(x)一一对应关系,核函数K才能代替φ(x)完成测试样本的类别预测。
一般情况下,核函数K与映射φ(x)具有一一对应关系,下文以两个案例说明核函数K与映射φ(x)的一一对应关系。
案例一:
假设:φ(x)是一个将二维向量映射为三维向量的映射,其中,二维向量X=[x1,x2]T,映射φ(x)=φ([x1,x2]T)=[x12,x1x2,x22];
再假设:X1=[x11,x12]T,X2=[x21,x22]T;
则φ(X1)=[x112,x11x12,x122],φ(X2)=[x212,x21x22,x222];
若核函数K(X1,X2)=φ(X1)Tφ(X2),则K(X1,X2)=[x112,x11x12,x122][x212,x21x22,x222]T=x112x212+x11x12x21x22+x122x222。
案例二:
假设:K(X1,X2)
=(x11x21+x12x22+1)2
=x112x212+x122x222+2x11x12x21x22+2x11x21+2x12x22
=φ(X1)Tφ(X2);
再假设:X=[x1,x2]T;
则φ(x)=φ([x1,x2]T)=[x12,x22,1,√2x1x2,√2x1,√2x2]T(该式中√代表根号,该式推导过程暂不知,若将X1=[x11,x12]T,X2=[x21,x22]T代入该式,再通过φ(X1)Tφ(X2)=K(X1,X2),可反推导出案例二中的核函数),φ(x)中各维度值可相互交换顺序。
但当核函数不能转化为两个φ(x)内积形式时,核函数与映射φ(x)不具有一一对应关系。因此,核函数需可以转化为两个φ(x)内积形式。
K(X1,X2)可转化为φ(X1)Tφ(X2)(即可转化为两个φ(x)内积形式)的充要条件:
(1)K(X1,X2)=K(X2,X1)(即核函数具有交换性)
(2)对于任意的Ci(i=1~N)和任意的N,有:
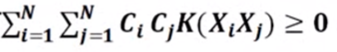
即核函数K具有半正定性。
审核编辑:刘清
-
#硬声创作季 人工智能入门课程:11. [2.6.1]--支持向量机(核函数的定义)Mr_haohao 2022-09-21
-
11. 2 6 支持向量机(核函数的定义) #硬声创作季充八万 2023-07-07
-
介绍支持向量机与决策树集成等模型的应用2021-09-01 0
-
基于支持向量机的预测函数控制2009-03-17 641
-
改进的支持向量机特征选择算法2009-04-03 430
-
基于改进支持向量机的货币识别研究2009-12-14 418
-
基于GMM超向量核函数的说话人识别2009-12-19 829
-
基于支持向量机的手势识别研究2010-01-22 651
-
双目标函数支持向量机在情感分析中的应用2017-01-03 702
-
组合核函数多支持向量机的直线电机建模2017-01-07 699
-
大数据中边界向量调节熵函数支持向量机研究2017-01-07 763
-
基于标准支持向量机的阵列波束优化及实现2017-11-10 793
-
模糊支持向量机的改进方法2017-11-29 719
-
基于支持向量机的测深激光信号处理2017-12-21 828
-
多核学习支持向量机应用音乐流派自动分类2018-01-09 1241
全部0条评论

快来发表一下你的评论吧 !

