如何对挑选出的demonstration示例进行排序

1 简介‍‍‍‍‍‍‍‍‍

    在demonstration selection的方法中，其中有部分方法也考虑到demonstration内部示例之间的顺序，虽然有的论文里提及他们的ICL方法对于demonstration内部示例顺序不敏感，但这些实验中考虑到的排列顺序还是不够全面，从而导致某些结论比较片面。毋庸置疑，如何对挑选出的demonstration示例进行排序是demonstration organization的重要部分。对于同样样本组成的demonstration，好的样本顺序可以让LLM有接近于SOTA的性能，而糟糕的样本顺序会让LLM的表现接近于随机猜测。就跟打牌一样，再好的手牌，不合理安排规划出牌顺序，很容易就会一败涂地。

2 Demonstration ordering

    为了更好的研究demonstration样本排列的影响，需要考虑在不同模型规模，样本数量以及不同模型上的表现。研究发现，随着模型规模的增加，demonstration不同样本排列的效果的方差有所缩小，但是依旧差距明显，即demonstration好的排列跟坏的排列之间的效果距离很大（见Subj数据集）。增加样本数量，依旧不能显著降低这其中的方差。另外，在A模型上表现良好的demonstration排列，在其他的模型效果往往不能得到保证，也就是好的demonstration排列并不能迁移到更多模型中去。

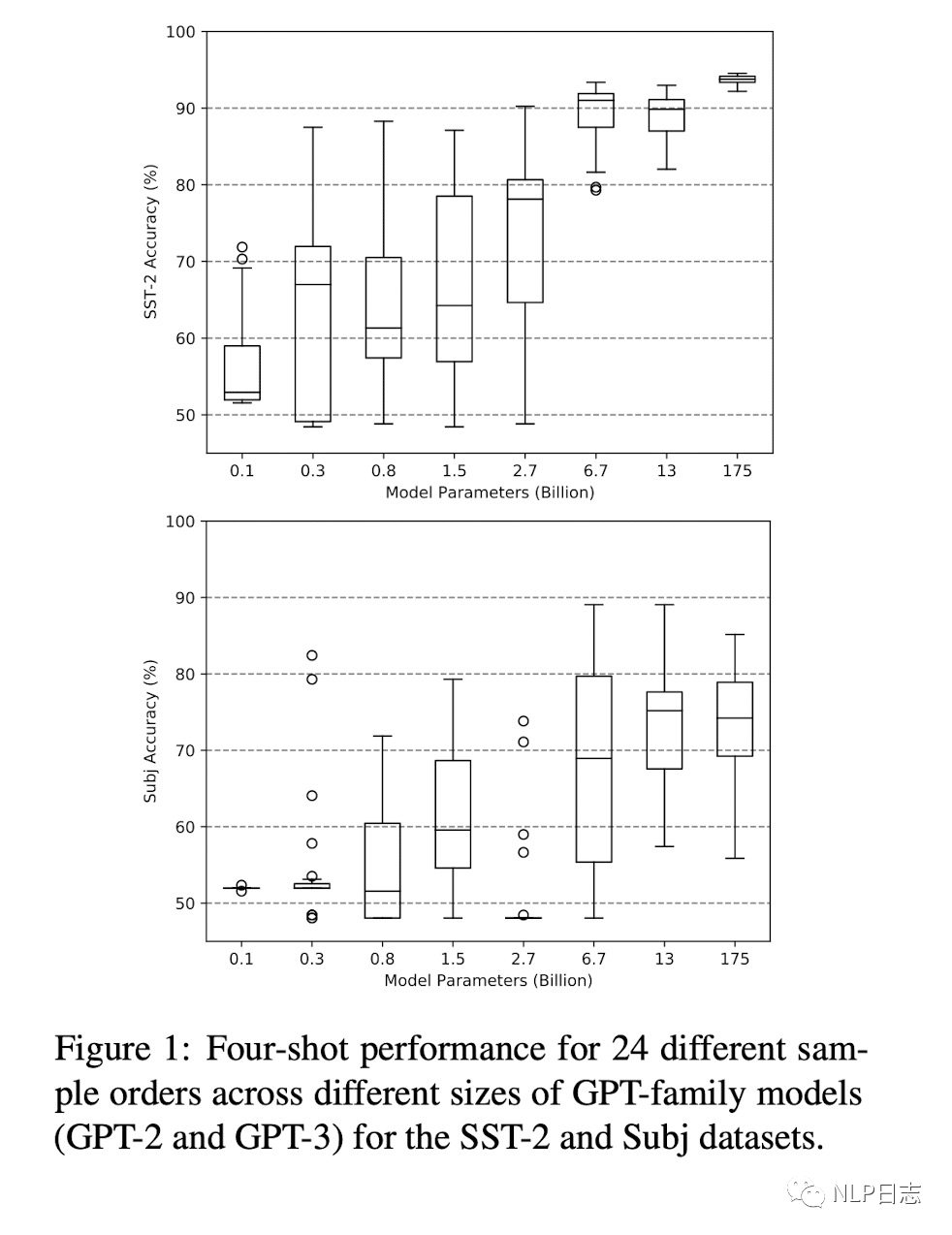
图1: 不同模型尺寸下demonstration ordering的影响

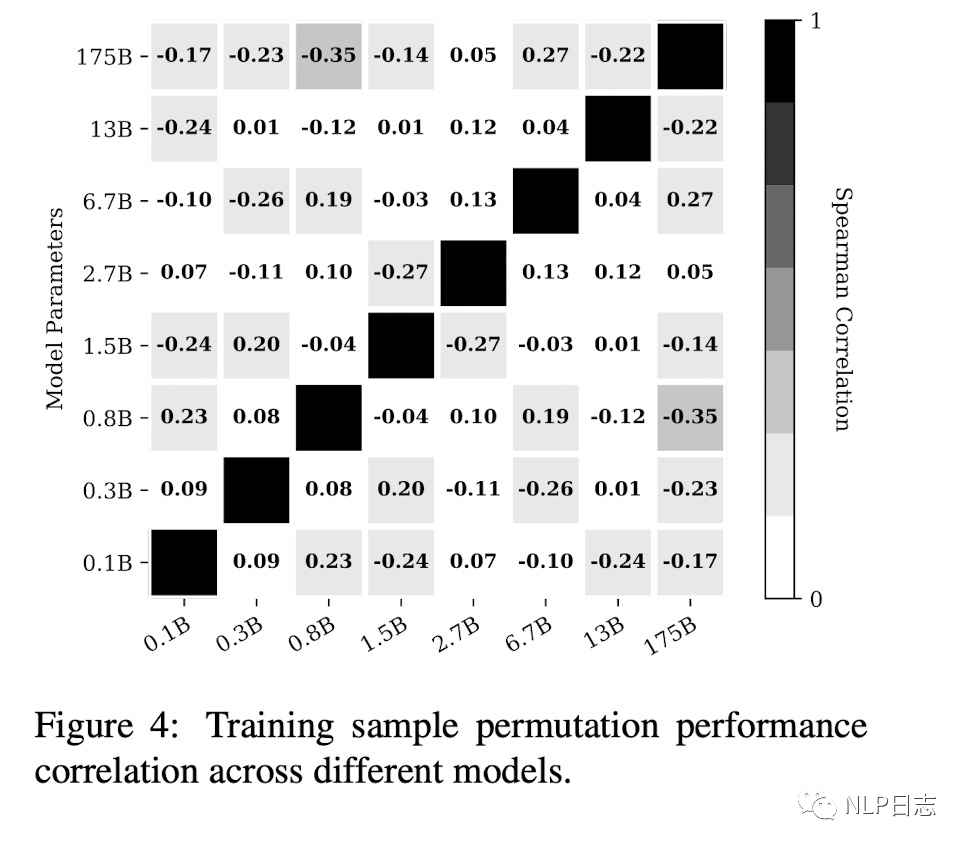
图2: demonstration ordering在不同模型见的迁移能力

    关于demonstration的排列，最简单的方式就是按照跟当前问题x的关系来排序。由于in-context learning中模型的输入都是demonstration+x(当前问题)，在demonstration中越靠后的示例距离当前的问题x的距离就越近，于是可以通过示例跟当前问题x的相似程度来对示例进行排序，跟当前问题x越相似的示例就放在demonstration越靠后的位置。

    目前确实存在若干种demonstration ordering的方法，但是最大的问题是在缺乏监督验证集的情况下自动选择更优的demonstration排列。于是就有研究提出自动构建探测集（probing set），具体流程如下     a) 给定一个训练集S={xi, yi}，i=1…n,利用一个模版转换函数（将样本数据转换成某种自然语言）获得一个自然语言数据集S’={ti}, ti=input:xi,type:yi。     b) 定义n个训练样本的所有排列函数（也就是demonstration的所有排列），F={fm},cm=fm(S’)，m=1,…,n!。每个cm都是n个t组成的一种排列。     c) 对于每一个候选排列cm，利用语言模型生成后续的序列，生成新的样本，对生成结果解析后得到模型生成测试集D。

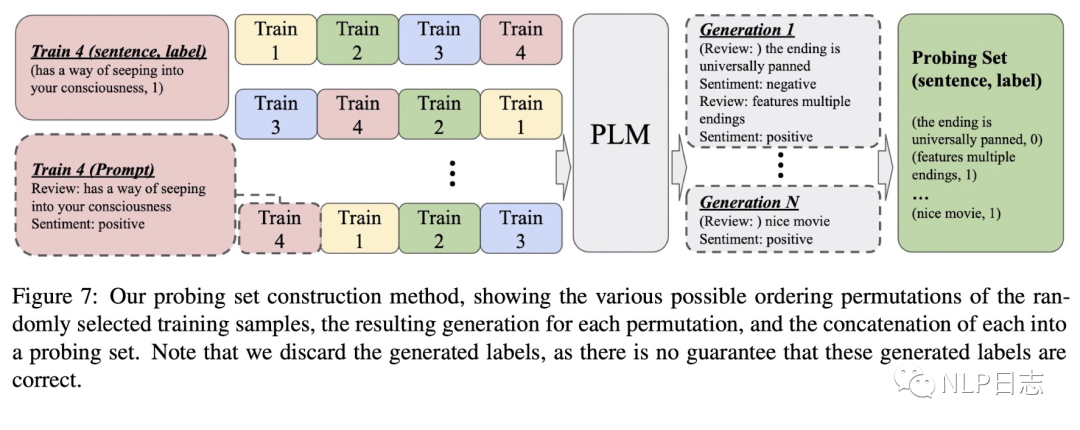
图3: probing set构造流程

    有了模型生成数据集后，研究者就提出了两种用于选择最佳demonstration排列的方法Global entropy(GlobalE)以及Local entropy(LocalE)。对于每个demonstration排列cm，在给定demonstration排列cm跟当前问题x的条件下，会预测所有标签y的概率，将概率最大的标签作为当前问题x的预测结果，从而计算整个探测集中所有预测标签分布的交叉熵作为排列cm的GlobalE得分。而LocalE得分则是计算每个探测集数据的预测交叉熵的平均值。简单的理解就是，如果在探测集上预测的标签分布相对平衡，那么对应的得分就比较高，作者就认为是比较好的demonstration排列。

    通过这两种方式选择的demonstration排列，效果上得到明显提升，并且这种方法还是比较鲁棒的，加入更多不好的demonstration排列只会让效果越来越差。

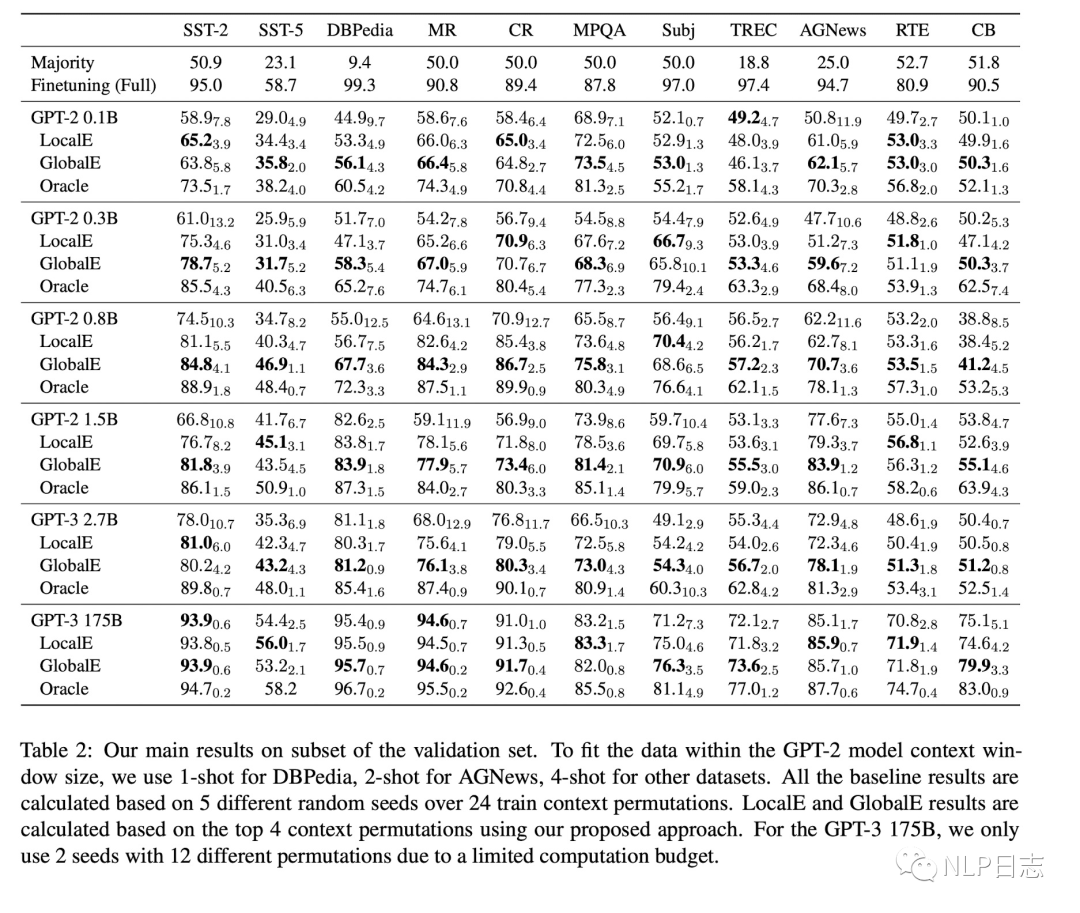
图4: 不同demonstration策略的效果对比

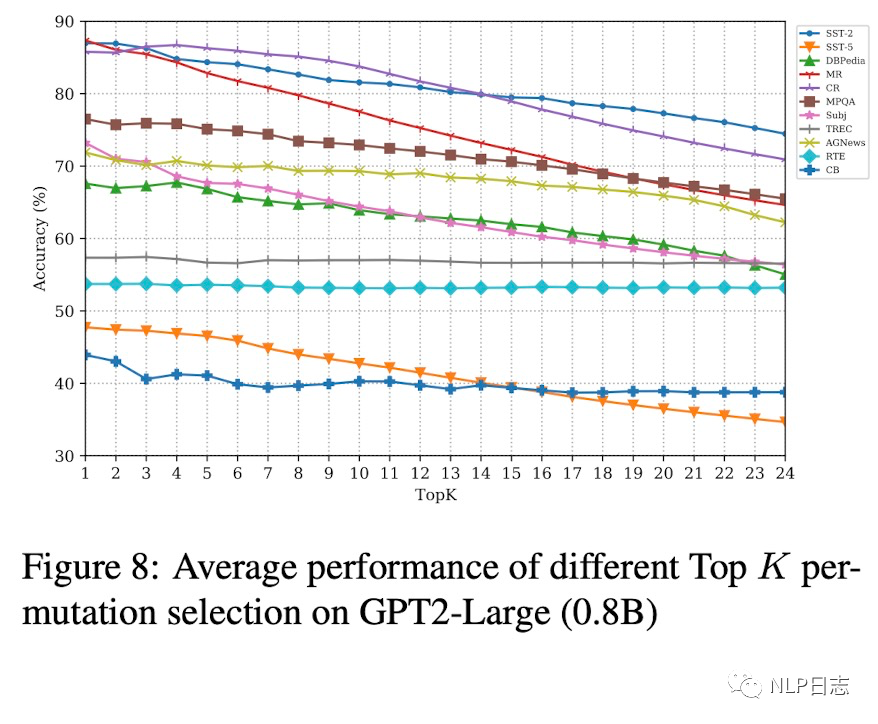
图5: 基于demonstration ordering选择的demonstration排列的的平均效果

3 总结‍‍‍‍‍‍‍‍

    Demonstration ordering目前看来还是一个值得进一步研究的问题，即便模型规模达到一定程度，依旧对此敏感。考虑到demonstration排列的数量跟训练样本库之间是一个指数关系，而目前看到绝大多数Demonstration ordering都是针对每个排列进行的，即便可以自动构建探测集，计算成本还是比较高的，很难考虑所有demonstration排列，目前除了根据与当前问题的相似度进行排序以及上一篇文章提到的马尔可夫决策过程可以处理，其他的方法都只停留在理论层面，很难在实际中大范围使用。