

戴维·M. 布雷苏:对微积分的思考
描述
积分讲授为累积
非常不幸的是, 对许多学生来说, 积分仅仅限于求面积、体积以及记忆求原函数的种种法则. 许多理由表明, 若不将积分理解为累积, 那么积分教学就是失败的. 我们指出其中三个理由。
首先, 历史告诉我们, 累积是一个直观的过程. 我们粗看一下历史. 古埃及人在发现四棱台的体积公式时几乎肯定应用了某种形式的累加增量. 中国人在公元 5 世纪以前就掌握了求体积的卡瓦列里方法.这是微积分很明显地跨越了文化的一个方面。
其次, 学生必定能掌握可以计算定积分或求出不定积分的软件. 虽然许多积分技巧对它们所提供的结构方面的洞察力来说是重要的, 但只有极少数人需要在课堂以外求原函数. 更有用的是将一个累积问题转化为定积分的能力。
最后, 学生若不能将积分理解为累积, 可能就不会认识到积分在求面积与体积以外的丰富应用. 积分是用来研究具有随时变换的累积量的事物的工具: 走过的距离、完成的工作、赚取的利润、生成的物资、环境恶化或改良的追踪, 等等。
我们甚至可以通过累积来介绍积分从而开始微积分教学. 这是美国亚利桑那州的汤普森 (Thompson) 所采用的方法.他的课程基于对下述本质的洞察: 微积分是研究变化的量之间的函数关系. 一个累积必定是一个函数, 描述在每个自变量值处累积了多少. 定积分首次出现时, 必定作为一个代表上限的变量的函数。
俄克拉荷马州的厄尔特曼开发了让学生通过累积进入积分的一系列练习, 让学生有机会构造对所涉及的原理的理解。
他给学生展示了美国航空航天局的一个月球车, 配上一枚电池可以工作 3 小时, 而且它在
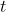
时刻的速率为
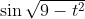
英里/时 (图 6.1). 学生在探究它最多离开机舱多远并仍可在那个时刻掉头时, 就学到了估计在小时间段上的距离. 正如从图像上容易看出的, 速率在前
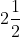
小时还多一点儿都是递增的. 更确切地说, 它在
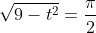
时取得最大值, 此时
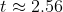
小时. 学生们会迅速领会到, 当速率递增时, 通过取初始时刻的速率与结束时刻的速率, 即可得到所走路程的一个上下界估计. 用一个简单的电子表格程序就足以得到合理的近似. 学生会认识到, 可以选取更短的时间区间以得到更精细的上下界, 从而得到更好的近似. 在此过程中, 可以向他们介绍求和记号, 这对他们所做的事情来说是很方便的. 此时可以向学生展示, 以行走时间为上限变量的积分是一种计量了实际累积的函数. 由于他们在第一次遇到定积分时, 定积分就以累积函数的形式出现, 因此这样一个函数对他们来说印象深刻。
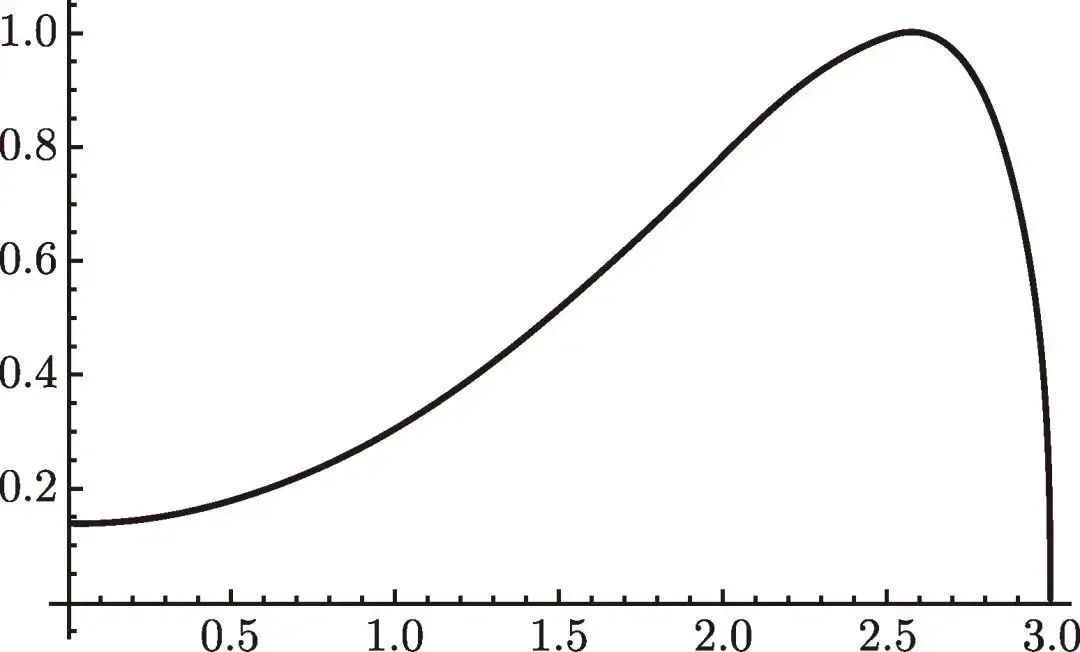
图 6.1
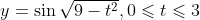
的图像
厄尔特曼坚持让学生每一次在选择时间区间的同时记录上界和下界, 也为最终引入极限播下了种子. 正如我们在第四章看到的, 现代意义下的极限是通过不等式来定义的。为了给
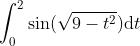
指定一个值, 就是断言任给两个数, 一个数比指定的数大, 另一个数比指定的数小, 我们可以选取充分小的区间段, 使得和式的值介于这两个数之间. 这恰好就是我们所指的定积分作为黎曼和的极限的含义。
在整本书中, 我都坚持将大多数学生记得 (如果他们记得) 的这个联系积分和微分的定理称为积分学基本定理, 而不是简单的微积分基本定理 (fundamental theorem of calculus). 正如我在 2.7 节脚注中所强调的, 这有历史渊源. 更重要的是, 其背后有更深层次的教学原因. 很多学生很快就忘记了积分的极限定义. 考虑到大多数课程将重点放在了积分的技巧, 而忽略了极限定义的应用, 大多数学生认为积分与求原函数就是一回事, 这一点毫不奇怪. 造成的结果是, 原本应该处于微积分中心地位的定理被简化为一句同义反复。
柯西第一个证明了这个定理, 他证明这个定理就是为了将积分的两种定义联系起来, 一个作为求和的极限, 另一个作为求原函数. 称之为积分学基本定理不仅更准确, 而且提醒我们这个定理的本质在于将对积分的两种不同理解联系起来. 它可以提醒学生, 积分不仅仅是简单的求原函数。
导数讲授为变化率
我们可以质疑, 公元 1000 年左右的古印度天文学家是否从现代意义上理解了正弦函数的导数. 不过, 他们研究变化率, 致力于理解输入的微小改变如何影响了输出的改变. 他们已经发现, 在正弦函数的情况下, 这个变化率是一个很容易计算的量, 并且可以用来估计输出的变化量. 比起切线的斜率来, 这是对导数的更直观的介绍. 此外, 它为将导数最终应用到下述情形准备好了基础, 在那些情形中, 我们只知道近似的输入值, 还需要控制住可能的输出值。
我们知道, 即便是微积分课堂上的学生, 理解变化率也很难, 但是他们一旦理解了变化率, 就为将导数理解为切线的斜率打好了扎实的基础. 当我在美国玛卡莱斯特学院教授大一新生第一学期的微积分课程时, 我的大多数学生已经多少见过微积分. 20 多年以来, 我的这门课一直以简单评估他们对微积分的了解为开头. 前两个问题就是问:

在

时的瞬时变化率是多少?

在区间

上的平均变化率是多少?每个稍微了解一点儿微积分的人都能回答前一个问题. 而这些学生几乎没有一个答得上来后一个问题. 许多人是对在

与

时的瞬时变化率做平均. 考虑到历史上理解瞬时速度的困难, 奇怪但真实的是, 比起平均速度来, 学生更适应瞬时速度。
我认为对此有一些解释. 第一个解释是, 平均变化率在微积分的先修课程中没有得到基本的强调. 虽然它出现在每一门微积分课程的入门素材中, 但很快就被忘记了, 因为学生的注意力转向了微分的种种技巧以及确定瞬时变化率的简单方法. 另一个解释是, 这个术语被称为“平均”. 但它看起来都不像学生在小学和中学学到的任何平均. 最后, 平均变化率是一个比值。
学生很难理解导数的极限定义的重要性. 如果我们试着向学生解释
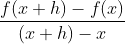
是从
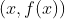
出发的一条割线的斜率, 而且当
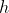
趋于 0 时, 就成为该点处切线的斜率, 我们所说的含义就在这些接踵而至的陌生概念中丢失了。
事实上, 我们可以从一个描述时刻
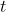
的累积量的函数出发, 并问它在
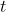
时刻的累积率是多少. 厄尔特曼让学生估计一支箭射出 2 秒以后的速度, 假定它在
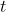
时刻的高度为 (图 6.2)
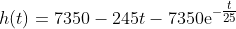
米/秒 .
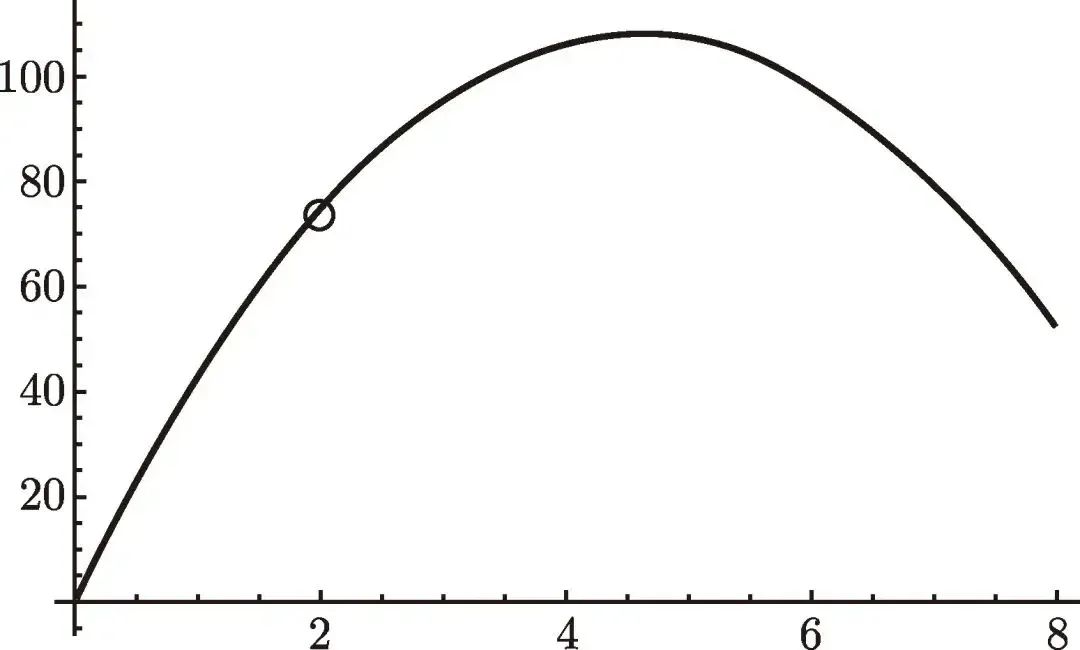
图 6.2
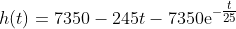
的图像
学生们被要求估计这个速度的上界与下界, 并且误差不超过 0.1 米/秒, 这使他们能够求出近似速度, 并给出近似值的误差范围。
导数的定义对于理解如何求近似变化率是很重要的. 对于在头一年的微积分课程里关于微分定理的证明, 导数的定义在某种程度上都是本质的. 但学生同时要对导数作为瞬时变化率有直观的理解, 即一个物体在给定时刻运动得有多快. 这就对第二章所强调的微分的另一个重要方面 —— 微分方程 —— 提供了自然的引导。
纳入纳皮尔在对数方面的工作的一个原因, 就是要强调他在关联变化率方面的工作. 事实上, 他得到了这样的结果, 若
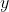
是
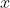
的对数, 则
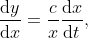
其中常数

依赖于对数的底. 不幸的是, 很少有微积分课讲述了微分方程的威力与重要性. 我喜欢麦克斯韦方程组的故事, 因为它诠释了我们如此关心微积分的一个原因, 在用数学模型来揭示这个世界的奥秘方面, 微积分具有难以预料的洞察威力. 许多革新的微积分课程, 包括最早的一些微积分改革课程, 以及我们目前在玛卡莱斯特学院开设的课程, 都是从微分方程开始的, 并且整个课程都在强调微积分可以建立动态模型. 再一次, 软件技术使得学生可以很容易地探究种种模型: 人口增长、流行病的传播、捕食者与被捕食者模型. 这为围绕微积分的学习提供了激动人心的课题. 对如何完成数值近似的分析架起了一座桥梁, 让导数回到变化率的极限。
导数是一个丰富的概念, 带来了众多新的理解. 但对许多学生来说, 他们唯一的收获就是将x^3变成3x^2, 这是何其不幸!
无穷级数讲授为部分和序列
大多数情况下, 微分约化为求导, 积分约化为求原函数, 无穷级数约化为判定敛散性. 其实无穷级数是关于部分和的一种比较差劲的观点, 因为很少有学生能记住他们曾背诵的收敛判别准则, 我非常赞同许多院校的做法, 先等到学生掌握了作为部分和的泰勒多项式, 然后再分析幂级数的收敛性.尽管很有挑战性, 我却乐于纳入拉格朗日余项定理作为控制误差的工具. 这也传递出了中值定理的实际重要性。
我还介绍了欧拉对指数函数的幂级数展开, 展示了无穷和带来的妙趣, 我希望我的学生们能够欣赏这个例子. 可以考虑让学生从复利公式
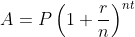
开始探究, 要求他们利用二项式定理展开, 然后探究当n增大时这个展开的性态如何, 让他们发现这个公式与指数函数之间的关联。
在学生的这个阶段, 虽然一般的幂级数不及泰勒多项式重要, 但常数项级数与几何级数非常重要. 在数学中, 几何级数几乎是无处不在的, 而且当学生学习种种收敛准则时, 几何级数是许多收敛准则的基石。
常数项级数很重要, 这是因为, 我们对极限的现代理解源于 18 世纪为理解它们收敛之含义所付出的努力. 科学家意识到, 关键的问题在于, 他们能否控制住部分和与所断言的值之间的差距. 与历史发展的路线一致, 许多教材选取无穷求和的例子来开始极限的学习。
此外, 学生需要意识到, 当莱布尼茨断言
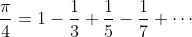
时是何其大胆. 对学生来说, 这里有个机会让他们弄明白, 这样一个等式的含义是什么. 讨论
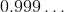
的含义自然融入该框架内。
极限讲授为不等式的代数
虽然在微积分课堂上给大一的学生讲授极限的

定义并要求他们掌握是不负责任的, 但这个形式化背后的思想对他们来说是可以接受的. 不论是积分、导数还是级数, 它们都是通过逼近来定义的. 极限是一个预先指定的值, 对任意的两个界, 一个比这个给定的值大, 另一个比这个给定的值小, 一旦我们限制区间的长度 (对积分和导数而言) 或部分和的最小项数 (对无穷级数而言), 总可以使得近似在这两个界之间。
在微积分中应用的极限的思想也许看起来很简单, 但事实上它可以相当复杂. 对学生理解方式的探究揭示出, 学生在理解极限思想时最常用的一个比喻是被研究者称为“坍塌”的比喻. 不论是以明确还是隐含的方式, 学生将
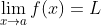
理解为, 当x越来越趋近于a时,
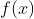
就越来越接近于L, 直到当x到达a时,
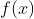
坍塌到L
对极限的大多数应用来说, 这个解释并不太坏, 而且常常被证明富有价值, 不过它也造成了一些危险的误导. 正如斯温亚德 (Swinyard)曾证明的, 这是对极限的一种“以x为先导”的视角, 考察自变量的变化如何影响因变量的变化. 问题在于, 极限的真正定义是“以y为先导”的, 先围绕y值选择一个可容许的误差, 然后确立存在x值的一个范围可以保证这一点. 斯温亚德和拉森 (Larsen)曾表明, 学生理解极限的正确定义有极大的困难, 直到他们转换到“以y为先导”的理解。
在英国数学家戴维·托尔 (David Tall)给 22 名数学专业的大四学生提出的下述问题中, 坍塌比喻也带来了困难。
若
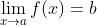 且
且 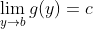 , 是否必然有
, 是否必然有 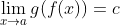 ?
?
即便在反复要求再次考虑答案以后, 22 名学生中仍然有 21 名坚持认为
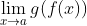
必定等于c。
正是关注“越来越接近”让他们误入歧途. 对
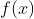
越来越接近b的理解自然引出这样的误解: 越来越接近b的变量y可以替换为
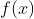
. 但如果
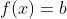
是一个常数函数, 而g在b处有极限但不连续, 即
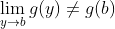
, 会发生什么呢?在这种情况下,
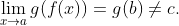
学生在理解
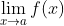
时经常忽视的一个细节是,x不能等于a, 而
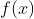
可以等于极限值. 注意, 这处于托尔的例子的核心. 当写
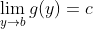
时, 我们在考虑变量y, 它是明确不等于b的. 但当我们写
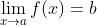
时, 并没有排除在a附近的x满足
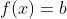
的可能性。
我们很自然会问, 为什么在定义a处的极限时, 要排除自变量等于a的情形?这是因为对于在a 处没有定义的函数, 我们也需要考虑其极限, 特别是在导数的定义中. 当

时, 平均变化率
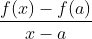
没有定义. 我们需要极限的一个定义, 它只要考虑
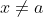
的情况。
厄尔特曼引导学生发现微分和积分原理的探究例子源于他对学生用来解释极限的“坍塌比喻”之分析.他发现, 对许多学生来说, 近似的语言是自然而高效的. 明确了这一点后, 他研发了许多任务, 要求学生将他们的近似思想系统化, 利用不等式的代数来预先指定近似导数或积分要达到的精度. 这让学生对这些概念有了切实的理解, 并为最终过渡到形式定义奠定了基础。
正如厄尔特曼在 2008 年报告的,不论是微分、积分还是级数, 在每一种背景下, 学生都必须回答五个关键问题:
(1) 你在对什么东西做近似?
(2) 近似是什么?
(3) 误差是什么?
(4) 误差的界是多少?
(5) 误差是否可以控制在任意预先指定的精度内?
如厄尔特曼所解释的, 最后两个问题其实是一对互逆的问题: 给定近似中所用参数的描述, 误差的界是多少?给定误差的界, 如何选取近似中的参数?
并非只有厄尔特曼采取了这个方法. 彼得·拉克斯 (Peter Lax) 和玛利亚·特雷尔 (Maria Terrell) 在其《微积分及其应用》(Calculus with Application) 的开篇以不等式的论述为开端, 对极限进行了仔细的介绍。
最后, 我要稍微讲一讲无穷小. 近一千年来以来, 它是富有成果的洞见的源泉. 无穷小仍然具有巨大的直观吸引力, 经常帮助科学家将累积问题转化为定积分, 帮助他们导出微分方程. 虽然基于无穷小的微积分可以严格化, 但那是一个需要成熟的集合论的 20 世纪的成果. 不过完全依赖于无穷小的主要问题在于, 过渡到对极限的现代理解将变得困难得多. 考虑到学生如此容易掌握近似和不等式, 这看起来是一个更自然且富有成果的途径。
审核编辑 :李倩
-
全美经典学习指导系列-微积分2008-08-08 0
-
微积分公式大全2010-01-25 0
-
谁有labview微积分的例子啊2011-09-23 0
-
求运放有微积分反馈的资料2013-05-29 0
-
分享《Matlab与微积分》课件2018-10-30 0
-
微积分pdf(全美经典)2008-08-08 3008
-
Matlab的微分、积分和微分方程2008-10-17 4583
-
RC微积分威廉希尔官方网站 的Multisim仿真2012-02-29 3477
-
微积分问题的计算机求解_中科院matlab课件2016-08-08 726
-
微积分(电子科技大学)2017-04-16 2881
-
深度学习中会用到的微积分知识2020-01-22 2541
-
深度解读你也能懂的微积分2020-06-28 6020
-
硬件设计为何还要学习微积分?2021-05-03 2520
-
Banach空间几类分数阶微积分方程的mild解的存在性2021-09-17 546
-
PyTorch教程22.4之多元微积分2023-06-06 253
全部0条评论

快来发表一下你的评论吧 !

