

机器学习笔记之优化-拉格朗日乘子法和对偶分解
电子说
描述
优化是机器学习中的关键步骤。在这个机器学习系列中,我们将简要介绍优化问题,然后探讨两种特定的优化方法,即拉格朗日乘子和对偶分解。这两种方法在机器学习、强化学习和图模型中非常流行。
优化问题
优化问题通常定义为:
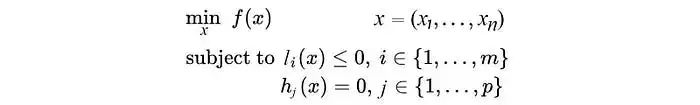
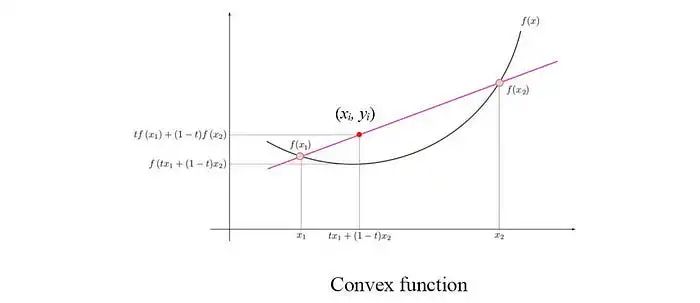
优化问题包含一个目标函数和可选的不等式和等式约束。一般的优化问题是NP难问题。但是,很多类别的凸优化问题可以在多项式时间内解决。当我们将f(x₁)和f(x₂)相连形成下方的红线时,如果f是一个凸函数,那么对于它们之间的点,红线总是在f的上方,即 yᵢ ≥ f(xᵢ)。
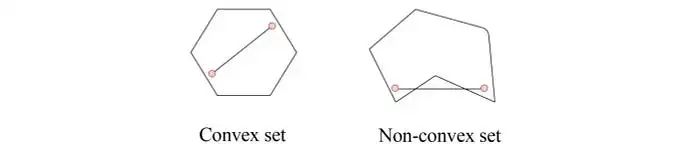
一个凸优化问题具有凸目标函数和凸可行集的特征。可行集是满足约束条件的x的集合。在凸集中,集合中两个点之间的任何值也必须属于凸集。
从另一个角度来看,在凸优化问题中,f和l是凸函数,
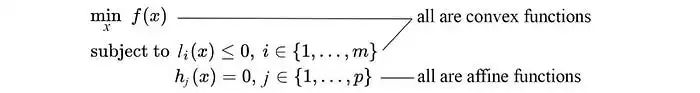
并且等式约束是仿射函数,其一般形式为:
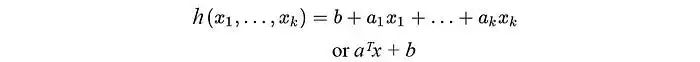
顺带一提,仿射函数是凸函数,这一点我们后面会用到。
在机器学习中,线性回归的目标函数通常表示为最小二乘误差。最小二乘优化问题已经得到广泛研究。有许多数值方法可以对它们进行求解,除非达到了某些可扩展性限制,否则它们可以通过解析方法(正规方程)解决。这在优化问题中是相对容易解决的问题。

否则,如果机器学习问题可以表示为线性规划问题,我们可以应用线性规划。这也已经得到了广泛的研究。线性规划中x的可行集是一个多面体。
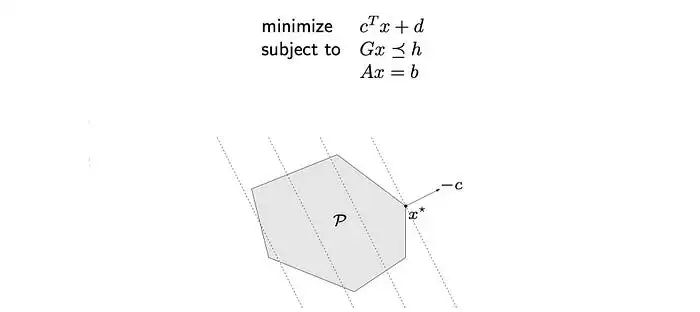
在我们上面的例子中,虚线是目标函数的等高线。最优解x*将是其中一个顶点。
一般来说,如果问题是凸优化问题,我们可以通过数值方法来解决。一个函数是凸函数,如果它的二阶导数对于所有x都是正的。
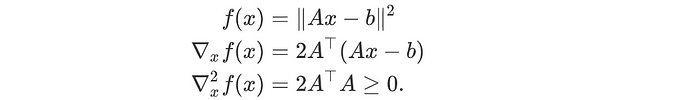
在机器学习中,我们经常将问题转换、近似或放宽为这些更简单的优化模型之一。
拉格朗日乘子
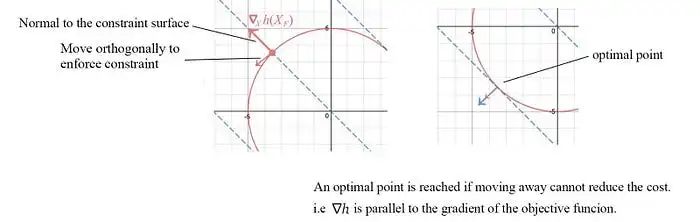
让我们专注于寻找一个一般优化问题的解。考虑代价函数为f=x+y,等式约束为h: x² + y² = 25,如下图所示的红色圆圈。
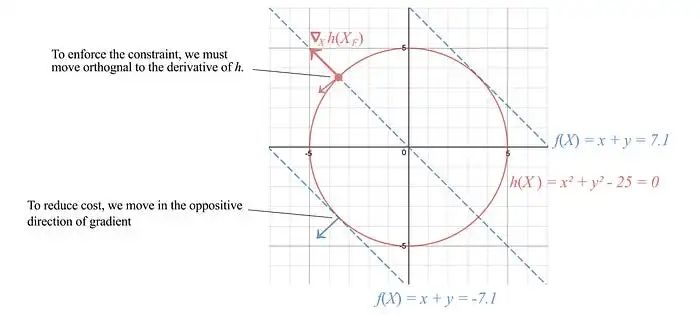
为了满足约束条件,我们沿着约束面法线的正交方向移动,即垂直于∇x h。为了降低代价,我们选择沿着f的负梯度方向移动。当我们无法进一步移动以降低代价时,就达到了最优点。这发生在∇h与代价函数的梯度对齐时。
i.e.,
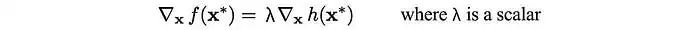
h(x) = 0也意味着-h(x) = 0。λ的符号取决于h的定义方式。因此,λ可以是正的、负的或零。
接下来,我们定义拉格朗日函数为:
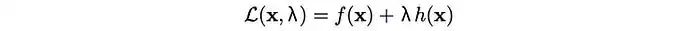
如果我们分别对拉格朗日函数关于x和λ求导,并将它们设置为零,如下所示,我们就可以强制执行前面描述的最优点以及等式约束。
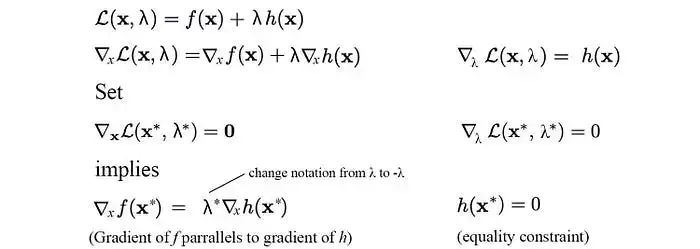
因此,通过找到关于x和λ的拉格朗日函数的最优点,我们可以确定在强制执行等式约束的情况下的最优解。我们也可以在拉格朗日函数中有多个约束和不等式约束。优化问题的形式将为:
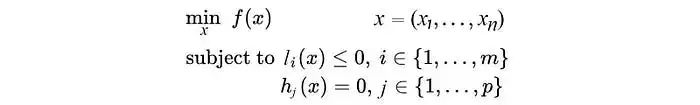
拉格朗日函数的定义如下:
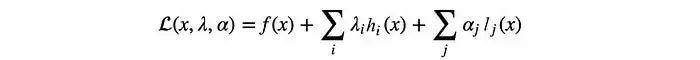
现在不等式约束要求最优点在阴影区域内(包括边界)。当解是最优时,f和l的梯度将具有相同的方向,即αᵢ ≥ 0。
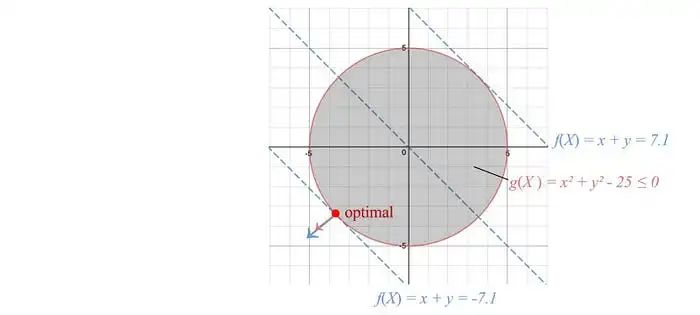
让我们再对不等式约束进行另一个观察。下面的左图表示一个具有最优解为该圆圈中心的代价函数f。
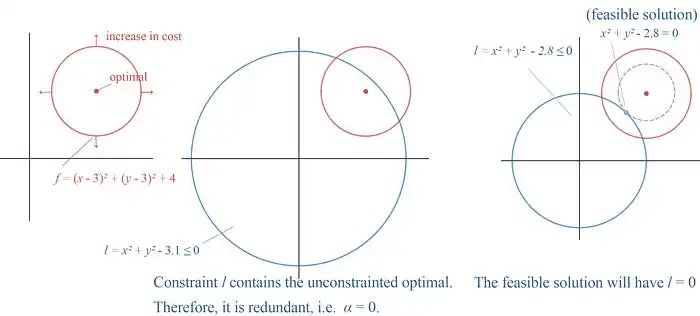
在中间的图中,我们为优化问题添加了一个不等式约束。但是,这个约束是多余的,因为无约束最优点已经满足这个约束条件。因此,αᵢ可以简单地为零,表示它是多余的。
在右边的图中,无约束最优解落在l的外面。我们必须增加代价(红色圆圈)直到它与l相交。对应的最低代价将使得约束l等于0。
因此,αᵢ lⱼ(x) 总是等于0。
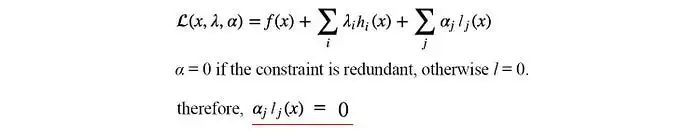
例子
让我们最大化f(x, y) = x + y,满足x² + y² = 32。
拉格朗日函数为:
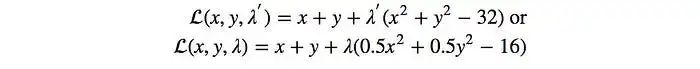
为了解决这个优化问题,我们需要分别对
-
Matlab采用障碍法及原对偶内点法解决不等式约束凸优化程序2012-03-06 0
-
机器学习基础|深入理解拉格朗日乘子法2017-12-13 0
-
《概率机器人》第I部分和第II部分学习笔记2019-04-26 0
-
拉格朗日乘子法和KKT条件相关知识概述2019-07-03 0
-
凸优化第二章之26对偶锥与广义不等式2020-05-08 0
-
机器学习基石笔记2020-05-26 0
-
吴恩达机器学习笔记分享2020-06-05 0
-
机器学习笔记之BP推导2020-06-15 0
-
如何搞定机器学习中的拉格朗日?看看这个乘子法与KKT条件大招2017-12-06 1083
-
机器学习的个人学习笔记2021-03-01 938
-
python机器学习笔记资料免费下载2021-03-01 1107
-
OpenStack之Cinder学习笔记2021-09-23 704
-
ROS 学习笔记之五:对Arduino环境刮目相看2021-11-29 515
-
支持向量机(原问题和对偶问题)2023-05-25 1361
-
PyTorch教程12.1之优化和深度学习2023-06-05 324
全部0条评论

快来发表一下你的评论吧 !

