鲸鱼优化算法MATLAB实战

一、鲸鱼优化算法

鲸鱼优化算法(Whale Optimization Algorithm,WOA)是模仿自然界中鲸鱼捕食行为的新型群体智能优化算法。它通过对自然界中座头鲸群体狩猎行为的模拟，通过鲸鱼群体搜索、包围、追捕和攻击猎物等过程实现优时化搜索的目的。鲸鱼优化算法的工作原理如下：

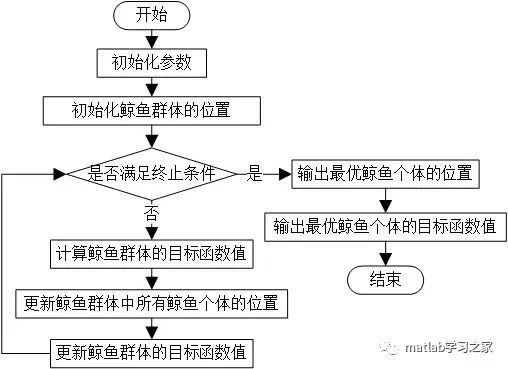
1、初始化：首先，在算法开始时，需要为每个鲸鱼设定一个初始位置，并生成初始种群。

2、搜索：每个鲸鱼都会按照一定的规则探索空间。这个过程可以模拟鲸鱼包围、追捕和攻击猎物等过程。

3、评估：每当鲸鱼移动的时候，都会对当前的鲸鱼种群计算适应度值。如果当前的适应度值优于之前的适应度值，则将当前适应度值设为最优解。

4、更新：当所有的鲸鱼都完成了移动和评估后，算法会更新所有鲸鱼的位置，并重复以上步骤。

5、迭代：鲸鱼优化算法可以进行多次迭代，直到找到最优解为止。

鲸鱼优化算法的优势在于操作简单，调整的参数少以及跳出局部最优的能力强，它能够快速找到最优解，并且对于各种类型的优化问题都能有效地工作。对于基础的问题，它还具有很好的收敛性和稳定性。

鲸鱼优化算法主要包括三个过程：1）包围猎物；2）发泡网攻击；3）搜索捕食。

鲸鱼优化算法的流程图如下图所示:

二、代码实战

%_________________________________________________________________________%
%  Whale Optimization Algorithm (WOA) source codes demo 1.0               %
%                                                                         %
%  Developed in MATLAB R2011b(7.13)                                       %
%                                                                         %
%  Author and programmer: Seyedali Mirjalili                              %
%                                                                         %
%         e-Mail: ali.mirjalili@gmail.com                                 %
%                 seyedali.mirjalili@griffithuni.edu.au                   %
%                                                                         %
%       Homepage: http://www.alimirjalili.com                             %
%                                                                         %
%   Main paper: S. Mirjalili, A. Lewis                                    %
%               The Whale Optimization Algorithm,                         %
%               Advances in Engineering Software , in press,              %
%               DOI: http://dx.doi.org/10.1016/j.advengsoft.2016.01.008   %
%                                                                         %
%_________________________________________________________________________%


% You can simply define your cost in a seperate file and load its handle to fobj 
% The initial parameters that you need are:
%__________________________________________
% fobj = @YourCostFunction
% dim = number of your variables
% Max_iteration = maximum number of generations
% SearchAgents_no = number of search agents
% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n
% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n
% If all the variables have equal lower bound you can just
% define lb and ub as two single number numbers


% To run WOA: [Best_score,Best_pos,WOA_cg_curve]=WOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj)
%__________________________________________


clear all 
clc


SearchAgents_no=30; % Number of search agents


Function_name='F1'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper)


Max_iteration=500; % Maximum numbef of iterations


% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);


[Best_score,Best_pos,WOA_cg_curve]=WOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);


figure('Position',[269   240   660   290])
%Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])


%Draw objective space
subplot(1,2,2);
semilogy(WOA_cg_curve,'Color','r')
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');


axis tight
grid on
box on
legend('WOA')


display(['The best solution obtained by WOA is : ', num2str(Best_pos)]);
display(['The best optimal value of the objective funciton found by WOA is : ', num2str(Best_score)]);

%_________________________________________________________________________%
%  Whale Optimization Algorithm (WOA) source codes demo 1.0               %
%                                                                         %
%  Developed in MATLAB R2011b(7.13)                                       %
%                                                                         %
%  Author and programmer: Seyedali Mirjalili                              %
%                                                                         %
%         e-Mail: ali.mirjalili@gmail.com                                 %
%                 seyedali.mirjalili@griffithuni.edu.au                   %
%                                                                         %
%       Homepage: http://www.alimirjalili.com                             %
%                                                                         %
%   Main paper: S. Mirjalili, A. Lewis                                    %
%               The Whale Optimization Algorithm,                         %
%               Advances in Engineering Software , in press,              %
%               DOI: http://dx.doi.org/10.1016/j.advengsoft.2016.01.008   %
%                                                                         
%                                                                         %
%_________________________________________________________________________%




% The Whale Optimization Algorithm
function [Leader_score,Leader_pos,Convergence_curve]=WOA(SearchAgents_no,Max_iter,lb,ub,dim,fobj)


% initialize position vector and score for the leader
Leader_pos=zeros(1,dim);
Leader_score=inf; %change this to -inf for maximization problems




%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);


Convergence_curve=zeros(1,Max_iter);


t=0;% Loop counter


% Main loop
while t< Max_iter
    for i=1:size(Positions,1)


        % Return back the search agents that go beyond the boundaries of the search space
        Flag4ub=Positions(i,:) >ub;
        Flag4lb=Positions(i,:)< lb;
        Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;


        % Calculate objective function for each search agent
        fitness=fobj(Positions(i,:));


        % Update the leader
        if fitness< Leader_score % Change this to > for maximization problem
            Leader_score=fitness; % Update alpha
            Leader_pos=Positions(i,:);
        end


    end


    a=2-t*((2)/Max_iter); % a decreases linearly fron 2 to 0 in Eq. (2.3)


    % a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)
    a2=-1+t*((-1)/Max_iter);


    % Update the Position of search agents 
    for i=1:size(Positions,1)
        r1=rand(); % r1 is a random number in [0,1]
        r2=rand(); % r2 is a random number in [0,1]


        A=2*a*r1-a;  % Eq. (2.3) in the paper
        C=2*r2;      % Eq. (2.4) in the paper




        b=1;               %  parameters in Eq. (2.5)
        l=(a2-1)*rand+1;   %  parameters in Eq. (2.5)


        p = rand();        % p in Eq. (2.6)


        for j=1:size(Positions,2)


            if p< 0.5   
                if abs(A) >=1
                    rand_leader_index = floor(SearchAgents_no*rand()+1);
                    X_rand = Positions(rand_leader_index, :);
                    D_X_rand=abs(C*X_rand(j)-Positions(i,j)); % Eq. (2.7)
                    Positions(i,j)=X_rand(j)-A*D_X_rand;      % Eq. (2.8)


                elseif abs(A)< 1
                    D_Leader=abs(C*Leader_pos(j)-Positions(i,j)); % Eq. (2.1)
                    Positions(i,j)=Leader_pos(j)-A*D_Leader;      % Eq. (2.2)
                end


            elseif p >=0.5


                distance2Leader=abs(Leader_pos(j)-Positions(i,j));
                % Eq. (2.5)
                Positions(i,j)=distance2Leader*exp(b.*l).*cos(l.*2*pi)+Leader_pos(j);


            end


        end
    end
    t=t+1;
    Convergence_curve(t)=Leader_score;
    [t Leader_score]
end

实验结果：