

RF通信的数字预失真:从等式到实现方案
描述
本文介绍数字预失真(DPD)的数学基础知识,以及它如何在收发器的微处理器和硬件中实现。阐述为何现代通信系统需要DPD,并探讨如何通过数学模型捕捉现实世界的信号失真。
简介
DPD是数字预失真的首字母缩写,许多射频(RF)工程师、信号处理爱好者和嵌入式软件开发人员都熟悉这一术语。DPD在蜂窝通信系统中随处可见,使功率放大器(PA)能够有效地为天线提供最大功率。随着5G使基站中的天线数量增加,频谱变得更加拥挤,DPD开始成为一项关键技术,支持开发经济高效且符合规格要求的蜂窝系统。
对于DPD,无论从纯粹的数学角度出发,还是在微处理器上实现更受限制,我们许多人都有自己独特的见解。您可能是负责评估RF基站产品中DPD性能的工程师,或者是一名算法开发人员,很想知道数学建模技术在实际系统中的实现方式。本文旨在拓宽您的知识面,帮助您从各个角度全面了解这个主题。
什么是DPD?为什么要使用DPD?
当基站射频装置输出RF信号时(参见图1),需要先将其放大,然后再通过天线发射。我们使用RF PA来执行此操作(放大)。在理想情况下,PA接收输入信号,然后输出与其输入成正比的更高功率信号。在执行此操作期间,PA会尽可能保持高能效,将提供给放大器的大部分直流电源都转化为信号输出功率。
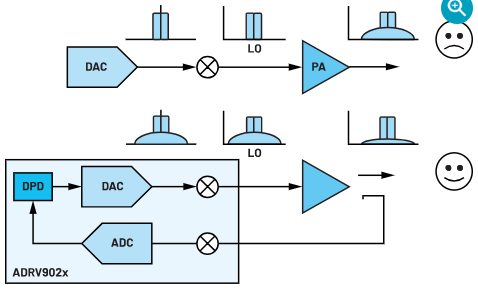
图1.采用和未采用DPD技术的简化射频结构框图。
但这不是一个理想的世界。PA由晶体管构成,晶体管是有源器件,本身具有非线性。如图2所示,如果我们在其“线性”区域使用PA(这里的线性是相对而言;所以加了引号),则输出功率与输入功率相对成比例。此方法的缺点是PA的使用效率通常很低,提供的大部分功率都会作为热量流失。我们通常希望在PA开始压缩时使用。这意味着,如果输入信号增加了设定量(例如3 dB),PA输出不会增加同样的量(可能只增加1 dB)。很显然,此时放大器使信号严重失真。
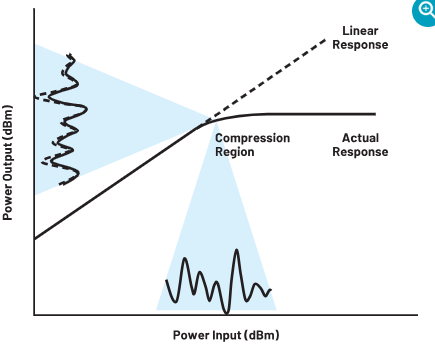
图2.PA输入功率与输出功率之间的关系图(显示了样本输入/输出信号的投影)。
这种失真发生在频域中的已知位置,具体取决于输入信号。图3显示了这些位置,以及基频与这些失真产物之间的关系。在RF系统中,我们只需要对基波信号附近的失真进行补偿,这些信号是奇阶交调产物。系统滤波处理带外产物(谐波和偶阶交调产物)。图4显示RF PA的压缩点附近的输出。交调产物(特别是三阶)清晰可见,就像是围绕着目标信号的“裙摆”。
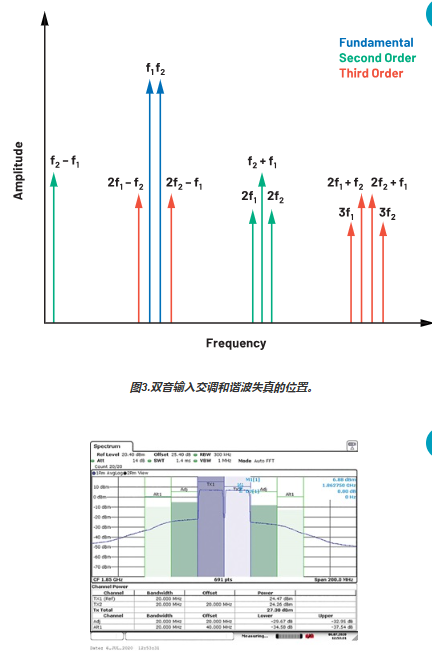
图4.2× 20 Mhz载波通过SKY66391-12 RF PA。中心频率 = 1850 MHz。
DPD旨在通过观察PA输出来表征这种失真,要了解所需输出信号,随之更改输入信号,使得PA输出接近理想值。只有在相当具体的情况下才能有效地实现这一目标。我们需要配置放大器和输入信号,使放大器有一定程度的压缩但未完全饱和。
PA失真建模背后的数学计算
看到希腊字母和其他数学符号,会不会让人想起过去可怕的大学考试?不止是您如此!如果大家得到的首批参考资料中有一份是涉及很多数学知识的学术论文,那么很可能会打退堂鼓,不想去看它。这篇论文 “射频功率放大器数字预失真的广义记忆多项式模型”1 具有开创性,它介绍了针对DPD广泛使用的广义记忆多项式(GMP)方法。如果您只涉足信号处理方面的工作,上述主题内容对您而言可能有点深奥。所以,我们先尝试拆解一下GMP方法,以更直观地了解数学在其中的作用。
Volterra级数是DPD的重要数学基础,它用于建立具有记忆的非线性系统模型。记忆仅仅意味着系统的当前输出取决于当前和过去的输入。Volterra级数很常用(所以功能强大),在电气工程以外的许多领域都有使用。对于PA DPD,Volterra级数可以精简使用,使其在实时数字系统中更易实现,也更稳定。GMP就是这样一种精简方法。
图5显示如何使用GMP对PA的输入x和输出y之间的关系进行建模。可以看到,该等式的三个单独的求和块彼此都非常相似。我们先来看看下方用红色圈出来的第一个。|x(…)|k项是指输入信号的包络,其中k是多项式阶。l将记忆集成到系统中。如果La = {0,1,2},那么该模型允许输出yGMP (n)由当前的输入x(n)和过去输入x(n – 1)和x(n – 2)决定。图6分析多项式阶k对样本向量的影响。向量x是单个20 MHz载波,在复基带上表示出来。去除记忆部分,以简化GMP建模等式。x|x|k图显示的失真与图4中的实际失真非常相似。
每个多项式阶(k)和记忆延迟(l)都有相关的复值权重(akl)。在选择模型的复杂程度之后(其中包括k和l的值),需要根据已知输入信号的PA输出实际观测值来求解这些权重。图7将简化的等式转换为矩阵形式。可以使用数学符号简明表示该模型。但是,要在数字数据缓冲区实现DPD,用矩阵表示法会更简单,也更具代表性。
我们来看看图6中等式的第二行和第三行,为了简化,这两行被忽略了。注意,如果m设置为0,那么这两行会变得与第一行一模一样。这些行允许在包络项和复基带信号之间增加延迟(正延迟和负延迟)。这些称为滞后交叉和超前交叉项,可以显著提高DPD的建模精度。在我们尝试对放大器的行为建模时,这些项提供了额外的自由度。注意,Mb、Mc、Kb和Kc不包含0;否则,会重复第一行的项。
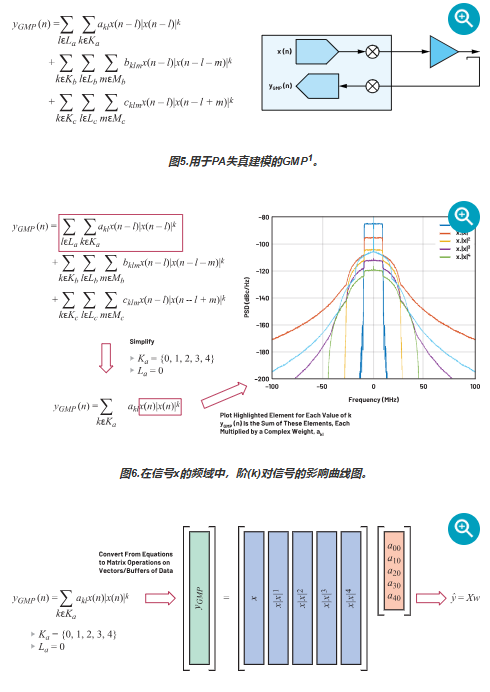
图7.将简化的等式转换为数据缓冲区的矩阵运算(更接近于数字实现方式)。
那么,我们如何确定模型的阶、记忆项的数量,以及应该添加哪些交叉项?此时,就需要一定数量的“黑魔法”了。我们掌握的关于失真的物理学知识能够提供一定帮助。放大器的类型、制造材料,以及通过放大器的信号带宽都会影响建模项,可以帮助熟悉该领域的工程师确定应该使用哪个模型。但是,除此之外,还涉及一定程度的反复试验。
现在有了模型架构,我们从数学角度来解决该问题的最后一个方面是如何求解权重系数。在实际场景中,人们倾向于求解上述模型的倒数。事实证明,这些模型系数能够彼此互惠,可以使用相同的权重对捕捉到的PA输出向量进行后失真,以消除非线性,并对通过PA发送的发射信号预失真,使得PA输出尽可能呈现线性。在图8所示的框图中,显示了如何对权重系数进行估算和预失真。
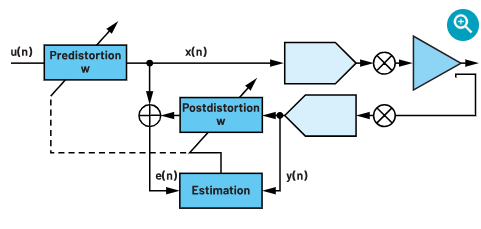
图8.建模和预失真间接实现框图。
在逆模型中,将图7给出的矩阵等式互换,给出X̂ = Yw。其中,矩阵Y的构成方式与其他示例中X的构成方式相同,如图9所示。在本例中,包含了一个记忆项,且减少了包含的多项式的阶数。为了求解w,我们需要得出Y的倒数。Y不是方形的(是一个瘦长矩阵),所以需要使用“伪逆”矩阵进行求解(参见等式1)。这是从最小二乘意义上求解w,也就是说,最小化了X̂和Yw之间的差的平方,正合我们的心意!

鉴于是在具有不同信号的真实环境中使用,我们可以对其进一步优化。在这里,系数是基于之前的值进行更新,因此受到限制。μ是0和1之间的常数值,用于控制每次迭代时权重的变化量。如果μ = 1,w0 = 0,那么此等式立即恢复到基本最小二乘解。如果将μ设为小于1的值,则需要多次迭代才能使系数收敛。
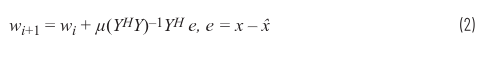
注意,这里描述的建模和估算技术并非是执行DPD的唯一方式。也可以使用其他技术,例如基于动态偏差减少的建模来代替或作为附加方法使用。上述用于求解系数的估算技术具有多种实现方式。鉴于本文篇幅短小,并非书籍,所以此处不再赘述。
如何在微处理器中实现这一技术?
我们前面介绍了相关数学知识。下一个问题:如何在实际通信系统中进行应用?它在数字基带中实现,一般在微处理器或FPGA中实现。ADI的RadioVerse®收发器产品(例如ADRV902x系列)内置微处理器内核,其结构有助于轻松实现DPD。
图9.以矩阵形式表示的逆算法等式。有些记忆包含在其中。
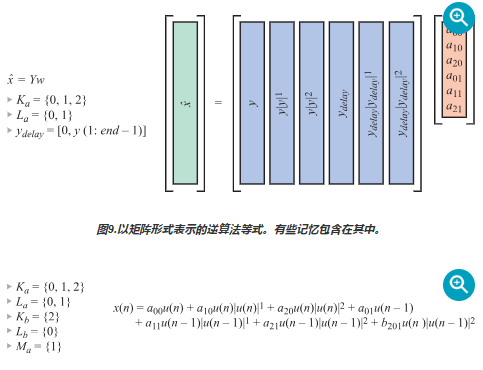
图10.具有一次记忆选择和一个三阶交叉项元素的三阶预失真计算案例。
在嵌入式软件中实现DPD涉及两个方面。一是DPD执行器,对实时发送的数据执行实时预失真,二是DPD自适应引擎,基于观察到的PA输出来更新DPD系数。
对于如何在微处理器或类似器件中实时执行DPD和许多其他信号处理概念,关键在于使用查找表(LUT)。LUT允许用更简单的矩阵索引操作来代替成本高昂的运行时计算。我们来看看DPD执行器如何对发送的数据样本应用预失真。代表符号如图8所示,其中u(n)表示要传输的新数据样本,x(n)表示预失真版本。图10显示在给定场景下,获取一个预失真样本所需的计算。这是一个相对受限的示例,最高多项式阶为三阶,只有一次记忆选取和一个交叉项。即使在这种情况下,要获取这样一个数据样本,也需要进行大量乘法、幂运算和加法运算。
在这种情况下,使用LUT可以减轻实时计算负担。可以将图10所示的等式改写成图11所示的样式,其中输入LUT的数据会变得更加明显。每个LUT都包含等式中突出显示项的结果值,它们对应|u(n)|的多个可能值。分辨率取决于在可用硬件中实现的LUT大小。当前输入样本的幅度大小基于LUT的分辨率进行量化,可以作为索引,用于访问给定输入的正确LUT元素。
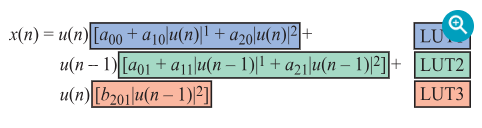
图11.对等式项重新分组,以显示LUT的结构。
图12显示如何将LUT集成到我们示例案例的完全预失真执行器实现方案。注意,这只是其中一种可能的实现方法。在仍然保持相同输出的情况下,可以做出更改,例如:可以将延迟元素z–1移动到LUT2右侧。
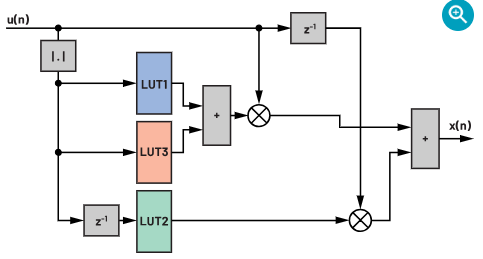
图12.使用LUT可能实现DPD的框图。
自适应引擎负责求解用于计算执行器中的LUT值的系数。这涉及到求解等式1和2中描述的w向量。伪逆矩阵运算(YH Y)-1 YH会耗费大量计算资源。等式1可以改写为

因为L和LH分别是上、下三角矩阵,所以花费很少的计算资源,就可以求解等式5和等式6,得出w。自适应引擎每次运行,得出w的新值时,都需要更新执行器LUT来体现这一点。根据观察到的PA输出,或者操作员掌握的待传输信号的变化情况,自适应引擎可以按照设定的定期间隔或不规则的间隔执行操作。
在嵌入式系统中实现DPD需要进行大量检查和平衡,以确保系统的稳定性。最重要的是,发送数据缓冲器和捕捉缓冲器数据的时间要一致,以确保它们之间建立的数学关系是正确的,且在长时间之后仍然保持正确。如果这种一致性丧失,那么自适应引擎返回的系数将不能对系统执行正确的预失真,可能导致系统不稳定。还应检查预失真执行器输出,确保信号不会使DAC饱和。
结论
本文从基础数学的角度研究DPD及其在硬件中的实现方法,希望借此揭示关于DPD的一些奥秘。本文对该主题的探讨只是冰山一角,可能有助于推动读者进一步研究通信系统中信号处理技术的应用情况。Pratt和Kearney的研究是关于在有线通信系统超宽带宽用例中使用DPD的一个不错的参考资料。2ADI的RadioVerse收发器产品可以集成DPD这类算法,为客户提供高度集成的RF硬件和可配置的软件工具。
审核编辑:郭婷
-
数字预失真解决方案2021-04-22 565
-
可修正RF信号的RF预失真2011-08-02 0
-
用于3G基站的ISL5239数字预失真威廉希尔官方网站2018-11-26 0
-
基于数字预失真线性化实现宽带功率放大器2019-06-25 0
-
如何对数字预失真平台系统进行仿真测试?2021-04-21 0
-
数字预失真如何改善数字信号发生器的失真性能?2021-05-06 0
-
模拟预失真芯片简化线性功放设计2011-06-23 1245
-
DSP+GC5322实现数字预失真系统2011-10-17 2792
-
数字预失真(DPD)算法研发工具和验证方案2012-02-14 1791
-
基于DSP的数字预失真系统设计方案2017-10-31 925
-
插入式短波预失真器的设计与实现2018-01-18 795
-
关于S信号源与频谱仪的宽带数字预失真算法研究的分析和介绍2019-10-12 3992
-
线性化技术和RF预失真器调谐实现最大的PA效率2021-05-21 6497
-
关于数字预失真的数学计算及实现方法2022-05-11 6681
-
使用RF PA线性化器优化功率放大器的预失真2023-01-05 3180
全部0条评论

快来发表一下你的评论吧 !

