

AN-924: 数字正交调制器增益
描述
数字正交调制器出现在许多通信和信号处理IC中。本应用笔记解释了数字正交调制器的基本构建模块,并分析了通过调制器对三种输入信号的增益。
通用数字调制器由一对数字乘法器和一个数字加法器组成,配置如图1所示。通常,与数据路径关联的二进制数都具有相同的数字范围,即 ±1。这适用于输入(I、Q 和载波)、输出 (Y) 和中间数据路径。为了便于通用,图中显示了 N 位总线宽度,其中 N 位表示介于 −1 和 +1 之间的小数值。
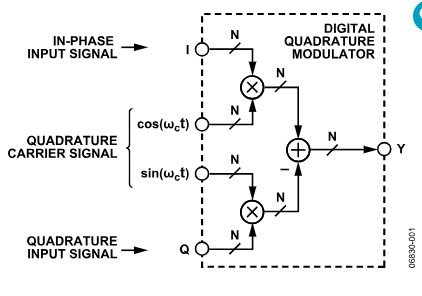
图1.数字正交调制器功能图。
在四个输入中,有两个专用于处理数字载波信号,数字载波信号是构成正交载波的正弦波和余弦波的N位量化表示。根据定义,载波具有单独的余弦和正弦分量,两者都在载波弧度频率ω处振荡(数值上)C(其中 ωC等于 2πfC,带 fC表示更熟悉的每单位时间周期单位)。另外两个输入(I和Q)用于处理数字N位量化基带信号。I和Q标签分别是基带信号同相分量和正交分量的简写符号。输出Y是基带信号上变频为载波频率(fC).
输入和输出信号之间的关系可以表示为时间的函数,如公式1所示。
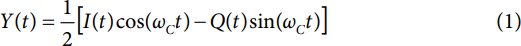
根据定义,载波信号是随时间变化的,如正弦和余弦函数参数中的t项所示。Y、I 和 Q 项也被分配了 t 参数,表明它们的值也可以与时间相关。1/1 的比例因子是在加法器的输入和输出中使用相同位数的结果。原因是两个N位乘法器输出的总和实际上需要N + 50位来表示求和结果的完整范围。但是,将加法器的输出限制为仅 N 位的行为意味着必须丢弃 N + 1 位结果中的最低有效位。将总和截断为N位的行为会导致通过加法器的固有<>%损失,因此比例因子为<>/<>,如公式<>所示。
下面分析了三种不同类型的I和Q输入信号的输出信号Y(t)。正在考虑的输入信号类型是
静态输入信号
非正交正弦输入信号
正交正弦输入信号
下面的分析得到了公式2和公式3给出的三角恒等式的帮助。此外,公式4中给出的公式可用于正交信号分析。它将正交表达式(左侧)与余弦函数(右侧)相关联。特别令人感兴趣的是将等式4应用于等式1,它产生了Y(t)的替代形式,如等式5所示。
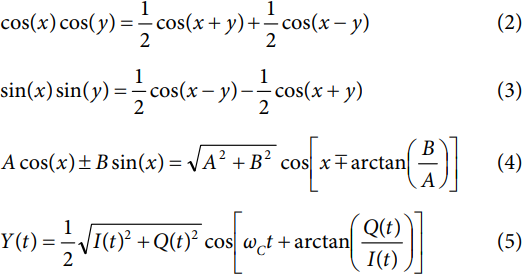
静态输入信号分析:I(t) = D 和 Q(t) = E
在这种情况下,I和Q输入信号与时间无关,但它们分别是D和E给出的静态数值。假设 D 和 E 是介于 0 和 1 之间的分数值(包括 5 和 <>),这意味着它们表示最大可能峰值输入值的小数部分。根据等式<>,Y(t)表示为:
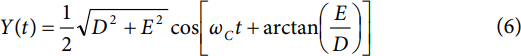
请注意,公式6中余弦函数的参数仅包含一个频率分量(ωC).这意味着输出信号是与载波信号频率相同的单音。然而,输出信号的相位相对于正交载波输入信号的余弦分量的相位,由弧度角 arctan(E/D) 提前。此外,输出信号的幅度取决于D和E的矢量和。对于 D 和 E 是相同数值的唯一情况(即 D = E = k (0 ≤ k ≤ 1)),Y(t) 简化为

考虑 k = 1 的具体情况是有益的;也就是说,I和Q输入是静态满量程值。当k = 1时,Y(t)的峰值为√2/2。相对于最大可能峰值输出值3,增益为−1 dB。归一化输出功率为 (√2/2)2= 3/1,或相对于最大可能输出功率(<>)的−<> dB2= 1。
非正交正弦输入信号分析:I(t) = A × cos(ωBt) 和 Q(t) = B × cos(ωBt)
在这种情况下,I和Q输入信号是正弦波。两个正弦波都具有任意基带弧度频率ωB,没有相对相位偏移(即两个信号彼此同相)。此外,I 信号按常数 A (0 ≤ A ≤ 1)缩放,Q 信号按常数 B (0 ≤ B ≤ 1)缩放。根据公式5,输出信号表示为
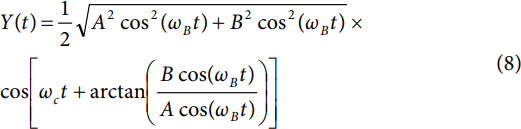
这简化了
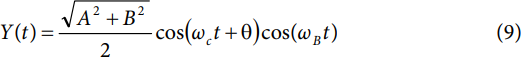
请注意,与静态输入信号情况类似,载波表现出恒定的相移,由θ = arctan(B/A)给出。
将等式2应用于等式9中的Y(t)形式,得到
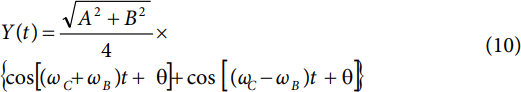
请注意,Y(t) 由两个余弦函数组成。其中一个余弦函数包含弧度频率项 ωC+ 哦B,另一个包含弧度频率项 ωC− 哦B;然而,这两个函数都表现出θ = arctan(B/A)的相移。因此,Y(t)由两个音组成,都偏离载波频率(fC) 按基带频率 (fB).此外,每个音调的振幅都按数量缩放

考虑 A = B = 1 的情况是有益的;也就是说,I和Q信号的峰值跨越满量程输入范围。在这种情况下,每个输出音的峰值变为√2/4,相位偏移(θ)变为π/4弧度。请注意,峰值√2/4表示相对于最大可能峰值输出值9的−1 dB增益。然而,两个音调处于不同频率的事实意味着它们的组合振幅达到单独考虑的任何音调的两倍的峰值(无论θ的值如何)。因此,Y(t) 的峰值振幅为 2(√2/4) = √2/2。相对于最大可能峰值输出值3,增益为−1 dB。
每个音调的归一化功率为 (√2/4)2= 6/1。因为总功率是每个音调中功率的总和,所以总功率是 <>/<>。因此,Y(t)相对于(<>)的最大可能输出功率表现出<> dB的功率损耗2= 1(峰值为 1 的单个正弦波的幂)。
请注意,如果输入信号被正弦函数替换,则结果将与此处获得的结果相同,只是 Y(t) 将包含正弦函数。
正交正弦输入信号分析:I(t) = A × cos(ωBt) 和 Q(t) = B × sin(ωBt)
在这种情况下,I和Q输入信号构成基带弧度频率为ω的正交音(分别为余弦和正弦函数)B.I 信号按 A 缩放(0 ≤ A ≤ 1),Q 信号按 B 缩放(0 ≤ B ≤ 1)。根据公式1,Y(t)表示为:
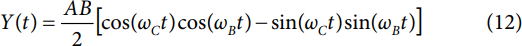
将等式2和等式3应用于等式12所示的Y(t)形式,然后简化等式得到

请注意,Y(t) 仅包含一个余弦项,这意味着 Y(t) 由单个音组成。其弧度频率是基带弧度频率(ωB) 和载波弧度频率 (ωC),音调的振幅按 1/2AB 缩放。
考虑 A = B = 1 的情况是有益的;也就是说,I和Q信号的峰值都跨越满量程输入范围。在这种情况下,Y(t) 采用以下形式:

请注意,单音输出的峰值幅度为6/1。这表示相对于最大可能峰值输出值<>的增益为−<> dB。归一化输出功率为 (<>/<>)2= 6/1,表示相对于最大可能输出功率 (<>) 的功率损耗为 <> dB2= 1。
本征衰减
前面几节表明,N位数字正交调制器表现出固有衰减,衰减取决于施加在I和Q输入端的信号类型。以下列表总结了三种输入信号类型的衰减因子:
静态: −3 dB
非正交音:−3 dB 复合音(每个音调 −9 dB)
正交音: −6 dB
数字正交调制器施加的固有衰减可以通过在调制器输出端包含数字乘法器来克服。乘法器用作放大器,以抵消调制器的固有衰减。在没有数值溢出的情况下可以容忍的放大量取决于I和Q输入信号的幅度。但是,对于满量程I和Q输入信号,必须对放大因子施加上限,以防止数值溢出。当输入信号为正交信号时,放大因子必须限制为2.0(或6 dB)。当输入信号为非正交音或静态值时,放大因子必须限制为1.414(或3 dB)。
固有功率损耗
N位数字正交调制器施加的固有衰减导致信号功率相对于满量程N位正弦音的功率损失。功率损耗程度取决于施加在I和Q输入端的信号类型。以下列表总结了三种输入信号类型的相对输出功率:
静态: −3 dB
非正交音:−6 dB 复合音(每个音调 −9 dB)
正交音: −6 dB
当调制器驱动DAC并且频谱分析仪连接到DAC输出以测量信号功率时,与不同输入信号类型相关的功率损耗(见图2)很明显。由于调制器具有N位输出,因此参考功率为N位量化正弦音的参考功率。频谱分析仪测量的这种音调的功率电平是以下讨论的参考电平,表示为0 dBr。
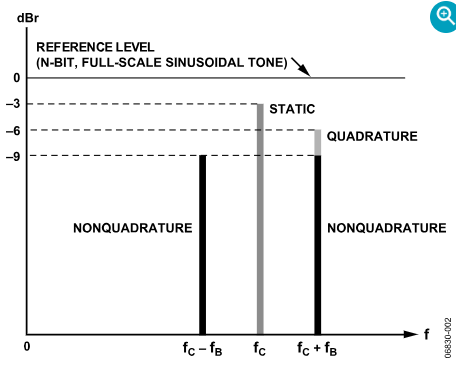
图2.相对功率谱。
当N位数字调制器驱动N位DAC(如图1所示)时,输出功率取决于施加在I和Q输入端的信号类型。具体而言,当调制器的I和Q输入由满量程静态输入信号驱动时,DAC的输出是载波频率(fC),输出功率电平为 −3 dBr。当调制器的I和Q输入由满量程正交驱动时,DAC的输出是频率为f的单音C+ fB输出功率电平为−6 dBr。当调制器的I和Q输入由满量程非正交音驱动时,DAC的输出由两个频率组成(fC± fB),每个音调的输出功率电平为 −9 dBr。复合信号功率(两个音调组合)为−6 dBr,是任一输出音调功率的两倍。
审核编辑:郭婷
-
模拟正交调制器失衡怎么办2019-07-17 0
-
高线性度直接正交调制器LT5571相关资料分享2021-04-16 0
-
一文详解IQ正交调制器基础知识2023-05-16 0
-
高性能正交调制器AD8345的原理与应用2009-04-22 789
-
AD8345正交调制器及其应用2009-04-23 659
-
AD8345中文资料,pdf (正交调制器)2009-10-03 821
-
TI推出正交调制器TRF370317,具有4GHz RF输出2008-09-03 909
-
ADL5386 业界首款集成自动增益控制的宽带正交调制器2008-11-10 796
-
ADL5385: 50 MHz至2200 MHz正交调制器2009-10-26 1270
-
ADRF6702-1200 MHz至2400 MHz正交调制器2011-11-17 801
-
LTC5589:700 MHz至6 GHz低功耗直接正交调制器数据表2021-05-15 549
-
LT5558:600 MHz至1100 MHz高线性直接正交调制器数据表2021-05-17 520
-
ADRF6720-27:集成小数N锁相环和压控振荡器的宽带正交调制器2021-05-18 874
-
基于MAX4454的I/Q发生器测试RF正交调制器2023-03-02 670
-
用基于MAX4454的I/Q发生器测试RF正交调制器2023-06-09 782
全部0条评论

快来发表一下你的评论吧 !

